一、提升方法基本模型
提升方法的基本思想是将多个学习器的结果进行适当的综合得到判断。这多个学习器多为弱学习器构成,因为弱学习器一般容易构造(比如,提升树算法中就以二叉树桩为弱分类器构造提升树),而组合这些弱学习器能构成一个强学习器。
提升方法面对的两个问题是:一,如何在每一轮改变数据的权重或概率分布;二,如何将弱学习器组合成一个强学习器。
第一个问题,AdaBoost的做法是,提高那些前一轮弱学习器错误学习的样本的权重,而降低那些被正确学习的样本的权重。那些没被正确学习的样本会受到更多的关注,在下一轮的学习中得到更多的调整。
第二个问题,AdaBoost采取加权多数表决的方法。加大学习误差率小的弱学习器的权重,使其在表决中起较大的作用。减小学习误差率大的弱分类器的权重,使其在表决中起较小的作用。
算法过程如下:
注意每个弱学习器的权重的构造,和每次对数据集权重更新的构造。


二、前向分步算法
因为提升方法模型弱学习器的加权加法模型,可以对其从前向后,每一步只学习一个基函数及其系数,逐步逼近目标函数,那么可以简化优化的复杂度。

三、提升树
提升树是以分类树或回归树为基本学习器的提升方法。提升树被认为是统计学习中性能最好的方法之一。其使用的基函数为二叉分类树或二叉回归树。
在一般提升方法中,m步损失函数计算的时候,都是直接以前m-1步已经得到的基函数线性组合fm-1(x),及m步的基函数的线性组合预测目标值y的损失计算。而在提升树模型中,把计算y与fm-1(x)的残差,作为m步的预测目标值。
算法如下:


四、GBDT
而GBDT在提升树的基础又做了一些改进,m步计算中,以损失函数的负梯度值作为回归提升树算法中残差的近似值,来拟合一个回归树。
为什么要这么替换,起先理解起来觉得负梯度替换残差很奇怪,但是考虑梯度(导数)最原始的定义不就是目标值的差比上自变量的差,而此处的残差就是在算m-1步目标值的差,所以GBDT中使用负梯度替换残差的目的,不仅是要找到残差为零的最优目标函数(提升树),而且还要尽快找到(沿着负梯度最陡峭的方向)。另外一种理解,可以考虑GBDT的优化方向就是找到梯度为0的点(局部最优点),而一般提升树的优化方向是残差为0的点,所以m步的优化目标函数换成损失函数的负梯度,就很好理解了。
算法如下:

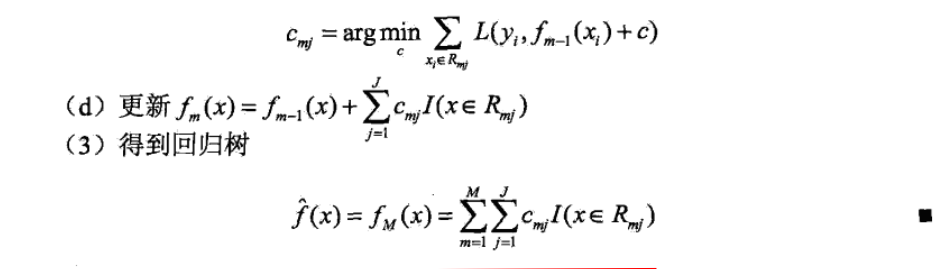
五、Xgboost