Fractal Streets
| Time Limit: 1000MS | Memory Limit: 65536K | |
| Total Submissions: 445 | Accepted: 162 |
Description
With a growing desire for modernization in our increasingly larger cities comes a need for new street designs. Chris is one of the unfortunate city planners responsible for these designs. Each year the demands keep increasing, and this year he has even been asked to design a completely new city.
More work is not something Chris needs right now, since like any good bureaucrat, he is extremely lazy. Given that this is a character trait he has in common with most computer scientists it should come as no surprise that one of his closest friends, Paul, is in fact a computer scientist. And it was Paul who suggested the brilliant idea that has made Chris a hero among his peers: Fractal Streets! By using a Hilbert curve, he can easily fill in rectangular plots of arbitrary size with very little work.
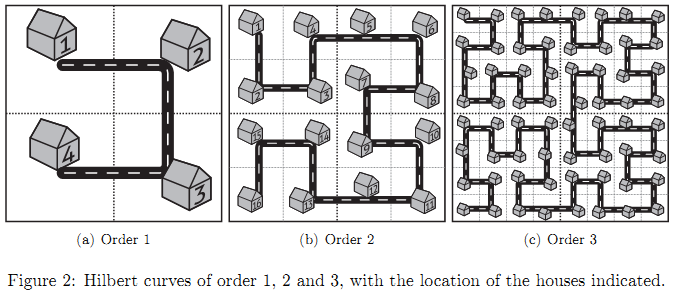
A Hilbert curve of order 1 consists of one "cup". In a Hilbert curve of order 2 that cup is replaced by four smaller but identical cups and three connecting roads. In a Hilbert curve of order 3 those four cups are in turn replaced by four identical but still smaller cups and three connecting roads, etc. At each corner of a cup a driveway (with mailbox) is placed for a house, with a simple successive numbering. The house in the top left corner has number 1, and the distance between two adjacent houses is 10m.
The situation is shown graphically in figure 2. As you can see the Fractal Streets concept successfully eliminates the need for boring street grids, while still requiring very little effort from our bureaucrats.
As a token of their gratitude, several mayors have offered Chris a house in one of the many new neighborhoods built with his own new scheme. Chris would now like to know which of these offerings will get him a house closest to the local city planning office (of course each of these new neighborhoods has one). Luckily he will not have to actually drive along the street, because his new company "car" is one of those new flying cars. This high-tech vehicle allows him to travel in a straight line from his driveway to the driveway of his new office. Can you write a program to determine the distance he will have to fly for each offier (excluding the vertical distance at takeoff and landing)?
More work is not something Chris needs right now, since like any good bureaucrat, he is extremely lazy. Given that this is a character trait he has in common with most computer scientists it should come as no surprise that one of his closest friends, Paul, is in fact a computer scientist. And it was Paul who suggested the brilliant idea that has made Chris a hero among his peers: Fractal Streets! By using a Hilbert curve, he can easily fill in rectangular plots of arbitrary size with very little work.
A Hilbert curve of order 1 consists of one "cup". In a Hilbert curve of order 2 that cup is replaced by four smaller but identical cups and three connecting roads. In a Hilbert curve of order 3 those four cups are in turn replaced by four identical but still smaller cups and three connecting roads, etc. At each corner of a cup a driveway (with mailbox) is placed for a house, with a simple successive numbering. The house in the top left corner has number 1, and the distance between two adjacent houses is 10m.
The situation is shown graphically in figure 2. As you can see the Fractal Streets concept successfully eliminates the need for boring street grids, while still requiring very little effort from our bureaucrats.

As a token of their gratitude, several mayors have offered Chris a house in one of the many new neighborhoods built with his own new scheme. Chris would now like to know which of these offerings will get him a house closest to the local city planning office (of course each of these new neighborhoods has one). Luckily he will not have to actually drive along the street, because his new company "car" is one of those new flying cars. This high-tech vehicle allows him to travel in a straight line from his driveway to the driveway of his new office. Can you write a program to determine the distance he will have to fly for each offier (excluding the vertical distance at takeoff and landing)?
Input
On the first line of the input is a positive integer, the number of test cases. Then for each test case:
A line containing a three positive integers, n < 16 and h, o < 231, specifying the order of the Hilbert curve, and the house numbers of the offered house and the local city planning office.
A line containing a three positive integers, n < 16 and h, o < 231, specifying the order of the Hilbert curve, and the house numbers of the offered house and the local city planning office.
Output
For each test case:
One line containing the distance Chris will have to fly to his work in meters, rounded to the nearest integer.
One line containing the distance Chris will have to fly to his work in meters, rounded to the nearest integer.
Sample Input
3 1 1 2 2 16 1 3 4 33
Sample Output
10 30 50
Source
丁队长告诉我们,心情不好的时候就要做做这种题
李煜东题解(侵删):
关键是要解决calc(N,P,M) :求编号为M的房屋在旋转P度的N级城市中的位置(P=0,90,180或270,逆时针为正方向)。本题就是求calc(N,0,S)与calc(N,0,D)的距离。
记一个旋转P度的N级城市为city(N,P)。当N>1时,该城市由四部分组成,左上是city(N-1,P-90),左下是city(N-1,P+90),右上和右下是city(N-1,P)。
已知N与P后很容易算出该城市道路依次经过其四个部分的顺序,通过M在1~22N四等分的大小位置可以确定M位于哪一部分(记为P’)。把之前经过的几个部分的房屋数量从M中减去(记为M’),然后递归求解calc(N-1,P’,M’)即可。

1 #include <iostream> 2 #include <cstdio> 3 #include <cstring> 4 #include <cstdlib> 5 #include <cmath> 6 7 inline void read(long long &x) 8 { 9 x = 0;char ch = getchar(),c = ch; 10 while(ch < '0' || ch > '9')c = ch, ch = getchar(); 11 while(ch <= '9' && ch >= '0')x = x * 10 + ch - '0', ch = getchar(); 12 if(c == '-')x = -x; 13 } 14 15 16 const long long INF = 0x3f3f3f3f; 17 18 long long t, N, S, D, pow4[40], pow2[40]; 19 20 struct Node 21 { 22 long long x, y; 23 Node(long long _x, long long _y){x = _x,y = _y;} 24 Node(){} 25 }; 26 27 //求解编号为m的房子,在逆时针旋转p度后的n级城市中的坐标 28 //p只能取值0,90,270 29 //90,270编号反转,0不变 30 31 Node cal(long long n, long long p, long long m) 32 { 33 if(n == 1) 34 { 35 if(p == 0) 36 { 37 if(m == 1)return Node(0,0); 38 else if(m == 2) return Node(0,1); 39 else if(m == 3) return Node(1,1); 40 else return Node(1,0); 41 } 42 else if(p == 90) 43 { 44 if(m == 3)return Node(0,0); 45 else if(m == 2) return Node(0,1); 46 else if(m == 1) return Node(1,1); 47 else return Node(1,0); 48 } 49 else if(p == 270) 50 { 51 if(m == 1)return Node(0,0); 52 else if(m == 4) return Node(0,1); 53 else if(m == 3) return Node(1,1); 54 else return Node(1,0); 55 } 56 else if(p == 180) 57 { 58 if(m == 3)return Node(0,0); 59 else if(m == 4) return Node(0,1); 60 else if(m == 1) return Node(1,1); 61 else return Node(1,0); 62 } 63 } 64 Node tmp; 65 long long a = pow4[n - 1]; 66 long long r = (m - 1) / a + 1; 67 if(p == 0) 68 { 69 if(r == 1) tmp = cal(n - 1, 270, m); 70 else if(r == 2) tmp = cal(n - 1, 0, m - a), tmp.y += pow2[n - 1]; 71 else if(r == 3) tmp = cal(n - 1, 0, m - 2 * a), tmp.x += pow2[n - 1], tmp.y += pow2[n - 1]; 72 else tmp = cal(n - 1, 90, m - a * 3), tmp.x += pow2[n - 1]; 73 } 74 else if(p == 90) 75 { 76 if(r == 1) tmp = cal(n - 1, 180, m), tmp.x += pow2[n - 1], tmp.y += pow2[n - 1]; 77 else if(r == 2) tmp = cal(n - 1, 90, m - a), tmp.y += pow2[n - 1]; 78 else if(r == 3) tmp = cal(n - 1, 90, m - a * 2); 79 else tmp = cal(n - 1, 0, m - a * 3), tmp.x += pow2[n - 1]; 80 } 81 else if(p == 270) 82 { 83 if(r == 1) tmp = cal(n - 1, 0, m); 84 else if(r == 2) tmp = cal(n - 1, 270, m - a), tmp.x += pow2[n - 1]; 85 else if(r == 3) tmp = cal(n - 1, 270, m - 2 * a), tmp.x += pow2[n - 1], tmp.y += pow2[n - 1]; 86 else tmp = cal(n - 1, 180, m - 3 * a), tmp.y += pow2[n - 1]; 87 } 88 else if(p == 180) 89 { 90 if(r == 1) tmp = cal(n - 1, 90, m), tmp.x += pow2[n - 1], tmp.y += pow2[n - 1]; 91 else if(r == 2) tmp = cal(n - 1, 180, m - a), tmp.x += pow2[n - 1]; 92 else if(r == 3) tmp = cal(n - 1, 180, m - a * 2); 93 else tmp = cal(n - 1, 270, m - a * 3), tmp.y += pow2[n - 1]; 94 } 95 return tmp; 96 } 97 98 int main() 99 { 100 //freopen("data.txt", "r" ,stdin); 101 read(t); 102 pow4[0] = 1, pow2[0] = 1; 103 for(register int i = 1;i <= 33;++ i) pow4[i] = (pow4[i - 1] << 2), pow2[i] = (pow2[i - 1] << 1); 104 Node tmp1, tmp2; 105 for(;t;-- t) 106 { 107 read(N),read(S),read(D); 108 tmp1 = cal(N, 0, S); 109 tmp2 = cal(N, 0, D); 110 double len = sqrt((long long)abs(tmp1.x - tmp2.x) * abs(tmp1.x - tmp2.x) + (long long)abs(tmp1.y - tmp2.y) * abs(tmp1.y - tmp2.y)) * 10; 111 printf("%lld ", (long long)(len + 0.5)); 112 } 113 return 0; 114 }
