本文源于《An Introduction to Deep Learning: From Perceptrons to Deep Networks》作者对于例子的选择、理论的介绍都很到位,由浅入深
感知机最早的监督式训练算法,是神经网络构建的基础。找出平面上的一条线来将不同标记的数据点分开(如图)
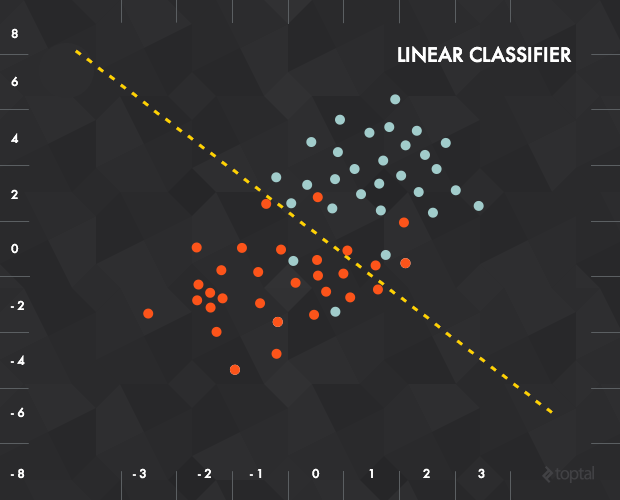
f(x)=wx+b ,调整权重w和b
缺陷:只能学习线性可分函数。这个缺陷重要吗?比如 XOR,这么简单的函数,都不能被线性分类器分类(如下图所示,分隔两类点失败):

多层感知机-前馈神经网络:
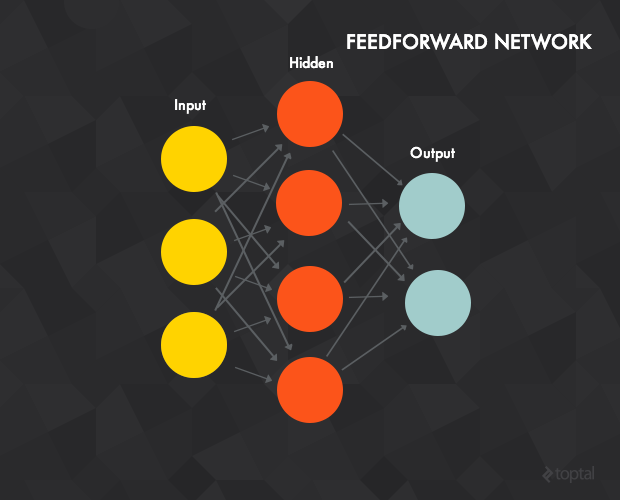
具有以下特点
- 一个输入层,一个输出层,一个或多个隐含层
- 每一个神经元都是一个上文提到的感知机。
- 在 t 层的每个神经元通常与前一层( t - 1层)中的每个神经元都有连接(但你可以通过将这条连接的权重设为0来断开这条连接)
如果每一个感知机都只能使用一个线性激活函数会怎么样?整个网络的最终输出也仍然是将输入数据通过一些线性函数计算过一遍,只是用一些在网络中收集的不同权值调整了一下。换名话说,再多线性函数的组合还是线性函数。如果我们限定只能使用线性激活函数的话,前馈神经网络其实比一个感知机强大不到哪里去,无论网络有多少层。正是这个原因,大多数神经网络都是使用的非线性激活函数,如对数函数、双曲正切函数、阶跃函数、整流函数等。不用这些非线性函数的神经网络只能学习输入数据的线性组合。
训练
大多数常见的应用在多层感知机的监督式训练的算法都是反向传播算法。
1、将训练样本通过神经网络进行前向传播计算。
2、计算输出误差,常用均方差:

其中 t 是目标值, y 是实际的神经网络计算输出。其它的误差计算方法也可以,但MSE(均方差)通常是一种较好的选择。
3、网络误差通过随机梯度下降的方法来最小化。
隐含层
根据普适逼近原理,一个具有有限数目神经元的隐含层可以被训练成可逼近任意随机函数。
隐含层存储了训练数据的内在抽象表示,和人类大脑(简化的类比)保存有对真实世界的抽象一样。接下来,我们将用各种方法来搞一下这个隐含层。
大规模网络中的难题
神经网络中可以有多个隐含层:这样,在更高的隐含层里可以对其之前的隐含层构建新的抽象。而且像之前也提到的,这样可以更好的学习大规模网络。增加隐含层的层数通常会导致两个问题:
1、梯度消失:随着我们添加越来越多的隐含层,反向传播传递给较低层的信息会越来越少。实际上,由于信息向前反馈,不同层次间的梯度开始消失,对网络中权重的影响也会变小。
2、过度拟合:也许这是机器学习的核心难题。简要来说,过度拟合指的是对训练数据有着过于好的识别效果,这时导至模型非常复杂。这样的结果会导致对训练数据有非常好的识别较果,而对真实样本的识别效果非常差。
自编码器
自编码器就是一个典型的前馈神经网络,它的目标就是学习一种对数据集的压缩且分布式的表示方法(编码思想)。

从概念上讲,神经网络的目的是要训练去“重新建立”输入数据,好像输入和目标输出数据是一样的。换句话说:你正在让神经网络的输出与输入是同一样东西,只是经过了压缩。
在这样的算法架构背后,神经网络学习到的实际上并不是一个训练数据到标记的“映射”,而是去学习数据本身的内在结构和特征(也正是因为这,隐含层也被称作特征探测器(feature detector))。通常隐含层中的神经元数目要比输入/输入层的少,这是为了使神经网络只去学习最重要的特征并实现特征的降维
受限波尔兹曼机
一种可以在输入数据集上学习概率分布的生成随机神经网络。
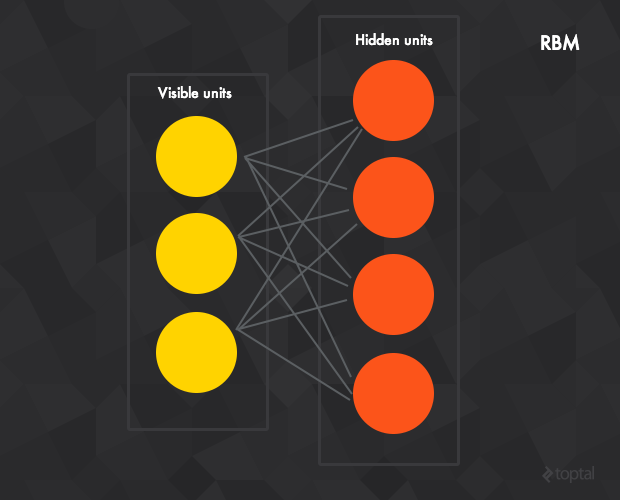
RBM由隐含层、可见层、偏置层组成。和前馈神经网络不同,可见层和隐含层之间的连接是无方向性(值可以从可见层->隐含层或隐含层->可见层任意传输)且全连接的(每一个当前层的神经元与下一层的每个神经元都有连接——如果允许任意层的任意神经元连接到任意层去,我们就得到了一个波尔兹曼机(非受限的))。最近出现的对比差异无监督训练算法使这个领域复兴。
对比差异
单步对比差异算法原理:
1、正向过程:
-
- 输入样本 v 输入至输入层中。
- v 通过一种与前馈网络相似的方法传播到隐含层中,隐含层的激活值为 h。
2、反向过程:
-
- 将 h 传回可见层得到 v’ (可见层和隐含层的连接是无方向的,可以这样传)。
- 再将 v’ 传到隐含层中,得到 h’。
3、权重更新:
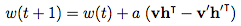
其中 a 是学习速率, v, v’, h, h’ 和 w 都是向量。
这其中的主要的思想:在正向过程中影响了网络的内部对于真实数据的表示。同时,反向过程中尝试通过这个被影响过的表示方法重建数据。主要目的是可以使生成的数据与原数据尽可能相似,这个差异影响了权重更新。
换句话说,这样的网络具有了感知对输入数据表示的程度的能力,而且尝试通过这个感知能力重建数据。如果重建出来的数据与原数据差异很大,那么进行调整并再次重建。
深度网络
已经发现这些结构可以通过栈式叠加来实现深度网络。这些网络可以通过贪心法的思想训练,每次训练一层,以克服之前提到在反向传播中梯度消失及过度拟合的问题。
栈式自编码器
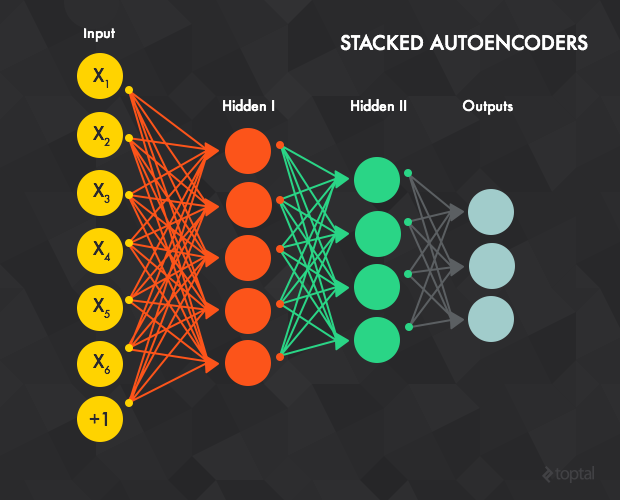
自编码器的隐含层 t 会作为 t + 1 层的输入层。第一个输入层就是整个网络的输入层。利用贪心法训练每一层的步骤如下:
1、通过反向传播的方法利用所有数据对第一层的自编码器进行训练(t=1,上图中的红色连接部分)。(自编码本身就相当于是一个有监督学习的过程)
2、训练第二层的自编码器 t=2 (绿色连接部分)。由于 t=2 的输入层是 t=1 的隐含层,我们已经不再关心 t=1 的输入层,可以从整个网络中移除。整个训练开始于将输入样本数据赋到 t=1 的输入层,通过前向传播至 t = 2 的输出层。下面t = 2的权重(输入->隐含和隐含->输出)使用反向传播的方法进行更新。t = 2的层和 t=1 的层一样,都要通过所有样本的训练。(栈式或者相当于阶梯式的,上了一层就不管下一层是怎样的到的)
3、对所有层重复步骤1-2(即移除前面自编码器的输出层,用另一个自编码器替代,再用反向传播进行训练)。
4、步骤1-3被称为预训练,这将网络里的权重值初始化至一个合适的位置。但是通过这个训练并没有得到一个输入数据到输出标记的映射。例如,一个网络的目标是被训练用来识别手写数字,经过这样的训练后还不能将最后的特征探测器的输出(即隐含层中最后的自编码器)对应到图片的标记上去。这样,一个通常的办法是在网络的最后一层(即蓝色连接部分)后面再加一个或多个全连接层。整个网络可以被看作是一个多层的感知机,并使用反向传播的方法进行训练(这步也被称为微调)。
栈式自编码器,提供了一种有效的预训练方法来初始化网络的权重,这样你得到了一个可以用来训练的复杂、多层的感知机。
深度信度网络
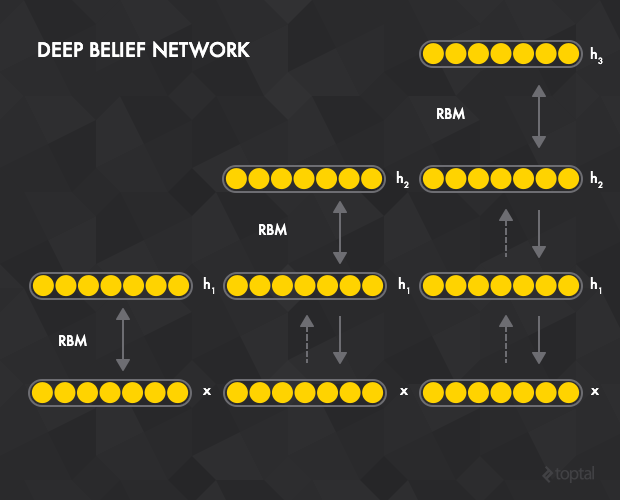
在本例中,隐含层 RBM t 可以看作是 RBM t+1 的可见层。第一个RBM的输入层即是整个网络的输入层,层间贪心式的预训练的工作模式如下:
1. 通过对比差异法对所有训练样本训练第一个RBM t=1
2. 训练第二个RBM t=1。由于 t=2 的可见层是 t=1 的隐含层,训练开始于将数据赋至 t=1 的可见层,通过前向传播的方法传至 t=1 的隐含层。然后作为 t=2 的对比差异训练的初始数据。
3. 对所有层重复前面的过程。
4. 和栈式自编码器一样,通过预训练后,网络可以通过连接到一个或多个层间全连接的 RBM 隐含层进行扩展。这构成了一个可以通过反向传僠进行微调的多层感知机。
本过程和栈式自编码器很相似,只是用RBM将自编码器进行替换,并用对比差异算法将反向传播进行替换。
(注: 例中的源码可以从 此处获得.)
卷积网络
这个是本文最后一个软件架构——卷积网络,一类特殊的对图像识别非常有效的前馈网络。
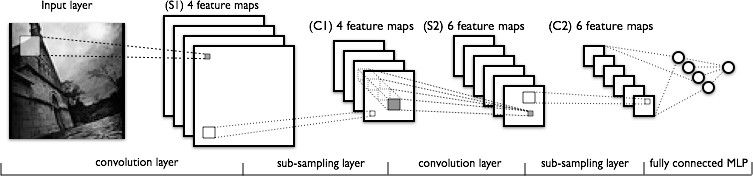
在我们深入看实际的卷积网络之臆,我们先定义一个图像滤波器,或者称为一个赋有相关权重的方阵。一个滤波器可以应用到整个图片上,通常可以应用多个滤波器。比如,你可以应用四个6x6的滤波器在一张图片上。然后,输出中坐标(1,1)的像素值就是输入图像左上角一个6x6区域的加权和,其它像素也是如此。
有了上面的基础,我们来介绍定义出卷积网络的属性:
- 卷积层 对输入数据应用若干滤波器。比如图像的第一卷积层使用4个6x6滤波器。对图像应用一个滤波器之后的得到的结果被称为特征图谱(feature map, FM),特征图谱的数目和滤波器的数目相等。如果前驱层也是一个卷积层,那么滤波器应用在FM上,相当于输入一个FM,输出另外一个FM。从直觉上来讲,如果将一个权重分布到整个图像上后,那么这个特征就和位置无关了,同时多个滤波器可以分别探测出不同的特征。
- 下采样层 缩减输入数据的规模。例如输入一个32x32的图像,并且通过一个2x2的下采样,那么可以得到一个16x16的输出图像,这意味着原图像上的四个像素合并成为输出图像中的一个像素。实现下采样的方法有很多种,最常见的是最大值合并、平均值合并以及随机合并。
- 最后一个下采样层(或卷积层)通常连接到一个或多个全连层,全连层的输出就是最终的输出。
- 训练过程通过改进的反向传播实现,将下采样层作为考虑的因素并基于所有值来更新卷积滤波器的权重。