洛谷P1712 [NOI2016]区间

题目描述

在数轴上有 $N$ 个闭区间 $[l_1,r_1],[l_2,r_2],...,[l_n,r_n]$ 。现在要从中选出 $M$ 个区间，使得这 $M$ 个区间共同包含至少一个位置。换句话说，就是使得存在一个 $x$ ，使得对于每一个被选中的区间 $[l_i,r_i]$ ，都有 $l_i≤x≤r_i$ 。

对于一个合法的选取方案，它的花费为被选中的最长区间长度减去被选中的最短区间长度。区间 $[l_i,r_i]$ 的长度定义为 $r_i-l_i$ ，即等于它的右端点的值减去左端点的值。

求所有合法方案中最小的花费。如果不存在合法的方案，输出 $-1$ 。

输入输出格式

输入格式：

第一行包含两个正整数 $N,M$ 用空格隔开，意义如上文所述。保证 $1≤M≤N$

接下来 $N$ 行，每行表示一个区间，包含用空格隔开的两个整数 $l_i$ 和 $r_i$ 为该区间的左右端点。

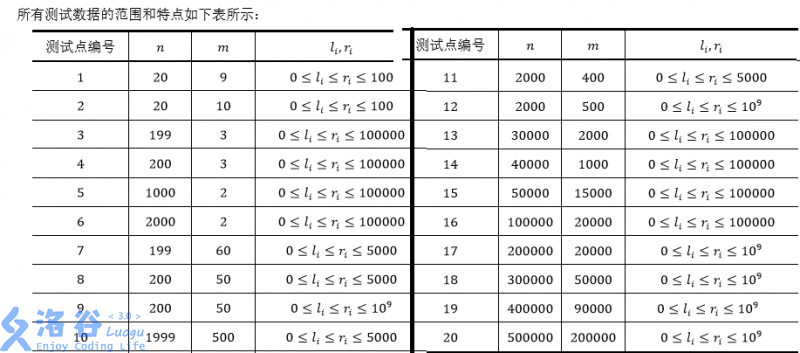
$N<=500000,M<=200000,0≤li≤ri≤10^9$

输出格式：

只有一行，包含一个正整数，即最小花费。

输入输出样例

输入样例#1： 复制

6 3
3 5
1 2
3 4
2 2
1 5
1 4

输出样例#1： 复制

2

说明

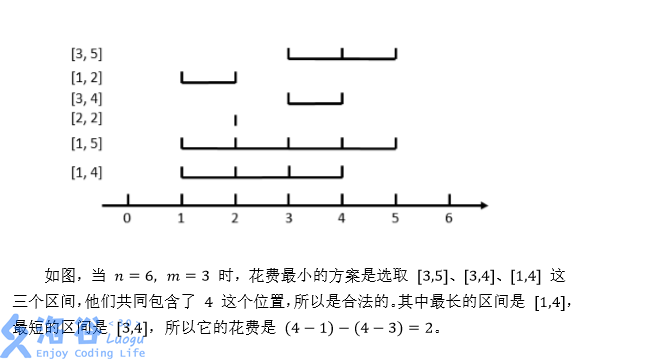
分析

代码

#include<bits/stdc++.h>
#define lson now<<1,l,mid
#define rson now<<1|1,mid+1,r
using namespace std;
const int N=1000010;
const int INF=0x7f7f7f7f;
int n,m,tot,top,c[N*2];
int x,y,k,ans,maxl[N*3],tag[N*3];
struct node{
    int x,y,len;
    bool operator < (const node &j) const{
        return len<j.len;
    }
}a[N];
inline void pushup(int now){
    maxl[now]=max(maxl[now<<1],maxl[now<<1|1]);
}
inline void pushdown(int now){
    int lc=now<<1,rc=now<<1|1;
    maxl[lc]+=tag[now]; maxl[rc]+=tag[now];
    tag[lc]+=tag[now]; tag[rc]+=tag[now];
    tag[now]=0;
}
void modify(int now,int l,int r){
    if(x<=l&&r<=y){
        tag[now]+=k; maxl[now]+=k;
        return;
    }
    if(tag[now]) pushdown(now);
    int mid=(l+r)>>1;
    if(x<=mid) modify(lson);
    if(y>mid) modify(rson);
    pushup(now);
}
int main(){
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;++i){
        scanf("%d%d",&a[i].x,&a[i].y);
        a[i].len=a[i].y-a[i].x;
        c[++tot]=a[i].x; c[++tot]=a[i].y;
    }
    top=0; ans=INF;
    sort(c+1,c+tot+1);
    tot=unique(c+1,c+tot+1)-c-1;
    for(int i=1;i<=n;++i){
        a[i].x=lower_bound(c+1,c+tot+1,a[i].x)-c;
        a[i].y=lower_bound(c+1,c+tot+1,a[i].y)-c;
    }
    sort(a+1,a+n+1);
    for(int i=1;i<=n;i++) {
        while(maxl[1]<m&&top<n){
            top++;
            x=a[top].x; y=a[top].y; k=1;
            modify(1,1,tot);
        }
        if(maxl[1]==m) ans=min(ans,a[top].len-a[i].len);
        x=a[i].x; y=a[i].y; k=-1;
        modify(1,1,tot);
    }
    if(ans==INF) printf("-1");
    else printf("%d",ans);
}