CF916E Jamie and Tree 题解

参考博文

题目大意：

有一棵(n)个节点的有根树，标号为(1-n)，你需要维护以下三种操作

1.给定一个点(v)，将整颗树的根变为(v)

2.给定两个点(u), (v)，将(lca(u, v))所在的子树都加上(x)

3.给定一个点(v)，你需要回答以v所在的子树的权值和

分析：

我们要写一个数据结构，支持换根，子树修改，子树查询，找最近公共祖先

先以(1)为根进行一遍树剖

接着逐个分析qaq

1.换根

直接换掉，没什么好说的

2.子树修改

我们要分类讨论，为了叙述方便，记(x,y)在原树中的(LCA)为(lca(x,y))

对于任意一点x，有以下几种情况：

((1)x=root)，修改整棵树

((2)lca(x,root)!=x)，那么换根不影响子树，直接修改

((3)lca(x,root)=x)，可以画图证明(x)的子树就是(x)原有的子树减去(x)的(root)所在的一个“树枝”，所以我们先修改整棵树，在将(root)所在的树枝还原

3.LCA

我们不妨默认(dep[x]leq dep[y])

进行分类讨论：

((1)lca(x,y)=x)

(1)root)在(y)的子树中，那么答案为(y)

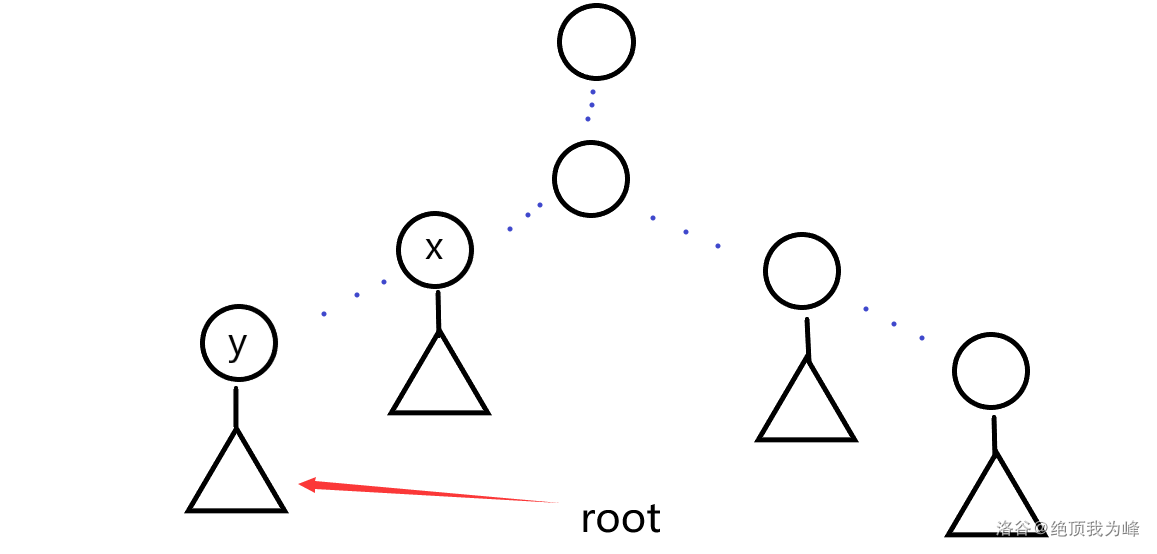
(2)root)在(x)与(y)之间，那么答案为(root)

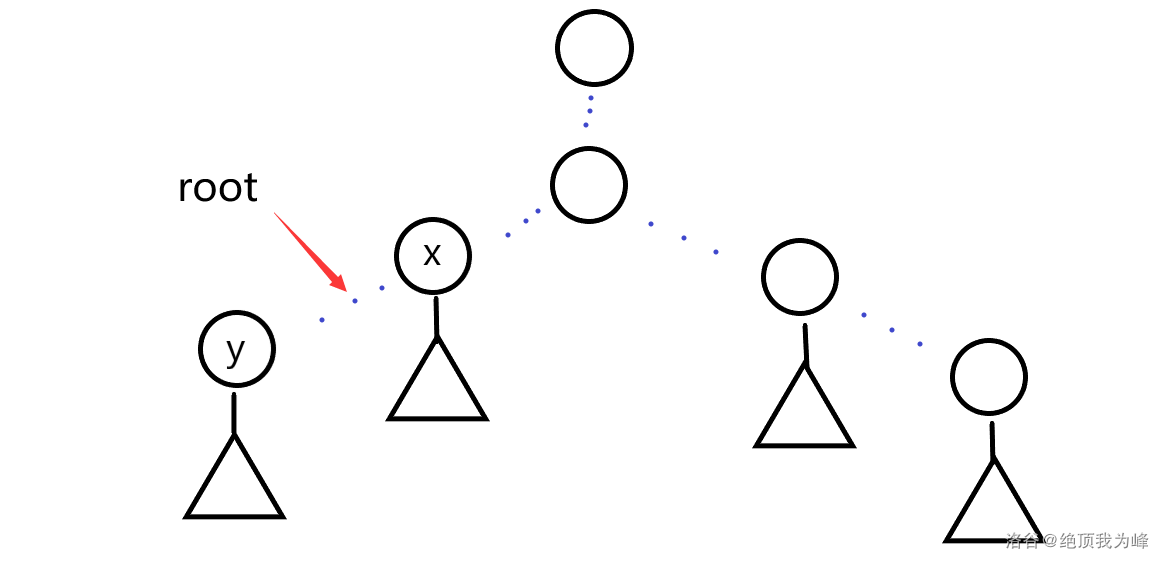
(3)root)在其他位置，那么答案为(x)

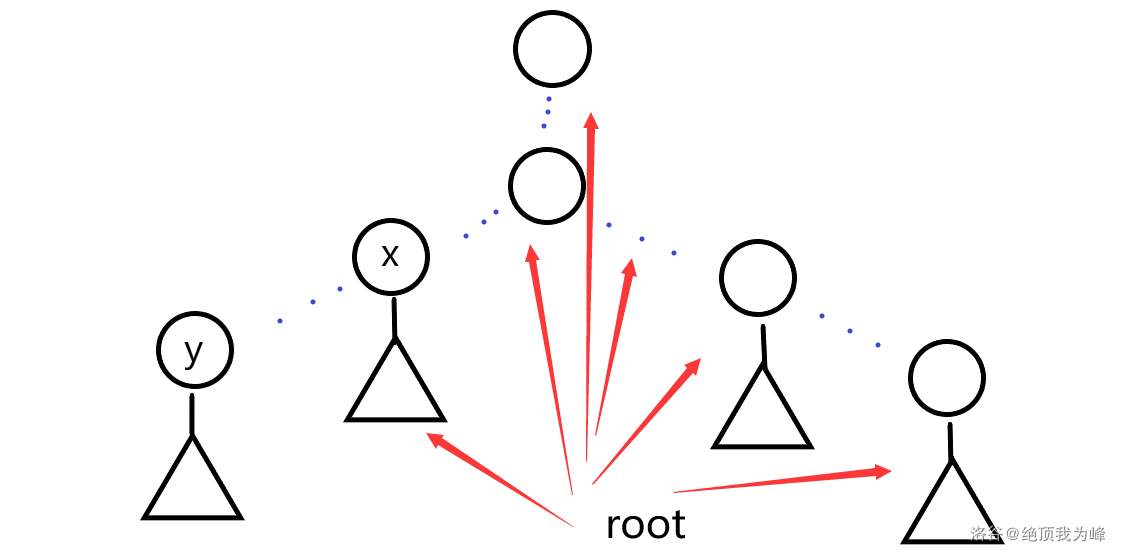
((2)lca(x,y)!=x)

(1)root)在(x)的子树中，那么答案为(x)

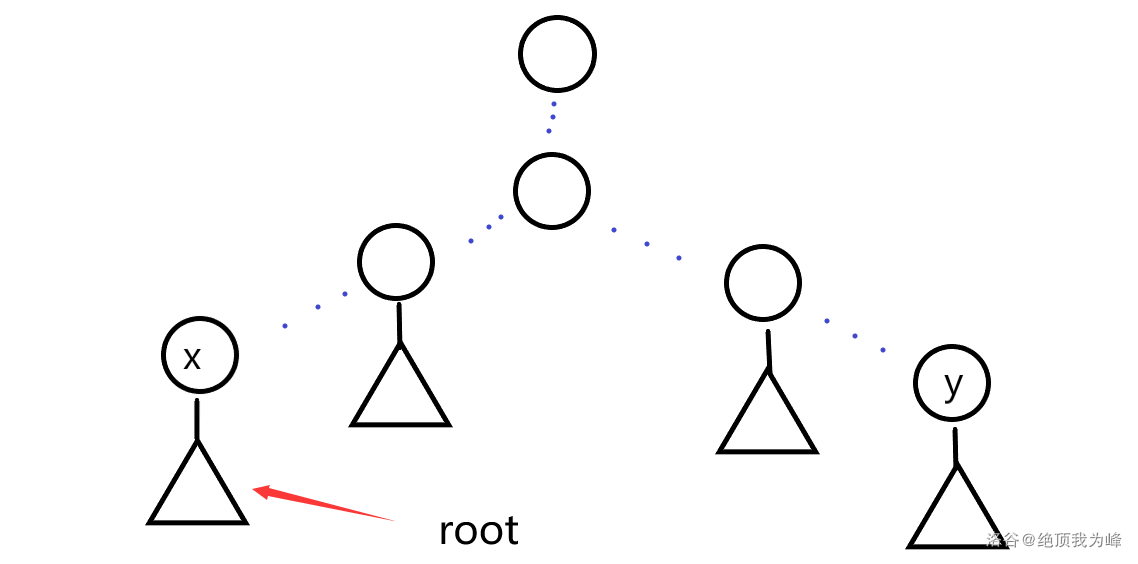
(2)root)在(y)的子树中，那么答案为(y)

(3)root)在(x)到(y)的路径上，那么答案为(root)

(4))若(lca(x,root)=lca(y,root))，即(root)在下图所示位置，答案为(lca(x,y))

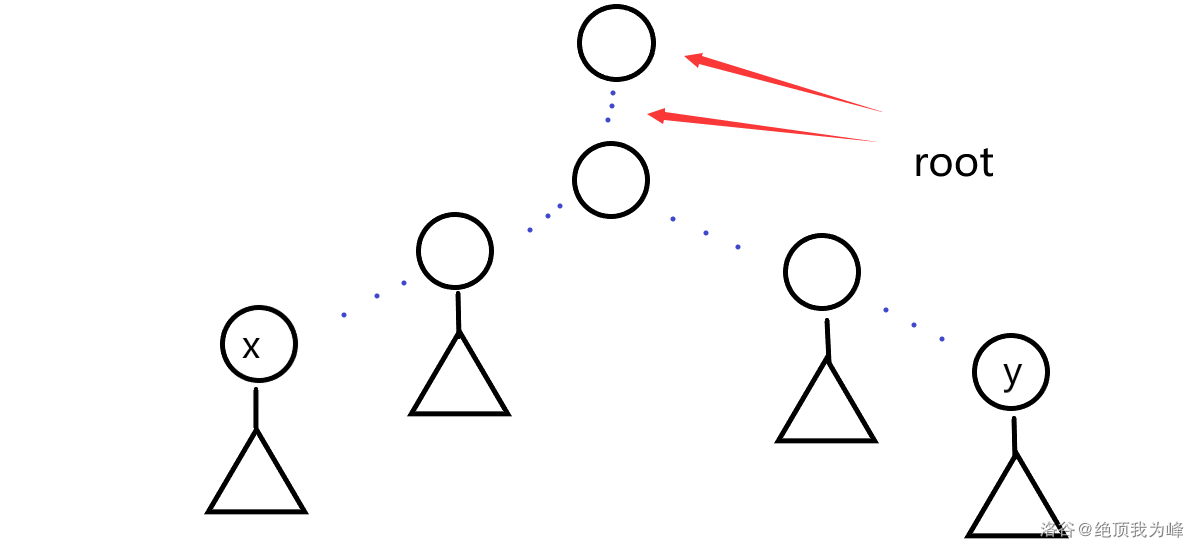
(5))若(lca(x,y)!=lca(x,root))，即(root)在下图位置，答案为(lca(x,root))

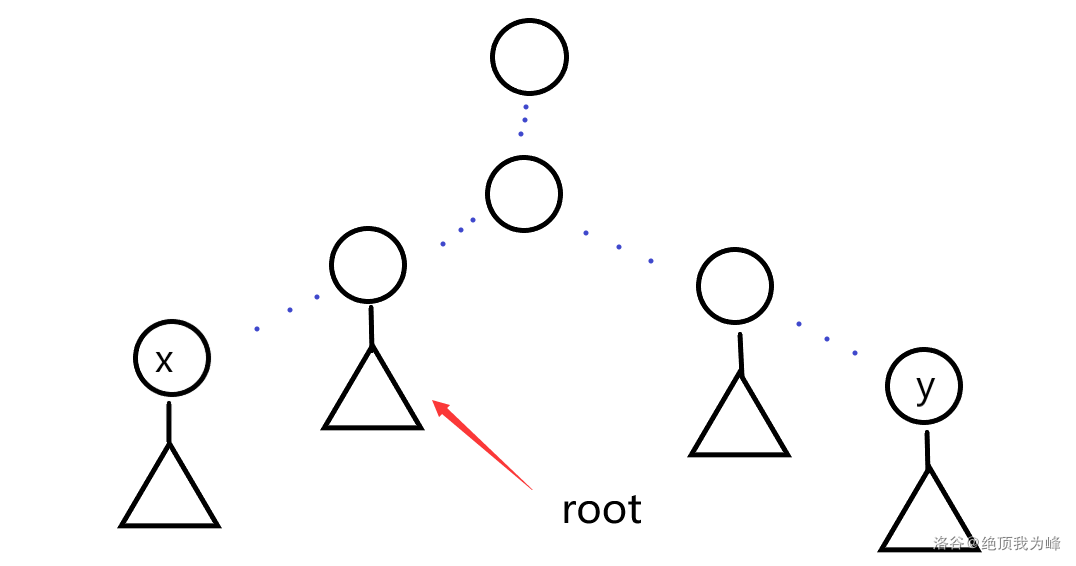
(6))若(lca(x,y)!=lca(y,root))，即(root)在下图位置，答案为(lca(y,root))

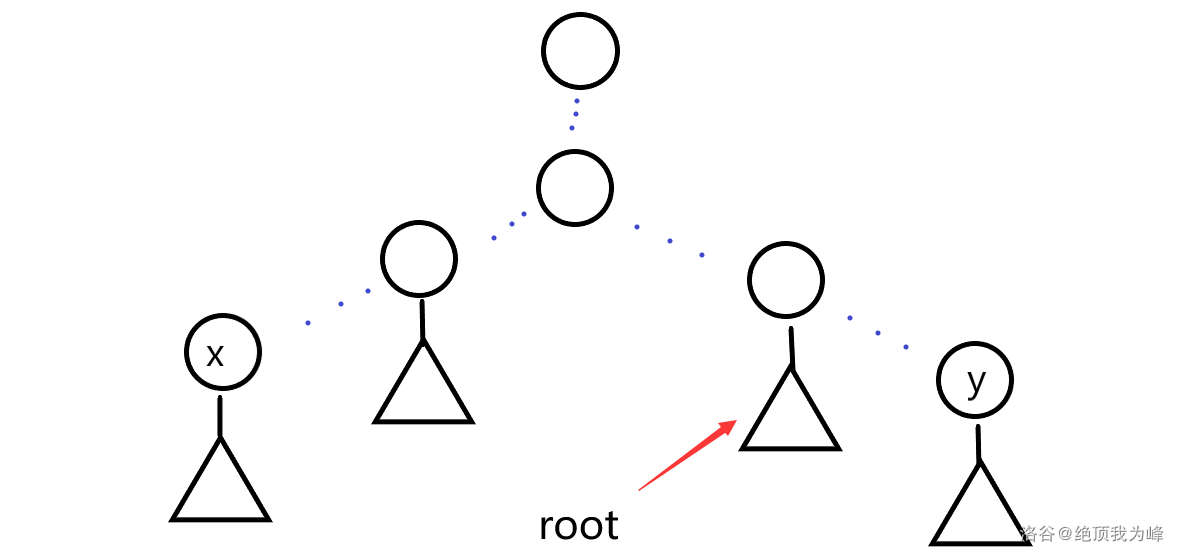
4.子树查询

同2

#include <bits/stdc++.h>
#define int long long
#define ls o<<1
#define rs o<<1|1
using namespace std ;
const int MAXN = 300005 ;
struct Node {
    int next , to ;
} edge[ MAXN << 1 ] ;
int head[ MAXN ] , cnt ;
int root , n , m , r , tot ;
int a[ MAXN ] , dep[ MAXN ] , fa[ MAXN ] , siz[ MAXN ] , son[ MAXN ] , id[ MAXN ] , w[ MAXN ] , top[ MAXN ] ;
int ans[ MAXN << 2 ] , tag[ MAXN << 2 ] ;
inline int read ()  {
    int tot = 0 , f = 1 ; char c = getchar () ;
    while ( c < '0' || c > '9' ) { if ( c == '-' ) f = -1 ; c = getchar () ; }
    while ( c >= '0' && c <= '9' ) { tot = tot * 10 + c - '0' ; c = getchar () ; }
    return tot * f ;
}
inline void add ( int x , int y ) {
    edge[ ++ cnt ].next = head[ x ] ;
    edge[ cnt ].to = y ;
    head[ x ] = cnt ;
}
inline void pushup ( int o ) { ans[ o ] = ans[ ls ] + ans[ rs ] ; }
inline void pushdown ( int o , int l , int r ) {
    if ( tag[ o ] == 0 ) return ;
    int mid = ( l + r ) >> 1 ;
    ans[ ls ] += tag[ o ] * ( mid - l + 1 ) ;
    ans[ rs ] += tag[ o ] * ( r - mid ) ;
    tag[ ls ] += tag[ o ] ; tag[ rs ] += tag[ o ] ;
    tag[ o ] = 0 ;
}
inline void build ( int o , int l , int r ) {
    if ( l == r ) {
        ans[ o ] = w[ l ] ;
        return ;
    }
    int mid = ( l + r ) >> 1 ;
    build ( ls , l , mid ) ;
    build ( rs , mid + 1 , r ) ;
    pushup ( o ) ;
}
inline void update ( int o , int l , int r , int nl , int nr , int p ) {
    if ( l >= nl && r <= nr ) {
        ans[ o ] += p * ( r - l + 1 ) ;
        tag[ o ] += p ;
        return ;
    }
    pushdown ( o , l , r ) ;
    int mid = ( l + r ) >> 1 ;
    if ( nl <= mid ) update ( ls , l , mid , nl , nr , p ) ;
    if ( nr > mid ) update ( rs , mid + 1 , r , nl , nr , p ) ;
    pushup ( o ) ;
}
inline int query ( int o , int l , int r , int nl , int nr ) {
    if ( l >= nl && r <= nr ) return ans[ o ] ;
    pushdown ( o , l , r ) ;
    int mid = ( l + r ) >> 1 ;
    int res = 0 ;
    if ( nl <= mid ) res += query ( ls , l , mid , nl , nr ) ;
    if ( nr > mid ) res += query ( rs , mid + 1 , r , nl , nr ) ;
    return res ;
}
inline void dfs1 ( int u , int f , int deep ) {
    dep[ u ] = deep ;
    fa[ u ] = f ;
    siz[ u ] = 1 ;
    for ( int i = head[ u ] ; i ; i = edge[ i ].next ) {
        int v = edge[ i ].to ;
        if ( v == f ) continue ;
        dfs1 ( v , u , deep + 1 ) ;
        siz[ u ] += siz[ v ] ;
        if ( siz[ v ] > siz[ son[ u ] ] || son[ u ] == 0 ) son[ u ] = v ;
    }
}
inline void dfs2 ( int u , int tp ) {
    id[ u ] = ++ tot ;
    w[ tot ] = a[ u ] ;
    top[ u ] = tp ;
    if ( !son[ u ] ) return ;
    dfs2 ( son[ u ] , tp ) ;
    for ( int i = head[ u ] ; i ; i = edge[ i ].next ) {
        int v = edge[ i ].to ;
        if ( v == fa[ u ] || v == son[ u ] ) continue ;
        dfs2 ( v , v ) ;
    }
}
inline int lca ( int x , int y ) {
    while ( top[ x ] != top[ y ] ) {
        if ( dep[ top[ x ] ] < dep[ top[ y ] ] ) swap ( x , y ) ;
        x = fa[ top[ x ] ] ;
    }
    if ( dep[ x ] > dep[ y ] ) swap ( x , y ) ;
    return x ;
}
inline int find ( int x , int y ) {
    while ( top[ x ] != top[ y ] ) {
        if ( dep[ top[ x ] ] < dep[ top[ y ] ] ) swap ( x , y ) ;
        if ( fa[ top[ x ] ] == y ) return top[ x ] ;
        x = fa[ top[ x ] ] ;
    }
    if ( dep[ x ] > dep[ y ] ) swap ( x , y ) ;
    return son[ x ] ;
}
inline int LCA ( int x , int y ) {
    if ( dep[ x ] > dep[ y ] ) swap ( x , y ) ;
    if ( lca ( x , y ) == x ) {
        if ( id[ root ] >= id[ y ] && id[ root ] <= id[ y ] + siz[ y ] - 1 ) return y ;
        if ( lca ( x , root ) == x ) return lca ( y , root ) ;
        return x ;
    }
    if ( id[ root ] >= id[ x ] && id[ root ] <= id[ x ] + siz[ x ] - 1 ) return x ;
    if ( id[ root ] >= id[ y ] && id[ root ] <= id[ y ] + siz[ y ] - 1 ) return y ;
    if ( ( lca ( x , root ) == root && lca ( x , y ) == lca ( y , root ) ) || ( lca ( y , root ) == root && lca ( x , y ) == lca ( x , root ) ) ) return root ;
    if ( lca ( x , root ) == lca ( y , root ) ) return lca ( x , y ) ;
    if ( lca ( x , y ) != lca ( x , root ) ) return lca ( x , root ) ;
    return lca ( y , root ) ;
}
inline void up2 ( int x , int p ) {
    if ( root == x ) {
        update ( 1 , 1 , n , 1 , n , p ) ;
        return ;
    }
    int tmp = lca ( root , x ) ;
    if ( tmp != x )
        update ( 1 , 1 , n , id[ x ] , id[ x ] + siz[ x ] - 1 , p ) ;
    else {
        int nod = find ( root , x ) ;
        update ( 1 , 1 , n , 1 , n , p ) ;
        update ( 1 , 1 , n , id[ nod ] , id[ nod ] + siz[ nod ] - 1 , -p ) ;
    }
}
inline int q2 ( int x ) {
    if ( x == root ) return query ( 1 , 1 , n , 1 , n ) ;
    int tmp = lca ( root , x ) ;
    if ( tmp != x )
        return query ( 1 , 1 , n , id[ x ] , id[ x ] + siz[ x ] - 1 ) ;
    int nod = find ( root , x ) ;
    return query ( 1 , 1 , n , 1 , n ) - query ( 1 , 1 , n , id[ nod ] , id[ nod ] + siz[ nod ] - 1 ) ;
}
signed main () {
    n = read () ; m = read () ; root = 1 ;
    for ( int i = 1 ; i <= n ; i ++ )
        a[ i ] = read () ;
    for ( int i = 1 ; i < n ; i ++ ) {
        int x = read () , y = read () ;
        add ( x , y ) ; add ( y , x ) ;
    }
    dfs1 ( 1 , 0 , 1 ) ;
    dfs2 ( 1 , 1 ) ;
    build ( 1 , 1 , n ) ;
    while ( m -- ) {
        int opt = read () ;
        if ( opt == 1 ) root = read () ;
        else if ( opt == 2 ) {
            int x = read () , y = read () , z = read () ;
            up2 ( LCA ( x , y ) , z ) ;
        }
        else {
            int x = read () ;
            printf ( "%lld
" , q2 ( x ) ) ;
        }
    }
    return 0 ;
}