1、非对称加密过程:
假如现实世界中存在A和B进行通讯,为了实现在非安全的通讯通道上实现信息的保密性、完整性、可用性(即信息安全的三个性质),A和B约定使用非对称加密通道进行通讯,具体过程如下:
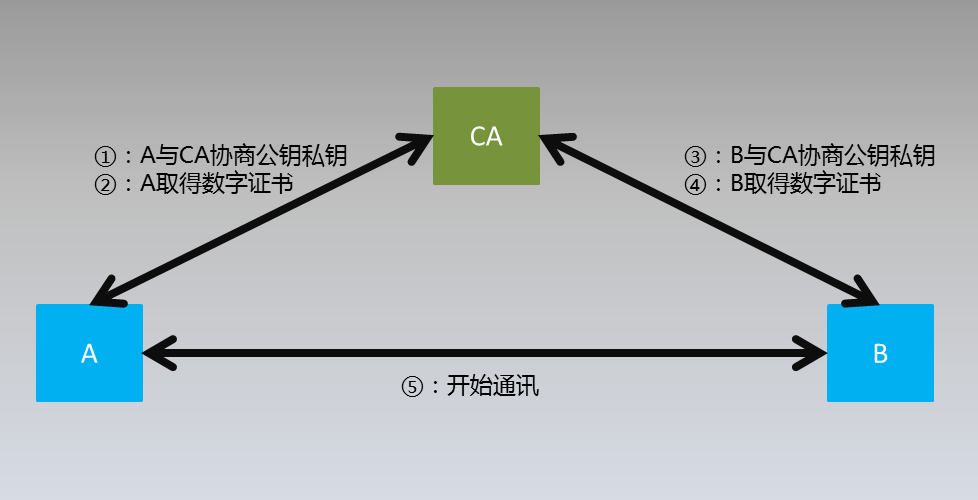
说明:
国内目前使用双证书体系,即用户同时拥有签名证书、加密证书两张证书。签名证书是用户的身份认证,是和CA协商的结果,可用于对用户A的身份验证;加密证书是用来对信息进行加密,是用户和秘钥管理系统生成。我们在这里假设都适合CA进行交互。
①:此过程是生成公钥私钥的过程,我们这里基于RSA算法实现,RSA算法的详细说明在后面讲解。
②:此过程是CA对用户的身份进行签名,目的验证A的身份。这样在A与B通讯的过程中,A可以把自己的数字签名发给B,B得到此数字签名后就可以通过CA的公钥对其进行解密并进行身份验证,具体过程在后面讲解。
③④同理。
⑤:A对要传输的信息进行加密并传输,B接受到以后进行解密的过程。
2、RSA算法:
RSA原理:RSA算法基于一个十分简单的数论事实:将两个大素数相乘十分容易,但是想要对其乘积进行因式分解却极其困难,因此可以将乘积公开作为加密密钥。
算法:
(1)选择两个不同的大素数p和q;
(2)计算乘积n=pq和Φ(n)=(p-1)(q-1);
(3)选择大于1小于Φ(n)的随机整数e,使得gcd(e,Φ(n))=1;注:gcd即最大公约数。
(4)计算d使得d*e=1mod Φ(n);注:即d*e mod Φ(n) =1。
(5)对每一个密钥k=(n,p,q,d,e),定义加密变换为Ek(x)=xe mod n,解密变换为Dk(x)=yd mod n,这里x,y∈Zn;
(6)p,q销毁,以{e,n}为公开密钥,{d,n}为私有密钥。
实例:
1. 假设p = 3、q = 11(p,q都是素数即可。),则N = pq = 33;
2. r =Φ(n)= (p-1)(q-1) = (3-1)(11-1) = 20;
3. 根据gcd(e,Φ(n))=1,即gcd(e,20)=1,令e=3,则,d = 7。(两个数交换一下也可以。)
到这里,公钥和密钥已经确定。公钥为(N, e) = (33, 3),密钥为(N, d) = (33, 7)。
代码实现:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
|
public class SimpleRSA
{ /** *
加密、解密算法 *
@param key 公钥或密钥 *
@param message 数据 *
@return */ public static long rsa(int baseNum, int key, long message){ if(baseNum
< 1 ||
key < 1){ return 0L; } //加密或者解密之后的数据 long rsaMessage
= 0L; //加密核心算法 rsaMessage
= Math.round(Math.pow(message, key)) % baseNum; return rsaMessage; } public static void main(String[]
args){ //基数 int baseNum
= 3 * 11; //公钥 int keyE
= 3; //密钥 int keyD
= 7; //未加密的数据 long msg
= 24L; //加密后的数据 long encodeMsg
= rsa(baseNum, keyE, msg); //解密后的数据 long decodeMsg
= rsa(baseNum, keyD, encodeMsg); System.out.println("加密前:" +
msg); System.out.println("加密后:" +
encodeMsg); System.out.println("解密后:" +
decodeMsg); }} |
结果:这样CA就保存了用户的公钥,其他任何人想法送给此用户信息,只需查询词公钥,加密发送即可,而此用户用只有自己知道的秘钥解密。
3、签名证书:
签名证书的用途:加入有A用户向B用户发送了信息“A love you”,B接收到之后怎么确定就是A发送的呢(因为中间人攻击中,假如C截获了A发送的信息后,改成“C love you”,B是无法确定这两个信息的发送者,因他她们都同样用B的工要加密),于是产生了签名证书技术。
签名证书是由CA用自己的私钥对用户的信息进行加密,并把发给用户的,用户可以在发送信息的过程中附加上自己的签名证书,让接受者验证信息的来源。当接受者接受到发送者的签名证书后即可用ca的公钥解密验证发送者的身份信息。
4、信息传输:
过程:
A. Alice 准备好要传送的数字信息(明文)。
B. Alice 对数字信息进行哈希(hash)运算,得到一个信息摘要。
C. Alice 用自己的私钥(SK)对信息摘要进行加密得到Alice 的数字签名,并将其附在数字信息上。
D. Alice 用Bob 的公钥(PK)对刚才随机产生的加密密钥进行加密,将加密后的密文传送给Bob
E. Bob 收到Alice 传送过来的密文,用自己的私钥(SK)对密文解密。
F. Bob 用Alice 的公钥(PK)对Alice 的数字签名进行解密,得到信息摘要。
G. Bob 用相同的hash 算法对收到的明文再进行一次hash 运算,得到一个新的信息摘要。
H. Bob 将收到的信息摘要和新产生的信息摘要进行比较,如果一致,说明收到的信息没有被修改过。
采用数字签名,能完成这些功能:
(1)确认信息是由签名者发送的;
(2)确认信息自签名后到收到为止,未被修改过;
(3)签名者无法否认信息是由自己发送的。
但是上述过程存在问题,例如有用户C窃取A的电脑信息,把B的公钥修改成了自己的公钥,A用此公钥加密信息发给B,C在中间截获这个数据就可以获取这些私密信息。怎么应对这种情况呢?签名证书就派上用场了。
证书中心用自己的私钥,对每一个用户的、的公钥和一些相关信息一起加密,生成"数字证书"(Digital Certificate)。发送者在发送信息之前如果想核对接受者的公钥,只需用CA的公钥对B的签名证书进行解密确认即可。