一:二叉树的前序遍历、中序遍历和后续遍历
二叉树的遍历口决
前序遍历:根节点----左子树----右子树
中序遍历:左子树----根节点----右子树
后序遍历:左子树----右子树----根节点
note:
1.在二叉树中,遍历都是从左到右的。在上面的前序、中序和后序遍历中,永远都是左子树排在右子树前面
2.在二叉树的前序遍历、中序遍历、后续遍历中,前、中、后指的是根节点的顺序。前序就是根节点在前,中序就是根节点在中,后续就是根节点在后。
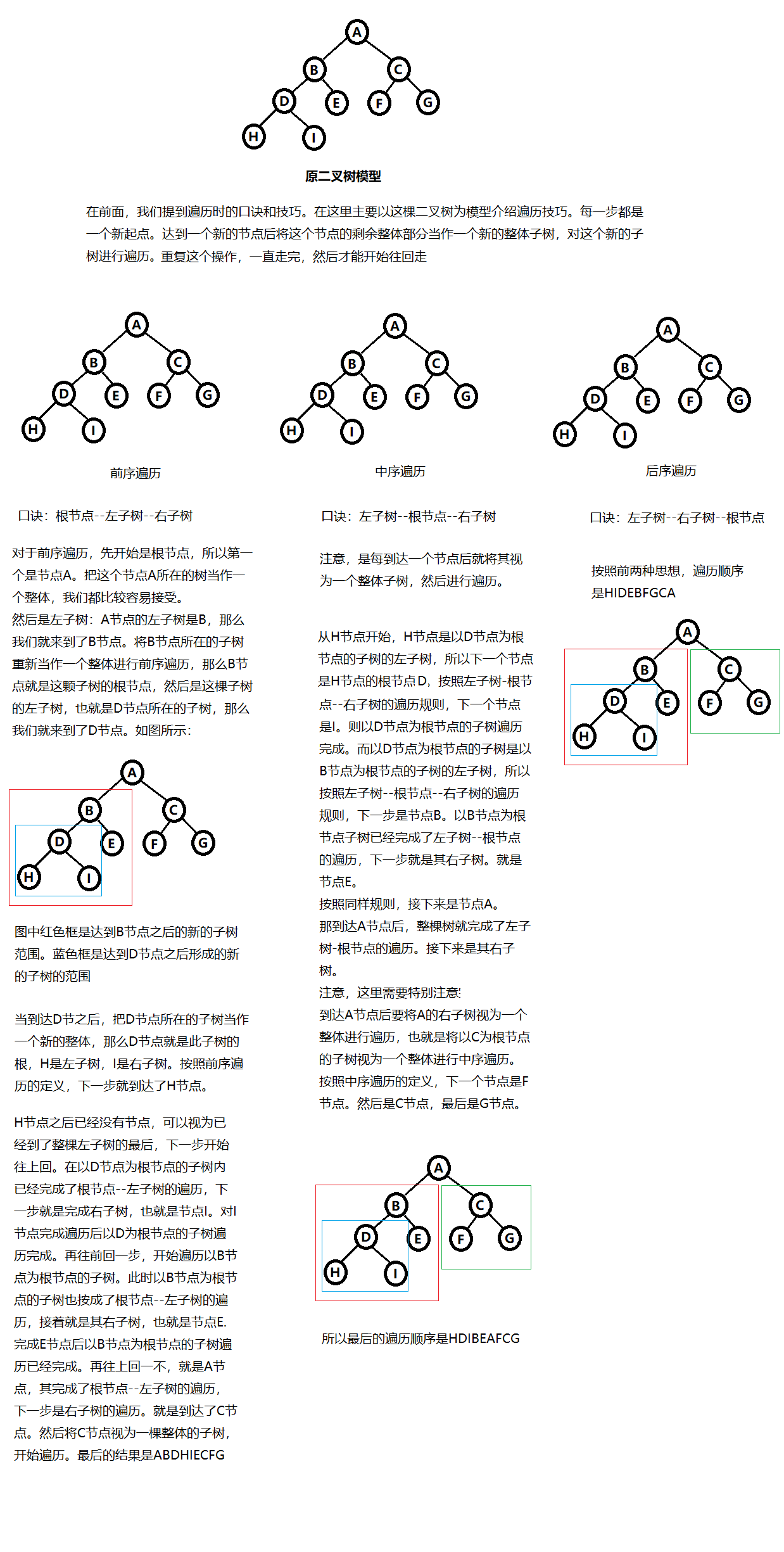
知道了前序、中序和后序遍历的口诀后,介绍一下在遍历过程中的技巧。并且在后面会以图的形式说明。
技巧:每一步都是一个新起点。我们在遍历的时候,每到达一个节点,就将其当作新起点,并且把这个节点所在子树部分当作一个新的整体。在这个新的整体上继续实施遍历算法,一直执行到最后,然后再返回继续。这个就是递归,在二叉树的前序遍历,中序遍历和后序遍历的算法实现时就是采用的遍历手段来实现的。
示意图如下
二、二叉树的链式存储
引言:所有的数据结构都有四种存储方式:顺序存储、链式存储、索引存储和散列存储方法。在这里只介绍二叉树的链式存储。
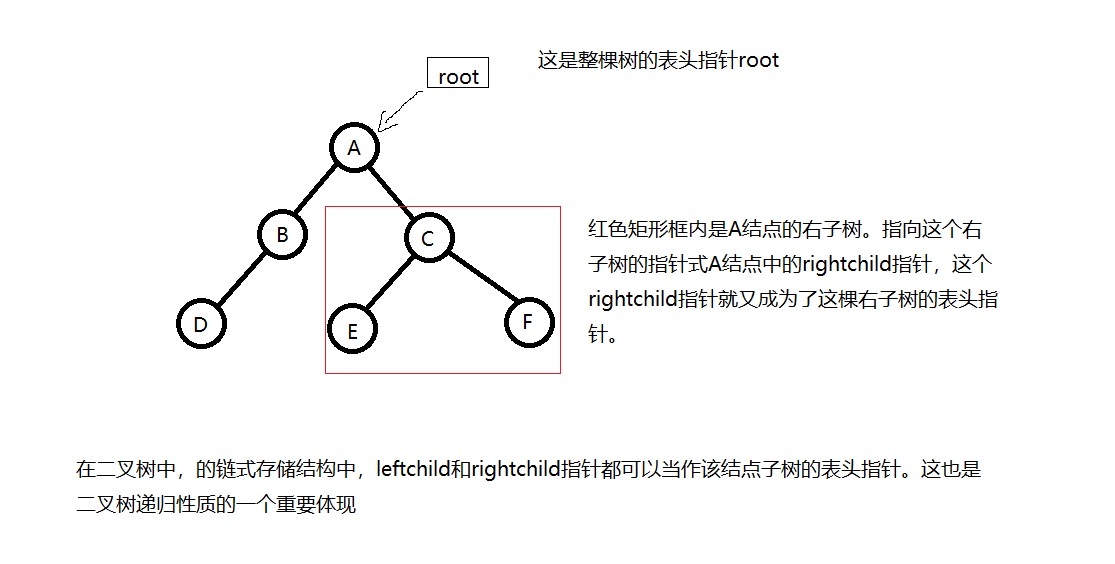
在二叉树的链式存储中,每个节点都是用一个结构体或者类来表示。根据二叉树的定义,二叉树的每一个节点可以有两个分支,分别指向结点的左子树和右子树。因此,每个节点至少包含三个域,分别存放节点数据的数据域data、存放左子女节点指针的leftchild和存放右子女结点指针的rightchild。二叉树的这种链式存储结构称为二叉链表。使用二叉链表,可以很方便的根据结点leftchild指针和rightchild指针找到他的左子女和右子女。但是想要找到双亲节点却很困难。为了便于查找任一节点的双亲结点,可以在结点中再增加一个只想双亲的指针域parent,此时链表被成为三叉链表。

与线性表的链式存储一样,在二叉树的存储中同样有一个表头指针。有了这个表头指针,我们就根据结点中指向其子女的指针来查找和操作整棵树中的所有结点。所以对建立好的二叉树操作时,传入这个表头指针即可。在完成建立二叉树的操作后,只要返回这个表头指针就相当于存储了整棵二叉树。
由于二叉树在定义的时候是采用递归的方式来定义的,所以二叉树本身就是一个可以递归的数据结构。
我们知道,二叉树是采用递归来定义的,并且二叉树本身就是递归性质的数据结构。所以在二叉树的查找,建立,删除和遍历等操作的算法中都是通过递归操作来实现的。
在构造二叉树的时候先进行基础零部件的构建,对于二叉树来说,就是结点的建立。构造二叉树结点程序。
/** 使用二叉链表来存储二叉树 建立二叉链表的泛型编程 */ template<class T> struct BinTreeNode{ //结点的数据域,可以根据实际需要增加或减少数据域 T data; //定义结点中指向该结点左右子女的指针域 BinTreeNode<T>* leftchild; BinTreeNode<T>* rightchild; //使用列表初始化对leftchild和rightchild进行初始化 //这个是默认构造函数 //因为每一种基础数据类型的data,在声明时都会提供默认初始化,所以并没有对data进行初始化 BinTreeNode():leftchild(NULL),rightchild(NULL){} //建立结点时使用列表初始化进行结点的建立 BinTreeNode(T x, BinTreeNode<T>* left = NULL, BinTreeNode<T>* right = NULL):data(x), leftchild(left), rightchild(right) }