B树的结构有:B-Tree, B-Tree, B*Tree
BTree(二叉排序树)B-Tree:B树也是二叉排序树的变异版本,是N叉的排序树。
M阶BTree的几个重要特性
1.结点最多含m棵子树(指针),m-1个关键字(存的数据,空间)(m >= 2)
2.除根节点和叶子结点外,其它每个结点至少有ceil(m / 2)个子节点,ceil向上取整
3.若根节点不是叶子节点,则至少有两棵子树。
二叉排序树BST,也称二叉查找树
在二叉查找树中,因为中序遍历的顺序是 左子树, 根, 右子树,而在二叉排序树中,左子树结点值 < 根节点值 < 右子树结点值,所以,二叉排序树的中序遍历序列是递增的结果。
二叉排序树的中序遍历序列一定是一个递增的有序序列。
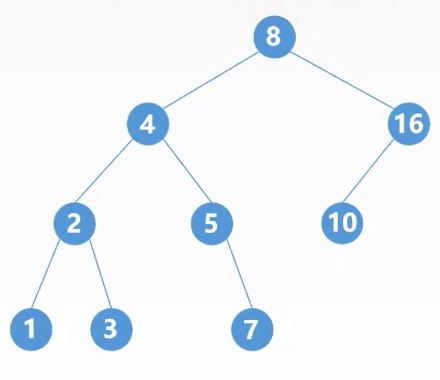
对于这棵树,中序遍历序列是:1, 2, 3, 4, 5, 7, 8, 10, 16
对于二叉排序树而言,我们最常用的操作并不是排序,而是查找。
查找操作
1.判断二叉树是否为空
2.二叉树若不为空,则查找根节点,若相等则查找成功
3.若根节点不相等,则当小于根节点则查找左子树;当大于根结点值时则查找右子树。
4.当查找到叶节点仍没查找到相对应的值(判断指针是否为空),则查找失败。
该算法的时间复杂度为O(h)
1 BSTNode* BST_Search(BiTree T, ElemType key, BSTNode* &p) 2 { 3 p = NULL; 4 while(T != NULL && key != T.data) 5 { 6 if(key < T.data) 7 T = T -> lchild; 8 if(key > T.data) 9 T = T -> rchild; 10 } 11 return T; 12 13 }
插入
若二叉排序树为空,则直接插入结点
若二叉排序树非空,当值小于根节点时插入左子树;当值大于根节点时,插入右子树,当值等于根节点时不进行插入。
注意,在树的实现中,我们是通过二叉链表或者三叉链表来实现的,所以我们在插入操作或者删除操作时修改指针指向即可。
1 //返回的是整型变量,若插入成功则返回值1,插入失败则返回值0 2 int BST_Insert(BiTree &T, KeyType k){ 3 if(T == NULL) 4 { 5 T = (BiTree)malloc(sizeof(BSTNode)); 6 T->data = k; 7 T -> lchild = NULL; 8 T -> rchild = NULL; 9 return1; 10 } 11 12 else if(key == T->data) 13 return 0; 14 15 else if(key > T -> data) 16 return BST_Insert(T->rchild, k); 17 18 else 19 return BST_Insert(T->lchild, k) 20 21 }
构造二叉排序树
构造二叉排序树是一个动态的问题。就是不断调用插入函数进行构造二叉排序树。
读入一个元素并建立结点,若二叉树为空,则将其作为根节点;
若二叉树非空,当值小于根结点时,插入左子树;当值大于根节点时,插入右子树;当值等于根节点时不进行插入。
1 void Create_BST(BiTree &T, KeyType str[], int n){ 2 T = NULL; 3 int i = 0; 4 while(i < n) 5 { 6 BST_Insert(T, str[i]); 7 i++; 8 } 9 }
但是这样的构造法生成的二叉顺序树与元素的顺序有关
删除操作
二叉排序树的删除操作是比较复杂的,分为以下三种情况
1.所被删除的结点是叶节点,则直接删除
2.若被删除的结点只有一棵子树,则让该结点的子树称为该节点父结点的子树,从而代替该节点
3.若被删除的结点右两棵子树,则让该节点的中序序列直接后继代替该节点,并删除直接后继结点。
这里只做第三种情况的分析。
第三种情况中,被删除的中序直接后继节点是比该结点值大,但是又是比被删除结点的右子树中其他结点值小的一个结点,所以将被删除结点的中序直接后继结点代替该结点时最合适的操作。

在删除二叉排序树中删除并插入某结点,得到的二叉排序树是否与原来相同。
答案是可能相同,也可能不同,要视情况具体分析。
仍以上图中图1所示的二叉排序树为例,若删除的是结点7,那么得到的二叉排序树是相同的。
但是若删除的是结点5,那么再重新将该节点插入该二叉树时,结点5就会成为结点7的左孩子结点。
二叉排序树的查找效率
平均查找长度(ASL)取决于树的高度。
如果二叉排序树是平衡二叉树的话,查找效率是O(log2n), 最坏情况下是O(n),此时二叉排序树类似于单链表。
平衡二叉树
平衡二叉树AVL:任意结点的平衡因子的绝对值不超过1。
平衡因子:左子树高度与右子树高度之差
高度为h的最小平衡二叉树的结点数Nh的计算
Nh = Nh-1 + Nh-2 + 1
N0 = 0
N1 = 1
平衡二叉树的后序遍历过程
利用递归的后序遍历过程:
1.判断左子树是一棵平衡二叉树
2.判断右子树是一棵平衡二叉树
3.判断以该节点为根的二叉树为平衡二叉树
判断条件:若左子树和右子树均为平衡二叉树,且左子树与右子树高度差的绝对值小于等于1,则平衡。
需要保留两个变量:表示平衡性的变量B,为布尔类型,平衡为1,不平衡为0;表示高度的变量,为整型。

1 void Judge_AVL(BiTree bt, int &balance, int &h) 2 { 3 //左子树的平衡性、右子树的平衡性, 左子树的高度,右子树的高度 4 int bl = 0; br = 0, hl = 0; hr = 0; 5 if(bt == NULL) 6 { 7 h = 0; 8 balance = 1; 9 } 10 11 else if(bt -> lchild == NULL && bt -> rchild == NULL) 12 { 13 h = 1; 14 balance = 1; 15 } 16 17 else 18 { 19 Judge_AVL(bt->lchild, bl, hl); 20 Judge_AVL(bt -> rchild, br, hr); 21 if(hl > hr) 22 h = hr + 1; 23 else 24 h = hl + 1; 25 26 27 if(abs(hl - hr) < 2 && bl ==1 && br == 1) 28 balance = 1; 29 else 30 balance = 0; 31 } 32 }
插入操作
先按照二叉排序树的插入过程进行插入,然后对插入后的二叉排序树进行调整,将其调整为平衡二叉树。
调整过程:调整过程是针对最小的不平衡子树,也就是从我们的插入结点开始依次向上找到最小的不平衡子树。
根据不平衡的情况,我们分为了四种调整的过程。
LL平衡旋转(右单旋转)
原因:在结点A的左孩子的左子树上插入新结点导致二叉树的不平衡
调整方法:右旋操作:将A的左孩子B代替A,将A结点称为B的右子树根节点,而B的原右子树作为A的左子树。
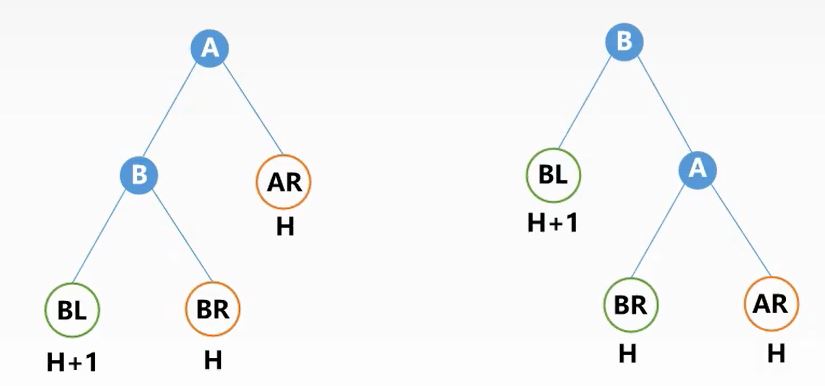
RR平衡旋转(左单旋转)
原因:在结点A的右孩子的右子树上插入了新结点导致了二叉树的不平衡
调整:左旋操作,将A的右孩子B代替A,将A结点称为B的左子树根结点,而B的原左子数则作为A的右子树。

LR平衡旋转(先左后右双旋转)
原因:在结点A的左孩子的右子树上插入了新结点
调整:先左旋后右旋操作:先将A的左孩子B的右孩子结点C代替B,然后再将C结点向上代替A的位置
1.在本图中,既可以插到C结点的左子树CL上,也可以插到C结点的右子树CR上
2.本图是将结点插入到了CL子树上,所以CL是H层, CR是H-1层。
3.之所以标注(H)是考虑到CL和CR可能是空的

RL平衡旋转(先右后做双旋转)
原因:在结点A的右孩子的左子树上插入了新结点
调整方法:先右旋后左旋操作:将A的右孩子B的左孩子结点C代替B,然后再将C结点向上代替A的位置
