一.概念
基数排序也不是基于比较和元素移位的,又称桶子法;数据结构课本上首先由扑克牌的排序引入,继而引出多关键字比较。
本文是基于计数排序的基数排序,只介绍最低位优先(Least Significant Digit First),谷歌之发现就几乎没有介绍MSD的,所谓LSD就是从数字的最低位逐个比较,比较的趟数就是最大数字的位数digit,因此需要先用countDigit方法求出位数digit。
局限性:本算法是稳定的,LSD需要使用稳定的算法,由于按位比较,因此需要整数,和计数排序不同的是,整数可以是负数(各种排序都可以正负混合),也可以很大,为什么呢?
- 数值较大:由于是按比较,统计数字出现次数时只需要开c[10]就好, 因为就0到9共10个数字。
- 负数:若是有正有负怎么办呢?这个是写的时候想起来的,不过我立马想到了解决办法,请各位看官想想,看和我的是否一样:把正负数分开存入两个数组,负数数组先去掉负号按正数进行由大到小的基数排序,输出的时候加上负号正序输出;正数数组就直接由小到大排序,然后正序输出,不知各位看管和我想的是否一致。
- 求位数:digit = (int)Math.ceil(Math.log10(max))或者String s = max +""; digit = s.length()。
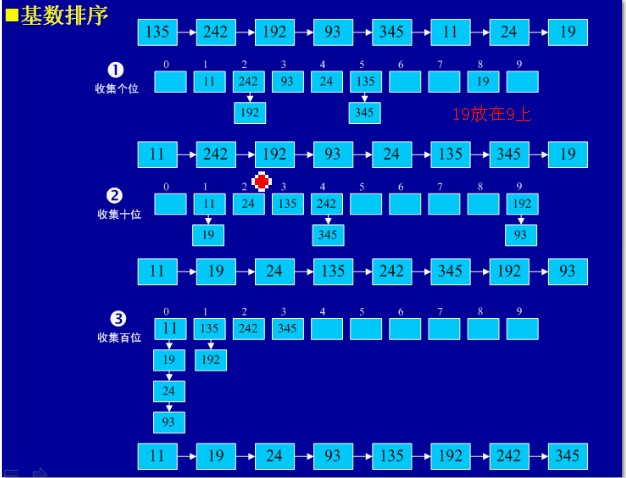
二.算法描述
有的读者会问为什么LSD需要稳定的排序方法呢?下面就笔者的一点见解略作探讨……我刚开始也迷惑,迷惑的原因在于原来计数排序是直接比较数值不是每一位数字,现在比较每位数字,这样就把每个数拆分了,若是不稳定排序,则可能下一次排序就把上一次的打乱了。再来说下稳定,有同学问如果每个数都不相同是否就不涉及稳定的问题呢?明白上面分析的读者会立刻回答否,因为是按数字比较的,而数字只有0到9,肯定有相同的。
如上图,经过个位比较后345必定在242后边(因为5>2),实际也确实应该这样,由于二者的十位数字都是4,如果十位排序是不稳定排序,则很可能下一次345就排在242前边了,很明显就错了。
三.算法Java实现
import java.util.Arrays; public class RadixSort { //基于计数排序的基数排序算法 public static void radixSort(int[] array,int radix, int digit) { //array为待排序数组 //radix,代表基数,实际就是几个数字,那就是10喽 //digit代表排序元素的位数,实际意义是排序趟数 int length = array.length; int[] res = new int[length]; int[] c = new int[radix];//radix就是10,因为0到9共10个数字 int divide = 1;//用于每次把数字缩小10倍 for (int i = 0; i < digit; i++) { res = Arrays.copyOf(array, length); Arrays.fill(c, 0); for (int j = 0; j < length; j++) { int tempKey = (res[j]/divide)%radix; c[tempKey]++; } for (int j = 1; j < radix; j++) { c [j] = c[j] + c[j-1]; } for (int j=length-1; j>=0; j--) { int tempKey = (res[j]/divide)%radix; array[c[tempKey]-1] = res[j]; c[tempKey]--; } divide = divide * radix; } } public static int countDigit(int[] array) { int max = array[0]; for (int i = 1; i < array.length; i++) { if (array[i] > max) { max = array[i]; } } int time = 0; while (max > 0) { max /= 10; time++; } return time; } public static void main(String[] args) { int[] array = {3,2,3,2,5,333,45566,2345678,78,990,12,432,56}; int time = countDigit(array); //System.out.println(time); radixSort(array,10,time); for (int i = 0; i < array.length; i++) { System.out.print(" " + array[i]); } } }