Matlab计算矩阵和函数梯度

一、差分与微分

　　我自己的理解。

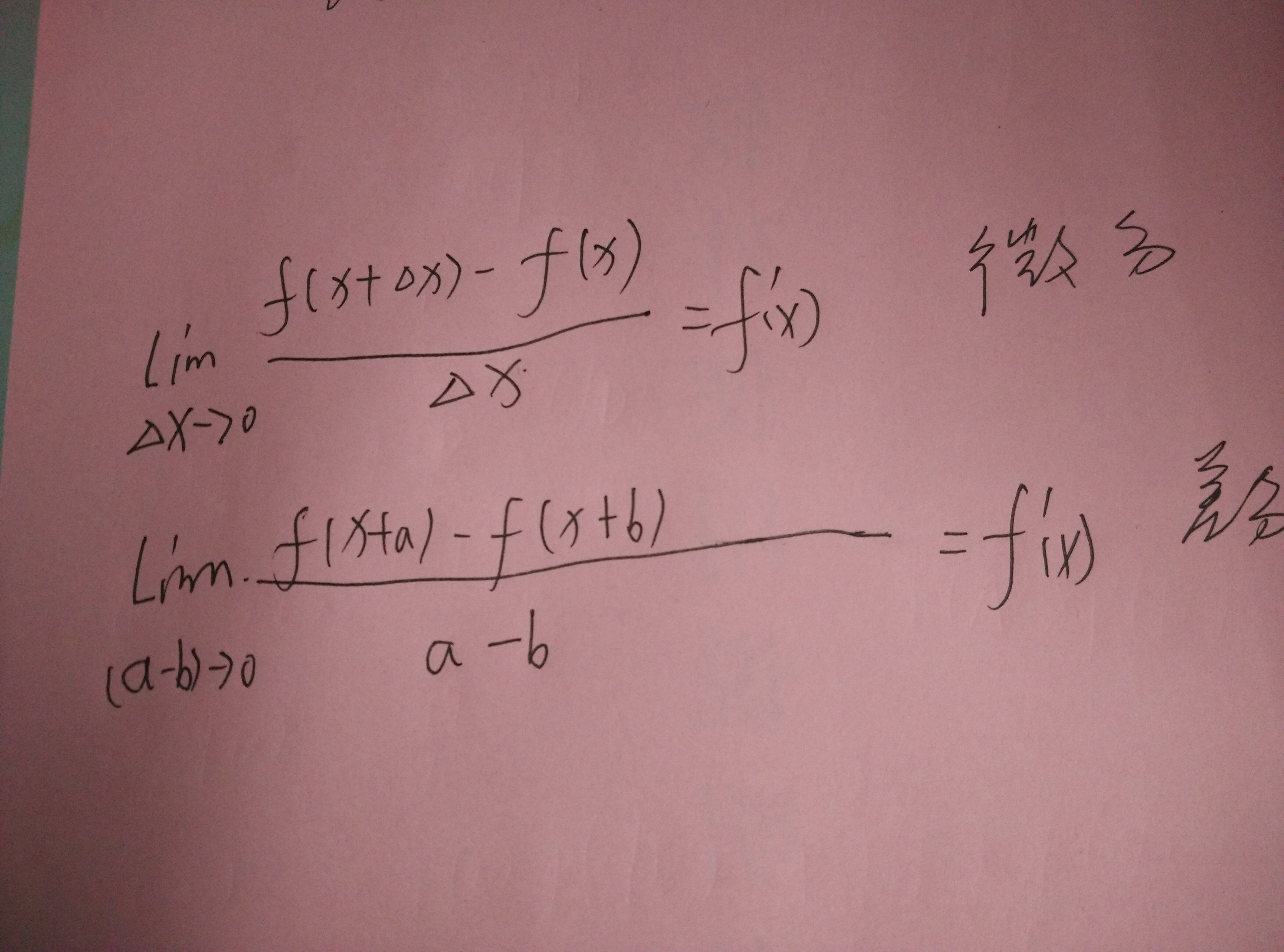
二、求解

　　2.1 矩阵

　　这就是matlab的计算结果.太小的话放大些:

c =
     4     5     9
     7     2     1
     5     2     6
>> [x,y]=gradient(c)
x =
    1.0000    2.5000    4.0000
   -5.0000   -3.0000   -1.0000
   -3.0000    0.5000    4.0000
y =
    3.0000   -3.0000   -8.0000
    0.5000   -1.5000   -1.5000
   -2.0000         0    5.0000

　　先看x,x就是矩阵的横向梯度，怎么求解的呢，第一列就是的数值就是第二列减去第一列的值除以1   比如-5=（2-7）/1.第2列就是第二列减去第一列的值加上第三列减去第二列的值再除以2，比如：-3=（（2-7）+（1-2））/2.最后一列比较特殊，因为它之后没有其余列了，于是最后一列=最后一列减去倒数第二列除以1.比如-1=（1-2）/1.y的求解跟1就是一个性质了  。

　　2.2 二元函数

　　在上MATLAB课的时候,有学生问怎么用gradient函数求f=2x²+3y³的梯度啊,不懂得怎么写格式,试了很多次都不行.解答如下:
　　在MATALB中,求梯度只能是求数值梯度,所以必须将函数f离散化,用差分代替微分,精度取决于差分步长,因为现在计算机速度足够快,所以差分可以取得足够小,也不影响计算速度和计算精度.方法如下:

 X=-6:0.6:6;   %计算区间是[-6 6],步长0.6
Y=X; 
[x,y]=meshgrid(X,Y)    %生成计算网格
f=2.*x.^2+3.*y.^3      %计算网格结点上的函数值
[Dx,Dy]=gradient(f)    %用数值方法求函数梯度
quiver(X,Y,Dx,Dy)    %用矢量绘图函数绘出梯度矢量大小分布
hold on 
contour(X,Y,f)    %与梯度值对应,绘出原函数的等值线图