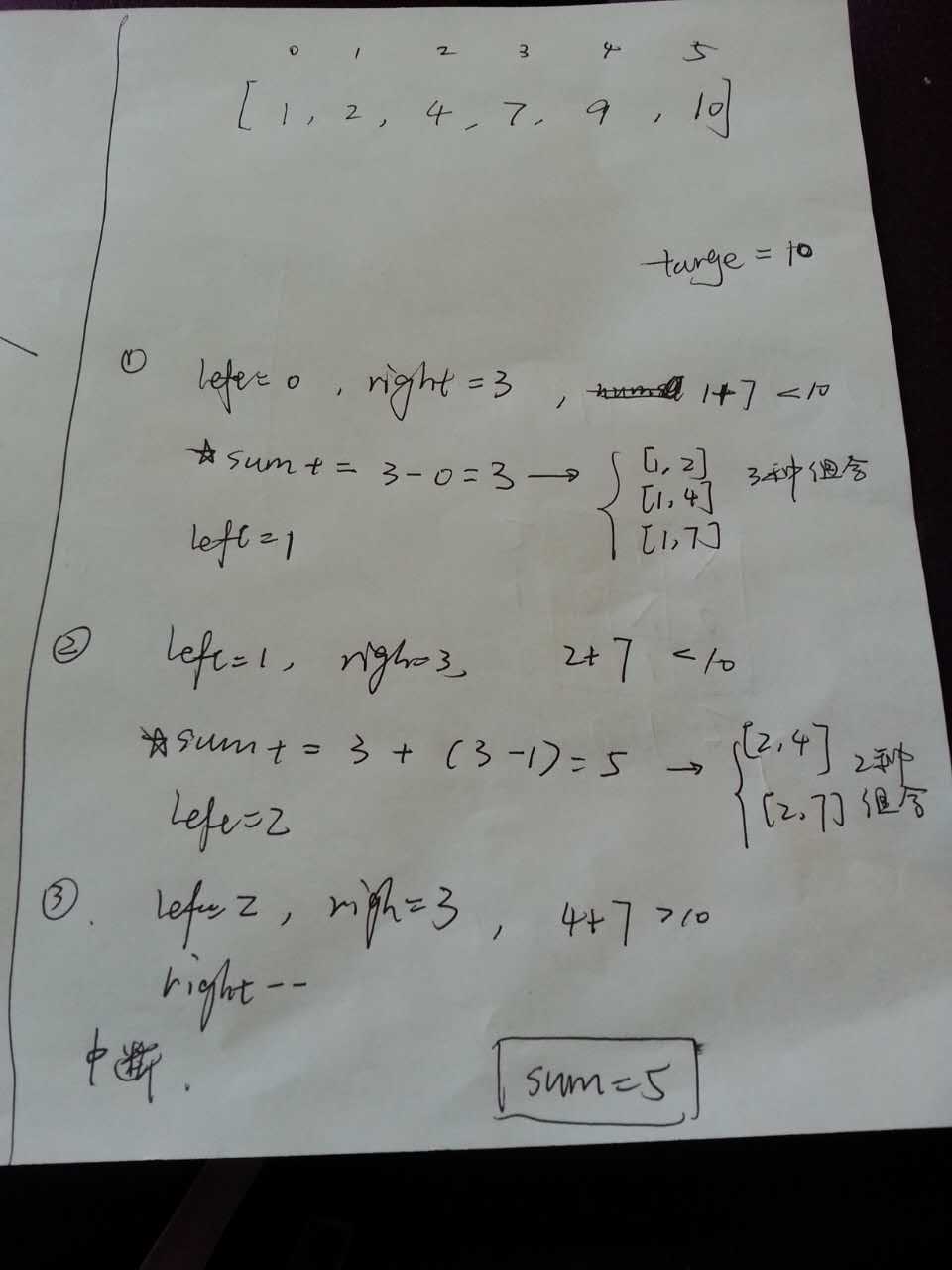Given an array of n integers nums and a target, find the number of index triplets i, j, k with 0 <= i < j < k < n that satisfy the condition nums[i] + nums[j] + nums[k] < target.
For example, given nums = [-2, 0, 1, 3], and target = 2.
Return 2. Because there are two triplets which sums are less than 2:
[-2, 0, 1] [-2, 0, 3]
Follow up:
Could you solve it in O(n2) runtime?
public class Solution { public int threeSumSmaller(int[] nums, int target) { Arrays.sort(nums); int sum = 0; for (int i = 0; i < nums.length - 2; i++) { sum += twoSumSmaller(nums, i + 1, target - nums[i]); } return sum; } private int twoSumSmaller(int[] nums, int startIndex, int target) { int sum = 0; int left = startIndex; int right = nums.length - 1; while (left < right) { if (nums[left] + nums[right] < target) { sum += right - left; left++; } else { right--; } } return sum; } }