图的割边

2019-10-05 23:40:13

一、定义

割点：去掉一个顶点及其相邻的边，图的连通分量增加。

割边：去掉一条边，图的连通分量增加。

两者关系

• 有割点不一定有割边，有割边一定存在割点
• 割边一定是割点依附的边

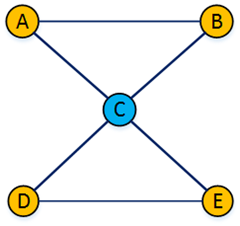
如下图，点C是割点，但是图中不存在割边。

二、Tarjan算法

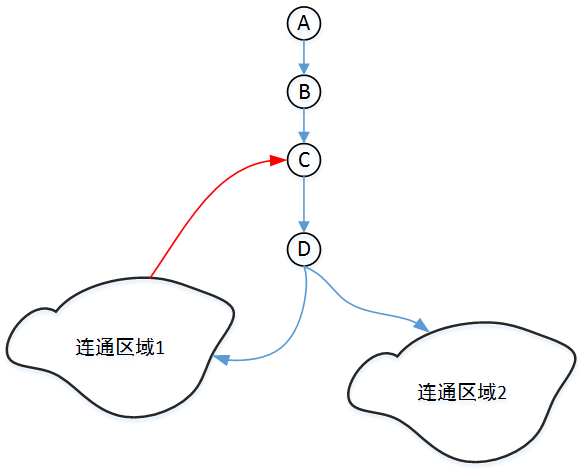
使用Tarjan算法可以在一次dfs里得到所有的割边。

• 为所有节点按照dfs遍历顺序打上时间戳
• 为所有节点记录非父节点能到达的最小的时间戳（包括自己）
• 如果一个节点不通过父节点可以通向比父节点时间戳更小的节点，那么父节点必不是割点
• 如果一个节点的子节点能到达的最小的时间戳比自己小，那么这两点可以构成割边

三、例题 

• Critical Connections in a Network

问题描述：

 

问题求解：

Tarjan算法，可以在O(n + e)的时间复杂度求解。

    int time = 0;
    
    public List<List<Integer>> criticalConnections(int n, List<List<Integer>> connections) {
        List<List<Integer>> res = new ArrayList<>();
        int[] ts = new int[n];
        int[] lo = new int[n];
        List<Integer>[] graph = new List[n];
        Arrays.fill(ts, -1);
        for (int i = 0; i < n; i++) graph[i] = new ArrayList<>();
        for (List<Integer> con : connections) {
            graph[con.get(0)].add(con.get(1));
            graph[con.get(1)].add(con.get(0));
        }
        dfs(graph, 0, -1, ts, lo, res);
        return res;
    }
    
    private void dfs(List<Integer>[] graph, int node, int prev, int[] ts, int[] lo, List<List<Integer>> res) {
        ts[node] = time;
        lo[node] = time;
        time = time + 1;
        for (int next : graph[node]) {
            if (next == prev) continue;
            if (ts[next] == -1) {
                dfs(graph, next, node, ts, lo, res);
                if (lo[next] > ts[node]) res.add(Arrays.asList(node, next));
            }
            lo[node] = Math.min(lo[node], lo[next]);
        }
    }