2018-09-27 23:33:49
问题描述:
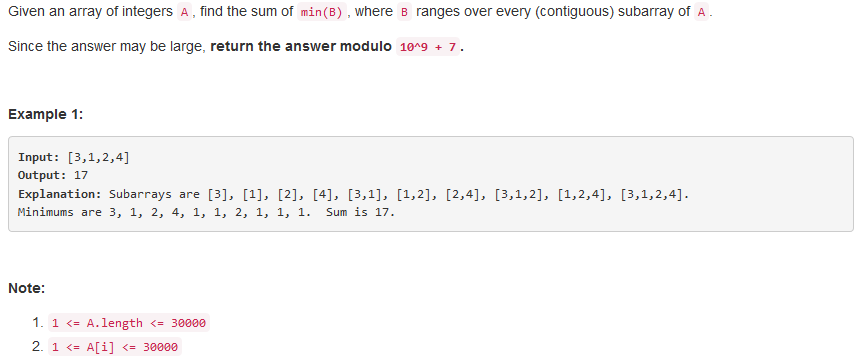
问题求解:
方法一、DP(MLE)
动态规划的想法应该是比较容易想到的解法了,因为非常的直观,但是本题的数据规模还是比较大的,如果直接使用动态规划,即使不MLE,也是肯定会在大规模的数据量上TLE的。
public int sumSubarrayMins(int[] A) {
int res = 0;
int mod = (int)Math.pow(10, 9) + 7;
int[][] dp = new int[A.length][A.length];
for (int i = 0; i < A.length; i++) dp[i][i] = A[i];
for (int len = 2; len <= A.length; len++) {
for (int i = 0; i <= A.length - len; i++) {
int j = i + len - 1;
dp[i][j] = Math.min(dp[i + 1][j], dp[i][j - 1]);
}
}
for (int i = 0; i < A.length; i++) {
for (int j = 0; j < A.length; j++) {
res = (res + dp[i][j]) % mod;
}
}
return res;
}
方法二、
数据量已经基本表明时间复杂度在O(nlogn)左右比较好,那么直接使用dp肯定是不会通过所有的例子的。
本题还有另外一种思路:
res = sum(A[i] * f(i))
wheref(i)is the number of subarrays,
in whichA[i]is the minimum.
难点就在于求f(i),为了求f(i)需要求left[i]和right[i]。
left[i]:A[i]左边严格大于A[i]的个数
right[i]:A[i]右边大于等于A[i]的个数
f(i) = (left[i] + 1) * (right[i] + 1),其实就是一个排列组合,左边取一个可能,那么可以从右边取right[i] + 1种来进行组合。
这里需要特别注意的一点是:首先本问题是允许重复的子数组的,这里的重复是指数字上相等,但是是不允许完全一致的区间,因此左边必须是严格大于,否则会出现重复的情况。计算left,right数组可以使用Stack在O(n)时间复杂度完成求解,最后的res计算也是线性时间,因此总的时间复杂度为O(n)。
public int sumSubarrayMins(int[] A) {
int res = 0;
int mod = (int)1e9 + 7;
int[] left = new int[A.length];
int[] right = new int[A.length];
Stack<int[]> stack = new Stack<>();
stack.push(new int[]{Integer.MIN_VALUE, -1});
for (int i = 0; i < A.length; i++) {
while (stack.peek()[0] > A[i])
stack.pop();
left[i] = i - stack.peek()[1];
stack.push(new int[]{A[i], i});
}
stack.clear();
stack.push(new int[]{Integer.MIN_VALUE, A.length});
for (int i = A.length - 1; i >= 0; i--) {
while (stack.peek()[0] >= A[i])
stack.pop();
right[i] = stack.peek()[1] - i;
stack.push(new int[]{A[i], i});
}
for (int i = 0; i < A.length; i++) {
res = (res + A[i] * left[i] * right[i]) % mod;
}
return res;
}