Kaggle竞赛实战系列（一）：手写数字识别器（Digit Recognizer）得分99.53％、99.91%和100%

欢迎关注WX公众号：【程序员管小亮】

专栏——Kaggle竞赛实战系列

文章目录

• 欢迎关注WX公众号：【程序员管小亮】
• 专栏——Kaggle竞赛实战系列
• 一、介绍
• 二、数据准备
• 2.1、数据加载
• 2.2、数据可视化
• 2.3、数据清洗
• 2.4、归一化
• 2.5、Reshape
• 2.6、标签编码
• 2.7、分割交叉验证集
• 三、卷积神经网络CNN
• 3.1、定义网络模型
• 3.2、设置优化器和退火函数
• 3.3、数据增强
• 3.4、拟合数据
• 四、评估模型
• 4.1、训练和验证曲线
• 4.2、混淆矩阵
• 4.3、预测和提交
• 五、MNIST上的最佳模型
• 六、不应该被提交的结果
• 七、MNIST上的最佳CNN
• 八、初代网络 LeNet-5
• 九、GitHub
• 参考文章

一、介绍

• 个人 Kaggle 地址：https://www.kaggle.com/tefuirnever

• GitHub 代码地址：https://github.com/TeFuirnever/Kaggle-Digit-Recognizer

• 【Digit Recognizer】比赛页面：https://www.kaggle.com/c/digit-recognizer/overview
  

MNIST 是计算机视觉领域的 hello world 数据集。自从1999年发布以来，这个经典的手写数字识别数据集就成为分类算法的基础，即使新的机器学习技术在不停地出现，但 MNIST 仍然是研究人员和学习者的可靠资源。

这里选择用 keras API（Tensorflow backend）来构建它，这会使得整个过程非常直观且便于理解，具体过程如下：

导入需要的库。

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
import seaborn as sns
%matplotlib inline

np.random.seed(2)

from sklearn.model_selection import train_test_split
from sklearn.metrics import confusion_matrix
import itertools

# 转换为独热编码
from keras.utils.np_utils import to_categorical
from keras.models import Sequential
from keras.layers import Dense, Dropout, Flatten, Conv2D, MaxPool2D, BatchNormalization
from keras.optimizers import RMSprop
from keras.preprocessing.image import ImageDataGenerator
from keras.callbacks import ReduceLROnPlateau

# 设置显示样式的参数
# http://seaborn.pydata.org/generated/seaborn.set.html
sns.set(style='white', context='notebook', palette='deep')

如果你强迫症犯了的话，使用如下代码可以去除 warning，详细的看这个博客——warnings.filterwarnings(“ignore”)代码解析。

import warnings
warnings.filterwarnings('ignore')

二、数据准备

2.1、数据加载

首先，准备我们所需要的数据（手写数字识别图像）；

# 加载数据
train = pd.read_csv("./train.csv")
test = pd.read_csv("./test.csv")

数据文件 train.csv 和 test.csv 包含从零到九的手绘数字的灰度图像。每个图像的高度为 28 像素，宽度为 28 像素，总计 28 * 28 = 784 像素。

每个像素都有一个与之关联的像素值来表示该像素的明暗程度，此像素值是介于0和255之间的整数（包括0和255），数字越高表示像素越暗。

训练集

以训练数据集（train.csv）为例，共有785列，第一列称为 label，是用户绘制的数字；其余列包含关联图像的像素值。

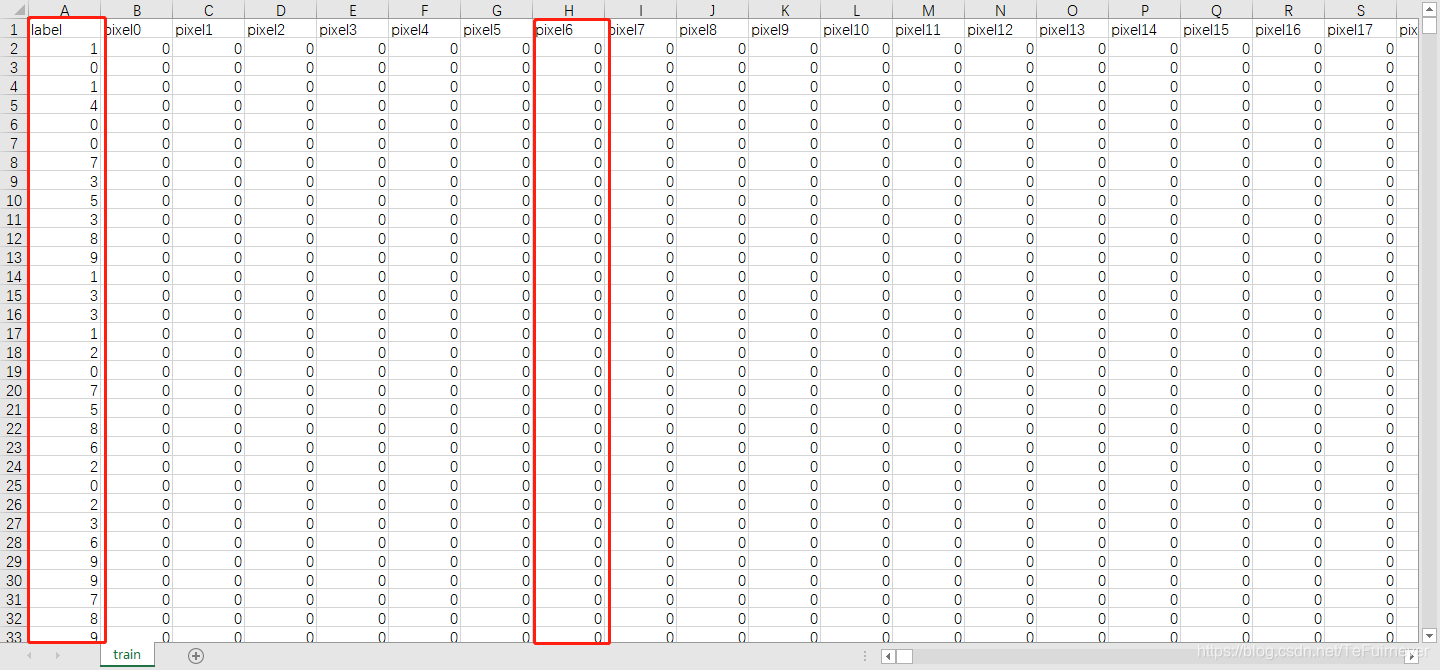
训练集中的每个像素列都有一个类似 pixel x 的名称，其中 x 是0到783之间的整数（包括0和783）。为了在图像上定位这个像素，假设分解了 x 作为 x=i*28+j，其中 i 和 j 是0到27之间的整数（包括0和27），然后 Pixel x 位于 28×28 矩阵的行 i和列 j 上（索引为从零开始的）。例如，pixel 31 表示左起第四列中的像素，以及顶部的第二行，如下图所示：

从视觉上看，如果省略了 pixel 前缀，那么这些像素就构成了这样的图像（即 (2 - 1) * 28 + (4 - 1) = 31）。

测试机

测试数据集（test.csv）与训练集相同，只是它不包含 label 列。

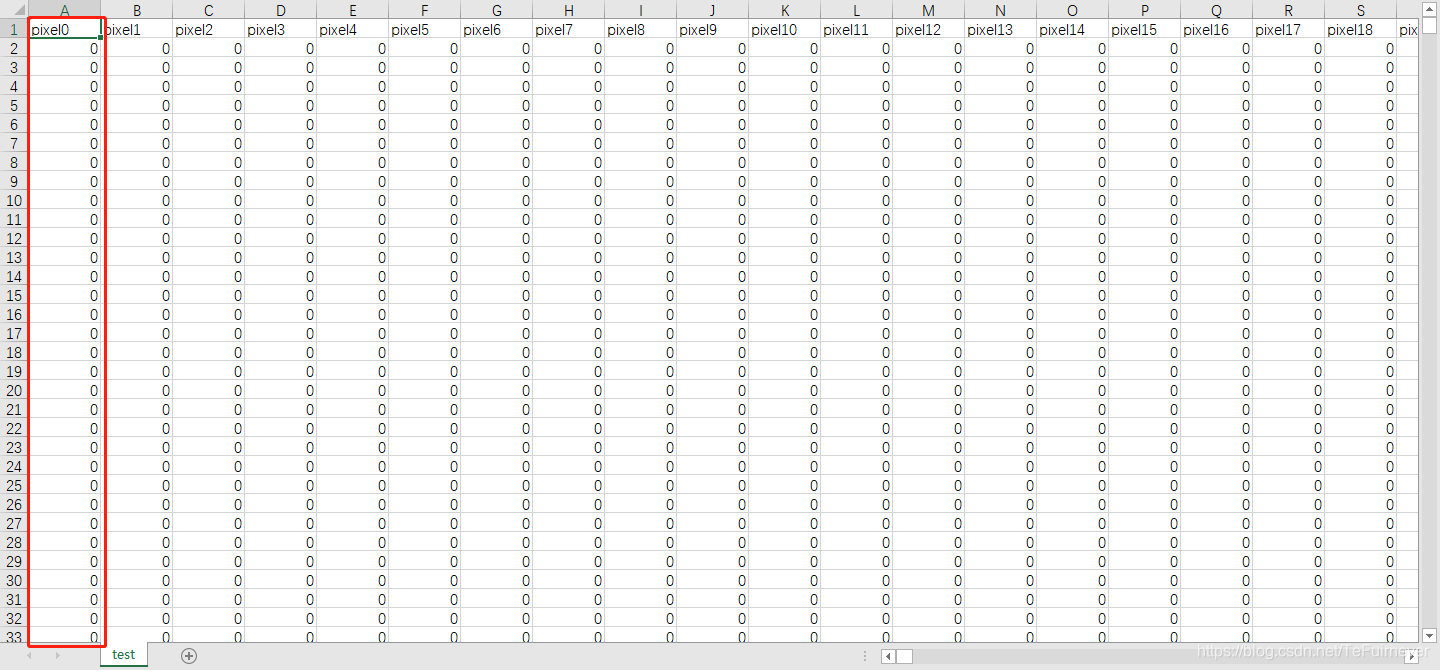
提交文件

提交文件应采用以下格式：对于测试集中28000个图像中的每一个，输出包含 imageid 和预测数字的单行。

例如，如果预测第一个图像为3，第二个图像为7，第三个图像为8，则提交文件将如下所示：

指标

评价标准是 分类准确率，即正确分类的测试图像的比例。例如，分类精度为0.97表示已正确分类了除3%以外的所有图像。

2.2、数据可视化

# 'label'
Y_train = train["label"]
print(Y_train.shape)

# 删除 'label' 列
X_train = train.drop(labels = ["label"],axis = 1) 
print(X_train.shape)

# 释放一些空间
del train

# 使用条形图显示每个分类数据集合中的观测值
# https://seaborn.pydata.org/generated/seaborn.countplot.html?highlight=countplot
g = sns.countplot(Y_train)

# 对训练集中的元素计数
# https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.Series.value_counts.html
Y_train.value_counts()

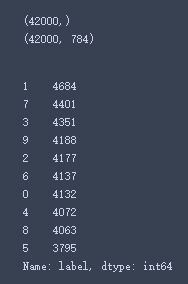
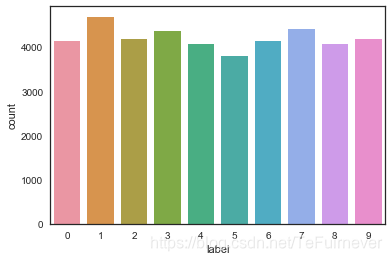
这10位数有类似的计数，都是4000左右。

2.3、数据清洗

# 检查数据
X_train.isnull().any().describe()

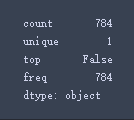
X_train.isnull().any().describe() 将信息进行汇总：

• count 为总统计数；
• unique 为种类（由于该数据中没有空值，全为False，故只有1类）；
• top 为最多的种类；
• freq 为最多的种类出现的频次。

test.isnull().any().describe()

检查是否有损坏的图像（内部缺少值），可以看到训练数据集和测试数据集中没有丢失的值，这样就可以放心地继续处理了。

2.4、归一化

又称标准化/规范化/正则化。

# 对数据进行归一化，到[0, 1]范围内，减小光照的影响，并可加速CNN收敛速度
X_train = X_train / 255.0
test = test / 255.0

2.5、Reshape

# Reshape三维图像(height = 28px, width = 28px , canal = 1)
X_train = X_train.values.reshape(-1,28,28,1)
test = test.values.reshape(-1,28,28,1)

可以看到第一个维度就是数据集中图像的个数；第二和第三个维度是，训练和测试图像（28px * 28px）已作为一个784个值的一维向量储存到 pandas.Dataframe 中；Keras 要求最后一个维度代表通道数，mnist 图像是灰度图，只有一个通道，对于rgb 图像，有3个通道。

2.6、标签编码

# 将标签编码为一个独热向量 (例如: 2 -> [0,0,1,0,0,0,0,0,0,0])
Y_train = to_categorical(Y_train, num_classes = 10)

2.7、分割交叉验证集

# 设置随机种子
random_seed = 2

# 分割出训练集和验证集
X_train, X_val, Y_train, Y_val = train_test_split(X_train, Y_train, test_size = 0.1, random_state=random_seed)

函数参数说明：

print(X_train.shape)

这里选择将训练集分成两部分：一小部分（10%）成为评估模型的验证集，其余（90%）成为评估模型的训练集，用于训练模型。

因为有42000张平衡标签的训练图像，所以随机分割的训练集不会导致一些标签在验证集中被过度表示。如果针对一些不平衡的数据集，一个简单的随机分割可能会导致在验证期间出现不准确的评估。为了避免这种情况，可以在 train_test_split 函数中使用stratify=true 选项（仅适用于 >=0.17sklearn 版本）。

通过可视化图像和查看标签，可以更好地理解其中一个示例。

# 一些例子
g = plt.imshow(X_train[0][:,:,0])

g = plt.imshow(X_train[2][:,:,0])

g = plt.imshow(X_train[2000][:,:,0])

三、卷积神经网络CNN

3.1、定义网络模型

这里使用了 Keras Sequential API，从输入开始，每次只需添加一个层。

• 卷积（conv2d）层就像一组可学习的过滤器：前三个 conv2d 层设置32个过滤器，后三个层设置64个过滤器。

• 池化（maxpool2d）层是一个下采样滤波器：它着眼于2个相邻像素，并选择最大值。这些都是用来减少计算成本，并在一定程度上也减少了过拟合。

• 归一化层是一种正则化方法，可以加快收敛速度，控制并减少过拟合，同时还允许网络使用较大的学习率。

• Dropout 是一种正则化方法，其中某些层的部分节点被随机忽略（将其 wieghts 设置为零）。这将随机丢弃网络的一个属性，并强制网络以分布式方式学习特性。该方法还提高了泛化能力，减少了过拟合。

解决过拟合的方法可以看这个博客——深度学习100问之神经网络中解决过拟合的几种方法

• relu 是线性整流函数，又称修正线性单元，也就是俗称的激活函数，公式是 max（0，x）。relu 的主要作用就是向网络中添加非线性，故也称为非线性激活函数。

• Flatten 层用于将最终特征映射转换为一个一维向量，展开之后可以在某些 卷积/maxpool 层之后使用全连接层，它结合了以前卷积层提取的所有局部特征。

• 全连接（dense）层是用于实现分类，即人工神经网络分类器，在最后一层（Dense(10, activation='softmax')），网络输出每个类别的概率分布。

# 设置CNN模型
model = Sequential()

model.add(Conv2D(filters = 32, kernel_size = (5,5),padding = 'Same', 
                 activation ='relu', input_shape = (28,28,1)))
model.add(BatchNormalization())
model.add(Conv2D(filters = 32, kernel_size = (5,5),padding = 'Same', 
                 activation ='relu'))
model.add(BatchNormalization())
model.add(MaxPool2D(pool_size=(2,2)))
# model.add(Dropout(0.25))


model.add(Conv2D(filters = 64, kernel_size = (3,3),padding = 'Same', 
                 activation ='relu'))
model.add(BatchNormalization())
model.add(Conv2D(filters = 64, kernel_size = (3,3),padding = 'Same', 
                 activation ='relu'))
model.add(BatchNormalization())
model.add(MaxPool2D(pool_size=(2,2), strides=(2,2)))
# model.add(Dropout(0.25))


model.add(Flatten())
model.add(Dense(256, activation = "relu"))
model.add(Dropout(0.5))
model.add(Dense(10, activation = "softmax"))

# 输出模型各层的参数状况
model.summary()

3.2、设置优化器和退火函数

一旦网络模型构建成功，我们就需要有一个评分函数，一个损失函数和一个优化算法。

• 损失函数用来衡量模型在带有已知标签的图像数据集上的性能有多差，它是目标标签和预测标签之间的错误率。使用最多的是交叉熵损失函数，即 categorical_crossentropy loss。

• 优化器是最重要的功能，它将迭代地改进参数（filters kernel values, weights and bias of neurons ...），以最小化损失函数。

  • 可以选择 rmsprop，它是一个非常有效的优化器，以一种非常简单的方式调整 adagrad 方法，试图降低其攻击性强、单调下降的学习率。
  • 还可以使用 adam；
  • 也可以使用 sgd 优化器，但它比 rmsprop 慢。

• 度量函数 accuracy 用于评估模型的性能，不过仅用于评估。

# 用adam优化器和交叉熵损失进行编译
model.compile(optimizer="adam", loss="categorical_crossentropy", metrics=["accuracy"])

# 用sgd优化器
# model.compile(optimizer="sgd", loss="categorical_crossentropy", metrics=["accuracy"])

# 定义优化器
# optimizer = RMSprop(lr=0.001, rho=0.9, epsilon=1e-08, decay=0.0)
# 编译模型
# model.compile(optimizer = optimizer , loss = "categorical_crossentropy", metrics=["accuracy"])

为了使优化器更快地收敛，并且最接近全局最小损失函数， 这里使用了一种学习率（lr）的退火方法。lr 是学习率，它越高，步长越大，收敛速度越快。然而，由于 lr 较高，采样非常差，优化器可能会陷入局部极小值。所以可以在训练过程中降低学习率，以有效地达到损失函数的全局最小。为了保持计算速度快、lr 值高的优点，根据需要（在精度没有提高的情况下）每 x 步动态地减少 lr 值。

使用 keras.callbacks 中的 ReduceLROnPlateau 函数，如果在3个阶段之后精度没有提高，将 lr 减少一半。

# 设置一个学习率衰减
learning_rate_reduction = ReduceLROnPlateau(monitor='val_acc', 
                                            patience=3, 
                                            verbose=1, 
                                            factor=0.5, 
                                            min_lr=0.00001)

# 训练轮数，暂时设置为30，可以自己尝试调整
epochs = 30
# 批大小
batch_size = 86

3.3、数据增强

又称数据扩充/数据增广。

为了避免过拟合问题，需要对手写数字数据集进行人工扩充，它可以让你现有的数据集变得更大。这个想法最初是来源于用小的转换来改变训练数据，以重现某人在写一个数字时发生的变化，尤其适用于数据量较小的情况。以改变数组表示的方式改变训练数据，同时保持标签不变的方法称为数据增强技术。一些常用增强是灰度、水平翻转、垂直翻转、随机裁剪、颜色抖动、平移、旋转还有缩放等等。

通过数据增强可以轻松地将训练集的数量增加一倍或多倍，从而可以创建一个非常健壮的模型，因此这个改进很重要！！！

# 增加数据以防止过拟合
datagen = ImageDataGenerator(
        featurewise_center=False,  				# 在数据集上将输入平均值设置为0
        samplewise_center=False,  				# 将每个样本的平均值设置为0
        featurewise_std_normalization=False,    # 将输入除以数据集的std
        samplewise_std_normalization=False,  	# 将每个输入除以它的std
        zca_whitening=False,  					# 使用ZCA白化
        rotation_range=10,  					# 在范围内随机旋转图像（0到180度）
        zoom_range = 0.1, 						# 随机缩放图像
        width_shift_range=0.1,  				# 水平随机移动图像（总宽度的一部分）
        height_shift_range=0.1,  				# 垂直随机移动图像（总高度的一部分）
        horizontal_flip=False,  				# 随机翻转图像
        vertical_flip=False)  					# 随机翻转图像


datagen.fit(X_train)

为了增加数据选择了：

• 训练图像随机旋转10度；
• 随机缩放10%一些训练图像；
• 将图像水平移动10%的宽度；
• 将图像垂直移动10%的高度；
• 没有应用垂直翻转或水平翻转，因为它可能导致错误分类对称数字，如6和9。

3.4、拟合数据

一旦模型准备好了，就可以拟合训练数据集。

# 拟合模型
history = model.fit_generator(datagen.flow(X_train,Y_train, batch_size=batch_size),
                              epochs = epochs, validation_data = (X_val,Y_val),
                              verbose = 2, steps_per_epoch=X_train.shape[0] // batch_size,
                              callbacks=[learning_rate_reduction])

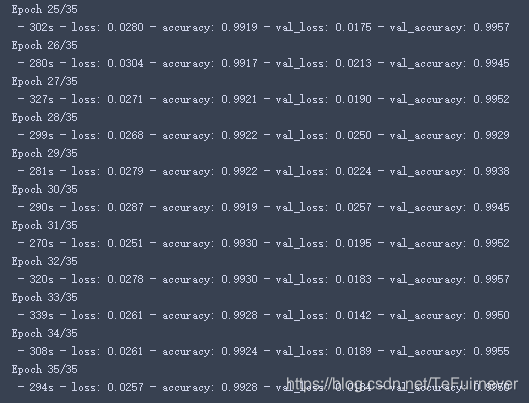
四、评估模型

4.1、训练和验证曲线

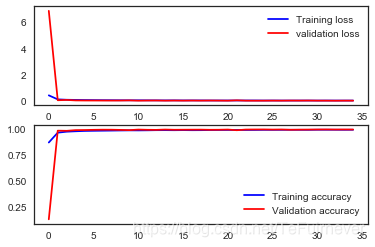
# 绘制训练和验证的损失和精度曲线
fig, ax = plt.subplots(2,1)
ax[0].plot(history.history['loss'], color='b', label="Training loss")
ax[0].plot(history.history['val_loss'], color='r', label="validation loss",axes =ax[0])
legend = ax[0].legend(loc='best', shadow=True)

ax[1].plot(history.history['accuracy'], color='b', label="Training accuracy")
ax[1].plot(history.history['val_accuracy'], color='r',label="Validation accuracy")
legend = ax[1].legend(loc='best', shadow=True)

4.2、混淆矩阵

混淆矩阵可以非常有助于了解模型缺点，所以绘制了验证结果的混淆矩阵。

# 看混淆矩阵
def plot_confusion_matrix(cm, classes,
                          normalize=False,
                          title='Confusion matrix',
                          cmap=plt.cm.Blues):
    """
    此函数打印并绘制混淆矩阵
	可以通过设置 “normalize=true” 应用归一化
    """
    plt.imshow(cm, interpolation='nearest', cmap=cmap)
    plt.title(title)
    plt.colorbar()
    tick_marks = np.arange(len(classes))
    plt.xticks(tick_marks, classes, rotation=45)
    plt.yticks(tick_marks, classes)

    if normalize:
        cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]

    thresh = cm.max() / 2.
    for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
        plt.text(j, i, cm[i, j],
                 horizontalalignment="center",
                 color="white" if cm[i, j] > thresh else "black")

    plt.tight_layout()
    plt.ylabel('True label')
    plt.xlabel('Predicted label')

# 从验证数据集中预测值
Y_pred = model.predict(X_val)
# 将预测类转换为一个独热向量
Y_pred_classes = np.argmax(Y_pred,axis = 1) 
# 将验证观测转换为一个独热向量
Y_true = np.argmax(Y_val,axis = 1) 
# 计算混淆矩阵
confusion_mtx = confusion_matrix(Y_true, Y_pred_classes) 
# 绘制混淆矩阵
plot_confusion_matrix(confusion_mtx, classes = range(10)) 

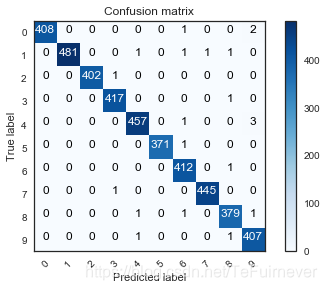
这里可以看到，CNN 在所有数字上都表现得非常好，考虑到验证集的大小（4200张图像），可以说错误是非常少的了。然而，也有一些麻烦，比如真实为4的数有好多被误分类为9。

来看看这些重要的错误，为了达到这个目的，需要得到结果中实际值和预测值的概率之间的差异。

# 显示一些错误结果

# 错误是预测标签和真实标签之间的区别
errors = (Y_pred_classes - Y_true != 0)

Y_pred_classes_errors = Y_pred_classes[errors]
Y_pred_errors = Y_pred[errors]
Y_true_errors = Y_true[errors]
X_val_errors = X_val[errors]

def display_errors(errors_index,img_errors,pred_errors, obs_errors):
    """
    此函数显示6个图像及其预测和实际标签
    """
    n = 0
    nrows = 2
    ncols = 3
    fig, ax = plt.subplots(nrows,ncols,sharex=True,sharey=True)
    for row in range(nrows):
        for col in range(ncols):
            error = errors_index[n]
            ax[row,col].imshow((img_errors[error]).reshape((28,28)))
            ax[row,col].set_title("Predicted label :{}
True label :{}".format(pred_errors[error],obs_errors[error]))
            n += 1

# 错误预测数的概率
Y_pred_errors_prob = np.max(Y_pred_errors,axis = 1)

# 误差集中真值的预测概率
true_prob_errors = np.diagonal(np.take(Y_pred_errors, Y_true_errors, axis=1))

# 预测标签概率与真实标签概率之差
delta_pred_true_errors = Y_pred_errors_prob - true_prob_errors

# 对预测标签概率与真实标签概率之差的列表进行排序
sorted_dela_errors = np.argsort(delta_pred_true_errors)

# Top 6错误
most_important_errors = sorted_dela_errors[-6:]

# 展示Top 6错误
display_errors(most_important_errors, X_val_errors, Y_pred_classes_errors, Y_true_errors)

最重要的错误也是最棘手的，对这六种情况，其中一些错误可能是由人类造成的，特别是对于一个非常接近 4 的 9，最后的9也很容易让人误解，对我来说似乎是0。

4.3、预测和提交

# 预测结果
results = model.predict(test)

# 选择最大概率的整数
results = np.argmax(results,axis = 1)
results = pd.Series(results,name="Label")

submission = pd.concat([pd.Series(range(1,28001),name = "ImageId"),results],axis = 1)

# 转换成CSV格式，不保留索引
submission.to_csv("cnn_mnist_datagen.csv",index=False)

随便跑了一次，结果还一般吧。

五、MNIST上的最佳模型

CNN的架构有很多选择，那么如何选择最好的一个呢？ 下面将会通过实验来进行测试。

下面是Kaggle排行榜得分的柱状图，每个栏的得分范围为0.1%：

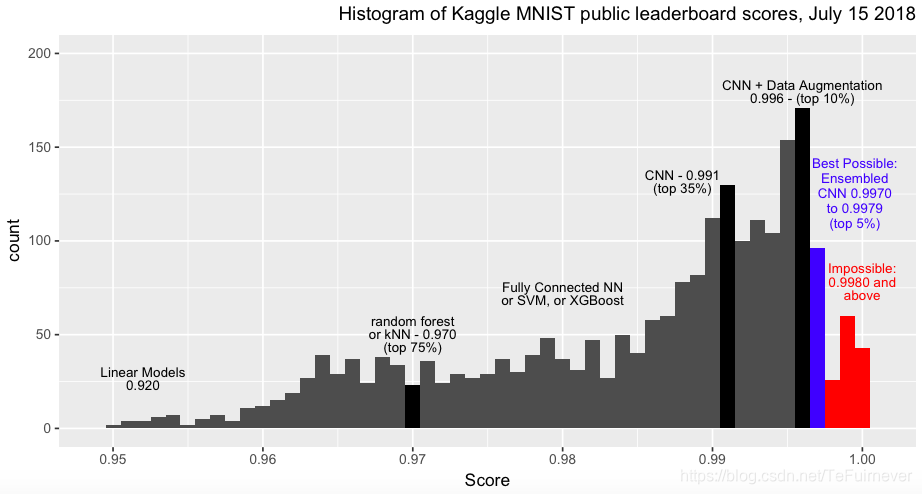
• 92％：多项逻辑回归又名 softmax 回归是简单的尝试，得分为 92％；
• 97％：非线性方法的得分为 97％，包括 kNN，随机森林等；
• 98％：非线性内核或全连接神经网络的 SVM 的得分为 98％，如果你调一调参，也许能到 99％；
• 99％：卷积神经网络是图像分类的冠军，基本跑几轮就得分 99％；

例如，model.add(Conv2D(filters=32,kernel_size=5,activation='relu'))，通过 Keras 实现的，带有 Dropout 的简单网络 784-32C5-500-10 在30轮后就可以达到了99％，如果添加一个池化层，它会在15轮内达到。

• 99.5％：一个设计好的CNN架构，然后添加了特殊功能，例如池化层，数据增强，Dropout，批归一化，学习率衰减，高级优化器等等，那么仅用20轮就可以突破 99.5％ 的里程碑！比如我们上面实验中使用的这个网络结构；
• 99.7%：要打破 99.7％，除了设计好的CNN架构，还要使用GPU，这样就不需要永远训练了，因为CPU跑的实在是太慢了！这种情况下，如果训练10次并进行10次结果提交，其中之一可能会超过 99.7％，因为每次训练CNN时，都会得到不同的结果；
• 99.8％-99.9％：要获得 99.8％ 或更高的分数，需要进行一次非常幸运的训练过程，或者需要使用 70,000 张图像的完整原始 MNIST 数据集进行训练，其中不公平地包含 Kaggle 的 test.csv 图像（这绝对是作弊），70,000 张图像的完整原始 MNIST 数据集的 地址在这；
  
• 100.0％：除了必须使用 70,000 张图像的完整原始MNIST数据集进行训练之外，还需要一个很好的算法支持，比如一个得分为 100％ 的Kaggle内核就是使用作弊算法 kNN。

六、不应该被提交的结果

使用 KNN k=1 和 MNIST 70k 图像，Accuracy=100%。

这个 kernel 就是一个不该做的例子，提交的结果在 Kaggle 的排行榜上得分 100%。

用 Kaggle 的 28000 张 test.csv 图像对 MNIST 的 70000 张原始数据集进行了 kNN k=1，以查看图像是否相同，结果验证了 Kaggle 未知的 test.csv 图像完全包含在 MNIST 的原始数据集中，并且具有已知的标签。因此，直接输出相应的标签，打包提交就可以实现得分 100% 了。。。。。。只说核心代码了，具体的直接 GitHub 上传了。

c1=0; c2=0;
print("Classifying Kaggle's 'test.csv' using kNN k=1 and MNIST 70k images")
for i in range(0,28000): 		# 循环Kaggle测试集
    for j in range(0,70000): 	# 循环MNIST数据集
    	# 如果数据相同，那么标签相同
        if np.absolute(Kaggle_test_image[i,] - MNIST_image[j,]).sum()==0:
            Kaggle_test_label[i] = MNIST_label[j]
            if i%1000==0:
                print("  %d images classified perfectly" % (i))
            if j<60000:
                c1 += 1
            else:
                c2 += 1
            break
if c1+c2==28000:
    print("  28000 images classified perfectly")
    print("Kaggle's 28000 test images are fully contained within MNIST's 70000 dataset")
    print("%d images are in MNIST-train's 60k and %d are in MNIST-test's 10k" % (c1,c2))

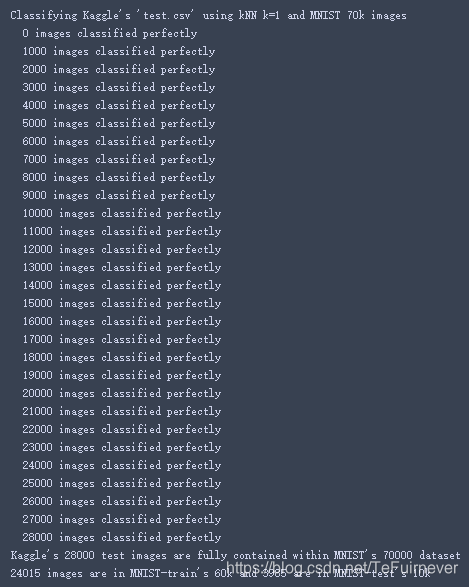
# 输出找到的标签即可
results = pd.Series(Kaggle_test_label.reshape(28000,),name="Label")
submission = pd.concat([pd.Series(range(1,28001),name = "ImageId"),results],axis = 1)
submission.to_csv("Do_not_submit",index=False)

使用 kNN k=1，我们能 100% 准确地知道 Kaggle 的前六个测试图像分别是数字2、0、9、0、3、7。同样，接下来的27994张测试图像也非常清楚。

这样的操作没有任何意义，不要这样做！！！

七、MNIST上的最佳CNN

https://www.kaggle.com/cdeotte/how-to-choose-cnn-architecture-mnist/notebook 中对【不同的卷积子空间对】、【特征图】、【全连接层】、【Dropout】、【归一化】、【数据增强】等等进行了分别的实验，发现了一下结构性能更高：

• 784(28 * 28) - [32C3-32C3-32C5S2](c=filter, s=stride) - [64C3-64C3-64C5S2] - 128 - 10
• 40% dropout，归一化，数据增强

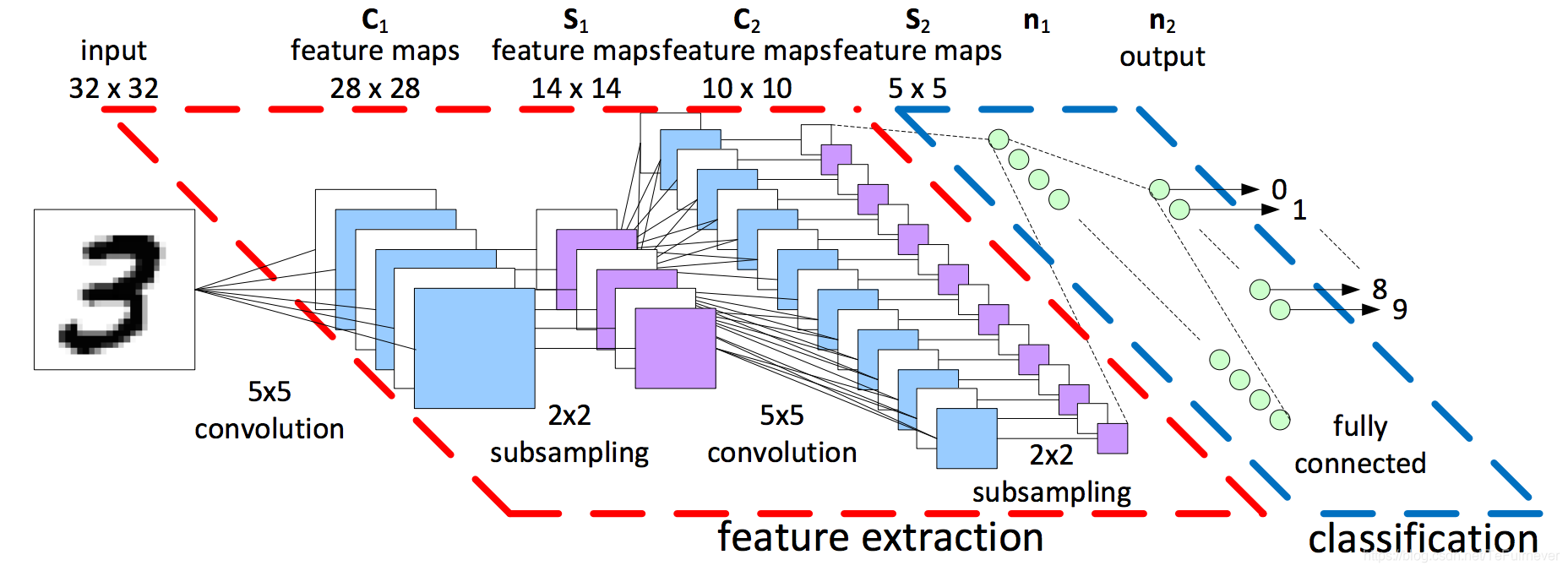
八、初代网络 LeNet-5

可以看到各个层的特征通过动画的形式表现出来了，现在 CNN 正在变得可视化，希望未来能摆脱黑盒子的称呼！！！

欢迎看一下这个高赞博客——大话卷积神经网络CNN（干货满满）。

九、GitHub

全部的代码和数据可以通过GitHub下载，地址是 https://github.com/TeFuirnever/Kaggle-Digit-Recognizer。

参考文章

• https://www.kaggle.com/kernels/svzip/notebook
• https://www.kaggle.com/cdeotte/how-to-choose-cnn-architecture-mnist/notebook
• https://www.kaggle.com/c/digit-recognizer/discussion/61480#latest-645703
• https://www.kaggle.com/cdeotte/mnist-perfect-100-using-knn/output#Accuracy=100%-using-kNN-k=1-and-MNIST-70k-images