运筹学那些事，专科学生学习运筹学，No.2

第三章：决策

决策的概念和程序

一堆背景和描述，读一遍即可

广义的决策过程应该包括四个程序：

1. 明确决策项目的目的
2. 寻求可行的方案
3. 在诸可行方案中进行抉择
4. 对选定的决策方案经过实施后的结果进行总结评价

决策的分类

（1）按决策方法不同而分类

1. 常规性决策 ：常规性决策是例行的、重复性的决策。
2. 特殊性决策：特殊性决策是对待特殊的、无先例可循的新问题的决策

（2）按计划和控制的关系分类

1. 计划性决策
2. 控制性决策

决策的程序

一个科学的决策全过程，包括四个步骤

1. 明确目标
2. 拟定多个可行方案（方案是否可行，需要进行可行性研究和系统分析）
3. 预测可能发生的自然状态，计算不同方案在不同的自然状态下的收益值（或损失值），编制决策收益表（损失表）

不确定条件下的决策

通过案例来解释

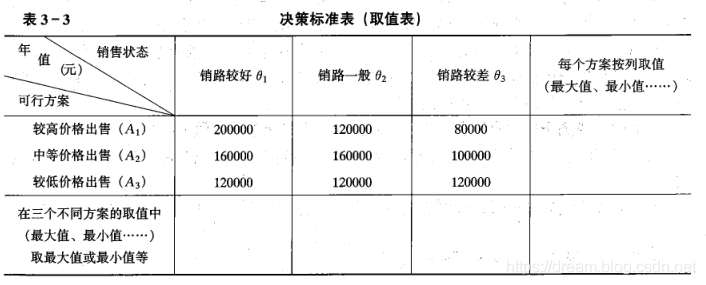
设某唱片和磁带录制公司计划录制一位新歌星的唱片，他们拟定的价格方案有三个：较高价格出售、中等价格出售、较低价格出售；他们估计唱片进入市场后，会出现的销售状态（自然状态）也有三种：即销路较好、销路一般、销路较差。根据以往的销售经验，他们计算出三个方案在三种不同的销售状态下的收益值（按下表），然后再运用不同的决策标准进行决策，选取最优的可行方案。

1） 最大最大决策标准

最大最大决策标准也可称为乐观主义者的决策标准，但是这种乐观不应是盲目乐观，应该是经过积极争取，大致上可以达到的最乐观的情况。

决策程序

首先从每个方案中选择一个最大的收益值，然后再从这些方案中选出的最大收益值中选择一个最大值，作为备选方案。
它的选择原则是大中取大，故又称其为最大最大标准

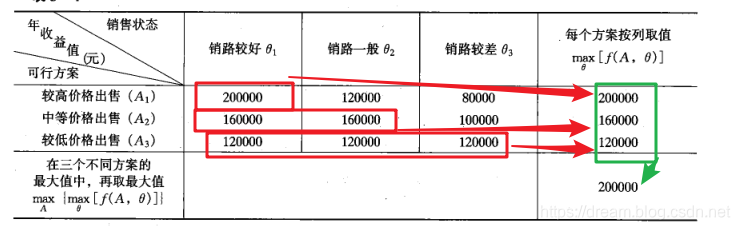
说白了，就是每个方案找最大值，然后在三个方案的最大值里面在取最大值

2）最大最小决策标准

最大最小决策标准也可以称为保守主义者的决策标准，采用这种决策标准，决策者比较谨慎小心。
悲观主义决策标准

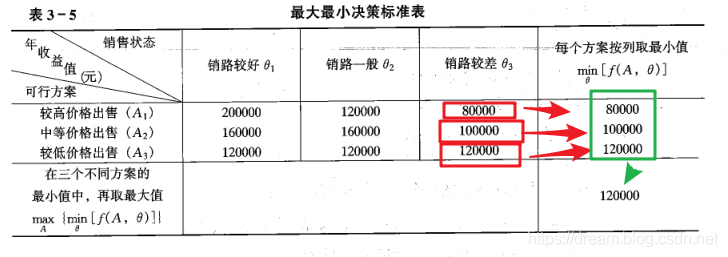
决策程序

首先从每一个方案中选择一个最小收益值，然后在从这些最小收益值所代表的不同方案中，选择一个收益值最大的方案作为备选方案。它的选择原则是小中取大，故称其为最大最小标准（奇怪，不应该是最小最大吗？？？）

3）最小最大遗憾值决策标准

这个小节有个概念需要记住
遗憾值（在近些年考察出现了2次）

在决策过程中，当某一种自然状态可能出现时，决策者必然首先要选择收益最大的方案，如果决策者由于决策失误未选取这一方案，而是选了其他方案，因为会感到遗憾而后悔，这两个方案的收益值之差叫遗憾值或者后悔值。
… 说白了，就是赔钱了！

看案例

1. 从决策收益表中标示不同状态下的最大收益值，如表所示
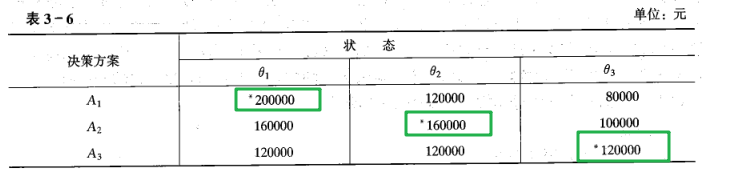
   绿色框里面是每列的最大值，注意是每列

2. 用每列附有“*”符号的最大收益值减去各个方案（每行的值），列出遗憾值表，如下表

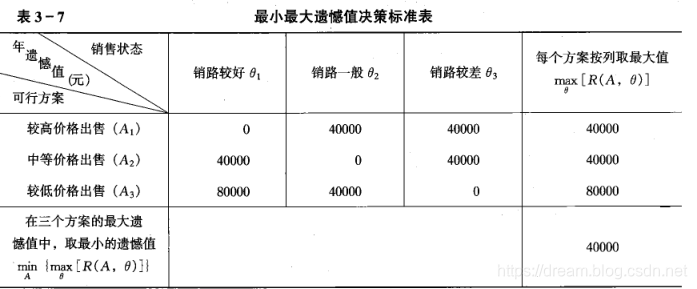
4）现实主义决策标准

现实主义决策标准也可以称为折中主义决策标准。

用大白话描述一下，就是给销路最好的概率定位α（这个α可以等于0~1之间的任意数字），然后销量最差的定为（1-α）
然后分别计算，计算完了，在取最大值即可

具体看教材即可，没有什么难度。

风险条件下的决策

风险情况下的决策一般又叫做统计型决策或随机决策，主要是根据多种不同的自然状态可能发生的概率来决策

概括起来，风险情况下的决策问题的条件是：

1. 有一个明确的决策目标，如收益最大或损失最小
2. 存在多个（两个以上）可行方案
3. 存在多个不以人们主观意志为转移的自然状态，并且每个自然状态可以估算出它的概率值
4. 不同可行方案在不同状态下的收益值或损失值可以定量计算出来

1）最大期望收益值标准

通过案例来说明

设有某书摊正在与某出版商联系订购下年度的挂历问题，已知的有关条件如下：挂历的零售价：80元/本（挂历上标明的名义价格），挂历的成本：50元/本（挂历的批发价格），书摊可得的毛利：30元/本（80元/本-50元/本），若当年12月31日以后挂历尚未售出时，该书摊不得不降价到20元/本出售，即只能收回部分成本（或叫挂历的折余值）。

在风险的条件下进行决策，一般常用的决策标准就是 期望利润标准，也叫贝叶斯标准。

步骤如下：

1. 确定概率值

售出本数	概率
150	0.1
160	0.2
170	0.4
180	0.3

2. 计算条件利润，所谓条件利润就是指某一利润的获得是以某一具体的购进方案遇到某一具体的销售数为条件的。

条件利润计算公式

上面这个公式如果一开始看起来别扭，不着急，看图计算一下就了解了

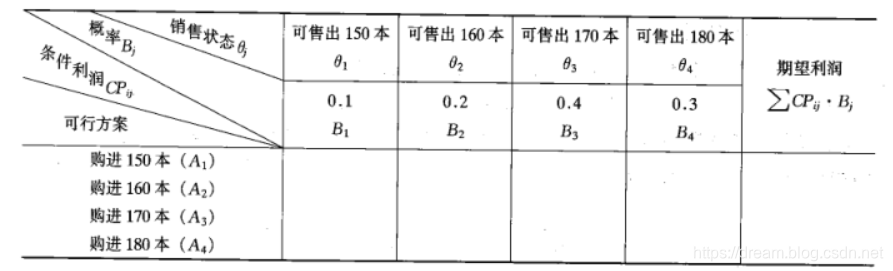
CP_1,2(购进状态为A₁，销售状态为θ₂的条件利润)，由于购进方案A₁是购进150本挂历，遇到的销售状态是θ₂是可以售出160本挂历，因此150本可以全部售出，可以获得的条件利润是

CP_1,2 = 30 * 150 = 4500 元

同理
CP_2,1 （购进160本，卖出150本）
CP_2,1 = 30150 - 5010+20*10 = 4200 元

依照相同的计算方法，计算全表，得到如下表所示

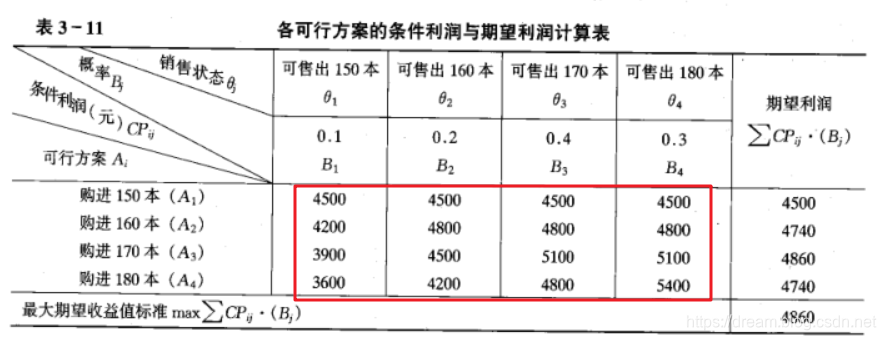
3. 计算各个方案的期望利润与选择最优方案。
各个方案的期望利润可按下式计算：


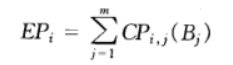
说白了，就是用算出的单元格的值，在乘以概率，去就期望利润

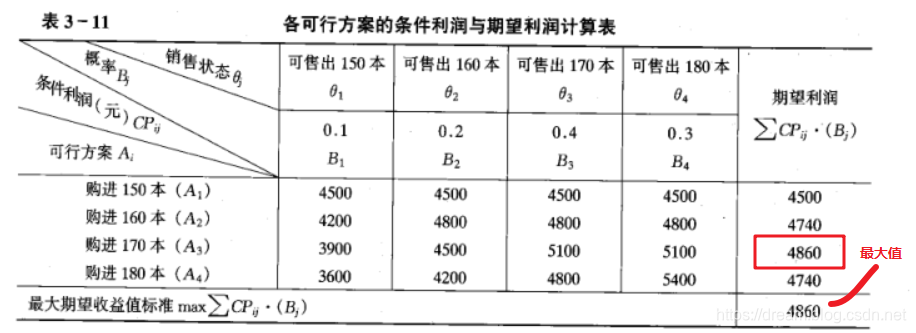
依据最大期望收益值标准，可以计算最大期望收益值。（不做赘述）

2）最小期望损失值标准

损失包括两部分报废损失 和 机会损失

计算所有状态的损失值，形成一个表

表内对角线上损失值为0，对角线的上部为机会损失，下部为报废损失

上表得到的170本（A₃）方案期望损失210元最小，为最优方案

决策树

决策树的结构

树是由方块和圆圈为结点，并由直线连接而成为一种树状结构。
方块结点是决策结点。
由决策点引出的树枝，称为方案枝，每个树枝代表一个方案。
圆圈结点是状态结点，由状态结点引出的树枝，称为状态枝，表示不同的状态。
在状态的末端列出不同状态下的收益值（或损失值），不同状态的概率值标示在状态枝的上部。

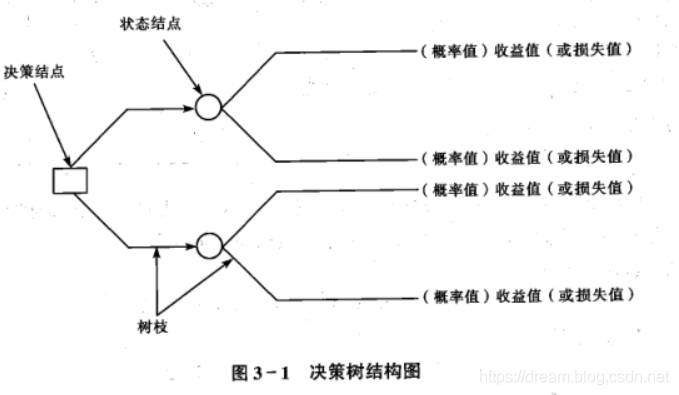
决策过程是由左向右，逐步后退，根据右端的收益值（或损失值）和状态枝上的概率值，计算出同一方案不同状态下的期望收益值（或期望损失值），然后根据不同方案的期望收益值大小进行决策。

方案的舍弃称为 修枝，舍弃的方案只需在枝上附以下面符号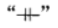
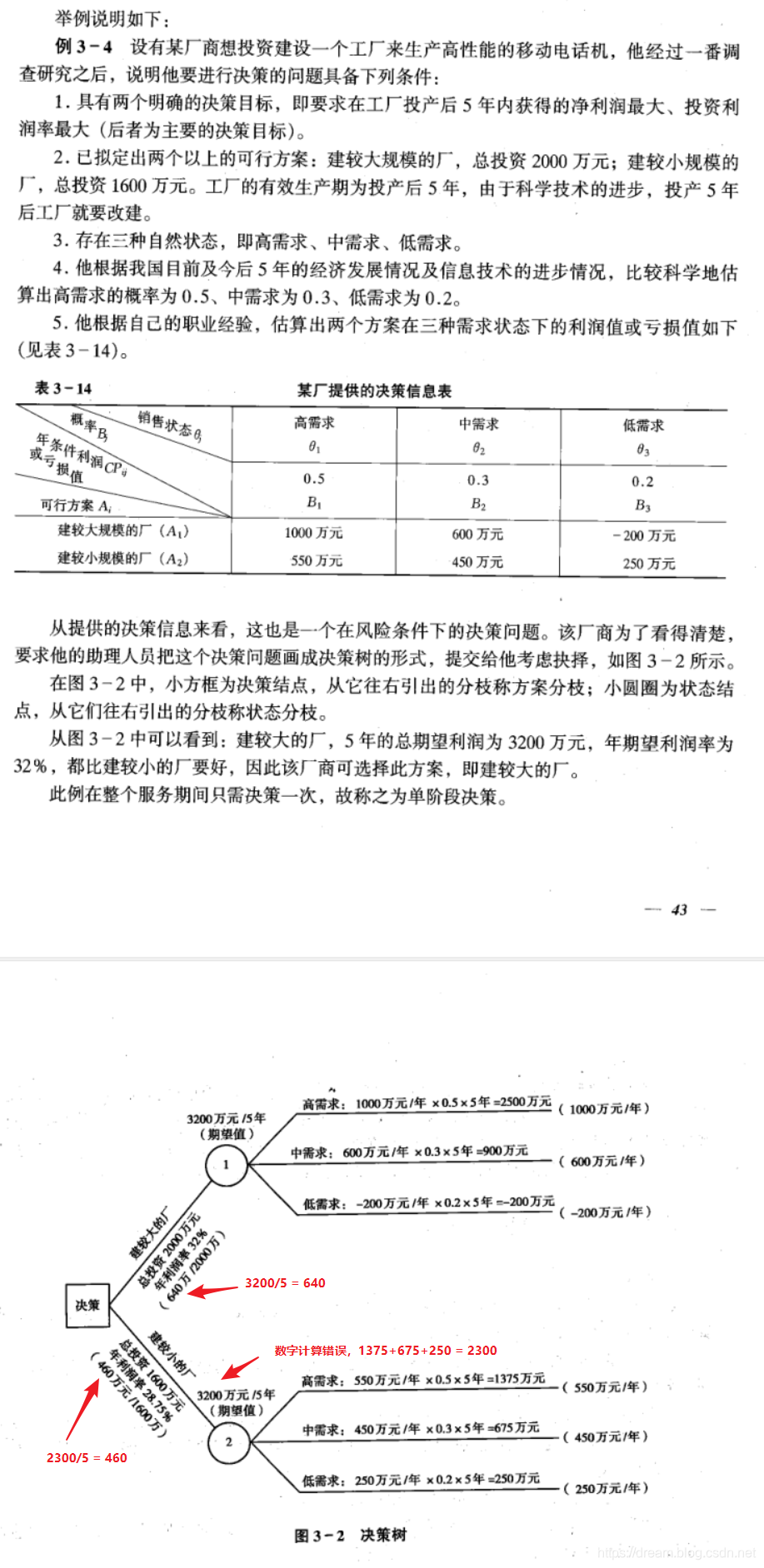
1）单阶段决策实例

参照案例即可，教材中有一个小计算错误，已经标注

2）多阶段决策实例

参考教材45页案例即可，看看就行。

决策树方法的优点

最后在吹吹牛即可

决策树方法已得到广泛的使用，它有五个明显的优点：

1. 它构成决策过程，使决策者能够以一种顺序的、有条理的方式接近决策。
2. 它要求决策者检验所有的可能的结果，合意的和不合意的一样要检验。
3. 它以一种非常简明的方式，把决策过程传给别人，说明对未来的每一种假设。
4. 通过集中注意于每一个财政数字、概率和优先的假设----一次一个，以便分组来讨论各种方案。
5. 它能够和计算机一起使用，为的是可以模拟许多不同组合的假设，来观察这些供选择的方案中各种改变的最终结果所产生的影响。

决策树能够形象地显示出整个决策问题在时间上或决策顺序上的不同阶段的决策过程，特别是应用于复杂的多阶段决策。层次清楚，阶段明显，有利于决策机构做出正确的决策。

自考必看

然后，重点来了，附件给一份名词解释题，近20年的

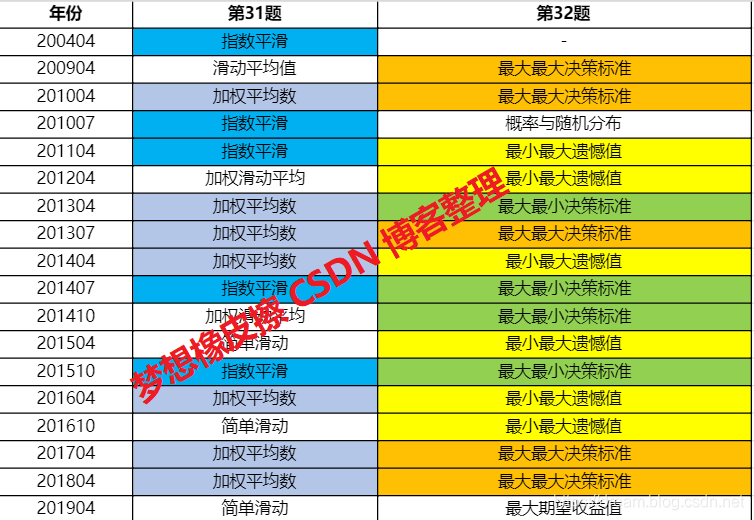
还有一句话要说：运筹学，自考卷，第32题，一般考察 决策，例如最大最大决策标准，最大最小决策标准。

这20年计算题考察表格，完善中