
其实这套题很好。
但是这次,在T1爆炸的同时,T2和T3并没有出现能弥补的表现。
在AK仍然存在的同时,我居然连一个AC都没有。
所以最后就是一无是处的一场。
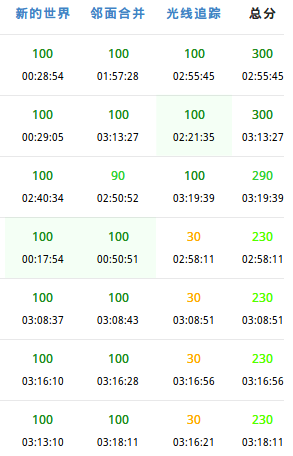
考试结束前估分:100+100+30=230
结果T1和T2都没有A。。。
T1乖乖的按照题意打大模拟,没算复杂度,开心的一匹。。。
T2位运算判定锅了,判断两个数二进制下的某几位是否相同不能与运算完再与原数判。
看到这句红色加粗的话我自己也想笑了。。。怎么能做到这么蠢的啊。。?
思路倒是对的,炸了50分。
T3想到线段树的正解,但是感觉会严重炸精把线段树弄成炸精树,后来就开始yy题目里的八分树。
还有一个小时10分钟的时候我打完了T1T2然后T3的30分暴力也写完了。
此时脑子里有一个不能让自己相信的正解,以及不是很放心的T1T2。
很凌乱,然后我在再写30分的部分分和尝试打T3正解和检查T1T2之间徘徊。
但是这次T1T2没办法对拍(没有暴力。。。)
最后什么都没有干成。剩15分钟的时候决心打30部分分,结果没调出来。
菜,还是菜。
这一轮可能又要废了。。。。。
哎,还是少一点废话吧。。。也改变不了什么。。。
T1:新的世界
转化题意,是最短路。
不难发现更新的先后顺序与答案无关。
出题人精心构造数据,直接模拟T死,反顺序dfs能极快AC。。。
唉。。。

1 #include<cstdio> 2 #include<iostream> 3 #include<queue> 4 using namespace std; 5 int n,m,A[505][505],L[505][505],r,c,l; 6 const int xx[4]={0,0,1,-1}; 7 const int yy[4]={1,-1,0,0}; 8 #define tx x+xx[i] 9 #define ty y+yy[i] 10 struct P{ 11 int x,y,dt; 12 friend bool operator<(P a,P b){ 13 return a.dt<b.dt; 14 } 15 }; 16 priority_queue<P>q; 17 int main(){ 18 scanf("%d%d",&n,&m); 19 for(int i=1;i<=n;++i)for(int j=1;j<=m;++j)scanf("%d",&A[i][j]); 20 scanf("%d%d%d",&r,&c,&l); L[r][c]=l; q.push((P){r,c,l}); 21 for(int i=1;i<=n;++i)A[i][0]=A[i][m+1]=1234567890; 22 for(int i=1;i<=m;++i)A[0][i]=A[n+1][i]=1234567890; 23 scanf("%d%d",&r,&c); 24 while(!q.empty()){ 25 int x=q.top().x,y=q.top().y,dt=q.top().dt;q.pop(); 26 if(x==r&&y==c)return printf("%d ",dt),0; 27 for(int i=0;i<4;++i)if(L[tx][ty]<dt-A[tx][ty]) 28 q.push((P){tx,ty,L[tx][ty]=dt-A[tx][ty]}); 29 }puts("0"); 30 }
T2:邻面合并
采用8进制压位,一共8*3+1=25位
其中8个8进制数表示以某一个点为起点的连续段终点是几。
1~7分别对应2~8而终点是1的情况与该起点不存在的情况无法区分。
那么如果存在终点是1的话起点一定是1,特判,如果存在终点为1的话,那么就把状态数+(1<<24)
搜索得到,状态数只有1597个,不均匀的分布在256种限制里。
预处理两种状态之间转移的费用。枚举上下两层的决策即可。

1 #include<cstdio> 2 #include<vector> 3 #include<cstring> 4 #include<iostream> 5 using namespace std; 6 vector<int>v[257]; 7 int ss[9],se[9],tp,cnt,ref[1605],L[257],R[257]; 8 int fee[1605][1605],dp[105][1605],st[102],ans=1234567890,n,m,x; 9 void sch(int c){ 10 int s=0,fs=0; 11 for(int i=1;i<=tp;++i)for(int j=ss[i];j<=se[i];++j)s|=1<<j-1; 12 for(int i=1;i<=tp;++i)fs|=se[i]-1<<3*ss[i]-3; 13 if(tp&&ss[1]==1&&se[1]==1)fs|=1<<24; 14 v[s].push_back(fs); 15 for(int s=c+1;s<=8;++s)for(int e=s;e<=8;++e)ss[++tp]=s,se[tp]=e,sch(e),tp--; 16 } 17 int main(){ 18 sch(0); 19 for(int i=0;i<256;++i){ 20 L[i]=cnt+1; 21 for(int j=0;j<v[i].size();++j)ref[++cnt]=v[i][j]; 22 R[i]=cnt; 23 } 24 for(int i=1;i<=cnt;++i)for(int j=1;j<=cnt;++j){ 25 int s=ref[j],sp=ref[j]; 26 for(int t=9;t;--t,s>>=3)if(s&7)fee[i][j]++; 27 s=ref[i]; 28 for(int t=9;t;--t,s>>=3,sp>>=3)if(s&7)if((s&7)==(sp&7))fee[i][j]--; 29 } 30 memset(dp,30,sizeof dp); dp[0][1]=0; 31 scanf("%d%d",&n,&m); 32 for(int i=1;i<=n;++i)for(int j=1;j<=m;++j)scanf("%d",&x),st[i]|=x<<j-1; 33 for(int i=1;i<=n;++i)for(int j=L[st[i-1]];j<=R[st[i-1]];++j) 34 for(int k=L[st[i]];k<=R[st[i]];++k) 35 dp[i][k]=min(dp[i][k],dp[i-1][j]+fee[j][k]); 36 for(int i=L[st[n]];i<=R[st[n]];++i)ans=min(ans,dp[n][i]); 37 printf("%d ",ans); 38 }
T3:光线追踪
可以发现,每一个矩形生效的只有左,下两条边。
一条边当然在一段连续的角度露出。
在一个角度下多条边,被看到的一定是横/纵坐标最小的。
如果坐标相同,那么编号大的更优。
然后就是维护结构体的区间修改单点查询了。
对于横着和竖着的边分开维护,两个线段树即可(当然结构体封装。。。)
但是线段树当然不能基于浮点数,不然绝对就是个炸精树
所以把所有要用到的浮点数都算出来,sort+unique离散化
用long double 就不会炸精,做乘除是用1.0l而不是1.0(Paris和kx的exp)
特殊处理x=0和y=0,方法很多。
我的方法是存下所有x=0,y=0的点的当前最小的另一个坐标以及编号。
同时,x=0的不能直接放进树里因为算角度时除0会爆炸。
但是我们也不能把它直接扔掉不管因为0~rx的那一段横着的线段可能还有用。
所以我们把它强制设定为1e-7而不是0就好了。
其实没有那么难码。真心祝愿你不要炸精。

1 #include<cstdio> 2 #include<algorithm> 3 #include<iostream> 4 using namespace std; 5 int opt[100005],ux[100005],uy[100005],dx[100005],dy[100006],tp,n,mnx0=1e9+7,mnxo,mny0=1e9+7,mnyo; 6 long double r[300005]; 7 struct P{int ord,x;}; 8 P Max(P a,P b){return a.x<b.x?a:(a.x==b.x?(a.ord<b.ord?b:a):b);} 9 int G(int p){return p>1000000000?0:p;} 10 struct Segment_Tree{ 11 int cl[6666666],cr[6666666];P w[6666666]; 12 void build(int p,int l,int r){ 13 cl[p]=l;cr[p]=r;w[p]=(P){1000000001,1000000001}; 14 if(l==r)return; 15 build(p<<1,l,l+r>>1); 16 build(p<<1|1,(l+r>>1)+1,r); 17 } 18 void set(int p,int l,int r,int ord,int x){ 19 if(l<=cl[p]&&cr[p]<=r)return w[p]=Max(w[p],(P){ord,x}),(void)0; 20 if(l<=cr[p<<1])set(p<<1,l,r,ord,x); 21 if(r>=cl[p<<1|1])set(p<<1|1,l,r,ord,x); 22 } 23 P ask(int p,int pos){ 24 if(cl[p]==cr[p])return w[p]; 25 return Max(w[p],pos<=cr[p<<1]?ask(p<<1,pos):ask(p<<1|1,pos)); 26 } 27 }X,Y; 28 main(){//freopen("raytracing4.in","r",stdin);freopen("my.out","w",stdout); 29 scanf("%d",&n); 30 for(int i=1;i<=n;++i){ 31 scanf("%d",&opt[i]); 32 if(opt[i]==1){ 33 scanf("%d%d%d%d",&dx[i],&dy[i],&ux[i],&uy[i]); 34 if(dx[i])r[++tp]=1.0L*dy[i]/dx[i],r[++tp]=1.0L*uy[i]/dx[i],r[++tp]=1.0L*dy[i]/ux[i]; 35 else r[++tp]=dy[i]/1e-7L,r[++tp]=uy[i]/1e-7L,r[++tp]=dy[i]/ux[i]; 36 } 37 else { 38 scanf("%d%d",&dx[i],&dy[i]); 39 if(dx[i])r[++tp]=1.0L*dy[i]/dx[i]; 40 } 41 }sort(r+1,r+1+tp);tp=unique(r+1,r+1+tp)-r-1; 42 X.build(1,1,tp);Y.build(1,1,tp); 43 for(int i=1;i<=n;++i)if(opt[i]==1){ 44 if(!dx[i])if(mnx0>=dy[i])mnx0=dy[i],mnxo=i; 45 if(!dy[i])if(mny0>=dx[i])mny0=dx[i],mnyo=i; 46 int x1=lower_bound(r+1,r+1+tp,1.0L*dy[i]/(dx[i]?dx[i]:1e-7L))-r, 47 x2=lower_bound(r+1,r+1+tp,1.0L*uy[i]/(dx[i]?dx[i]:1e-7L))-r, 48 x3=lower_bound(r+1,r+1+tp,1.0L*dy[i]/ux[i])-r; 49 X.set(1,x1,x2,i,dx[i]); Y.set(1,x3,x1,i,dy[i]); 50 }else{ 51 if(!dx[i]){printf("%d ",mnxo);continue;} 52 if(!dy[i]){printf("%d ",mnyo);continue;} 53 P a1=X.ask(1,lower_bound(r+1,r+1+tp,1.0L*dy[i]/dx[i])-r), 54 a2=Y.ask(1,lower_bound(r+1,r+1+tp,1.0L*dy[i]/dx[i])-r); 55 int fx=a1.x,fy=a2.x; 56 if(1ll*fx*dy[i]==1ll*fy*dx[i])printf("%d ",G(max(a1.ord,a2.ord))); 57 else if(1ll*fx*dy[i]<1ll*fy*dx[i])printf("%d ",G(a1.ord)); 58 else printf("%d ",G(a2.ord)); 59 } 60 }
