启发式搜索
1. 相关概念
- 在宽度优先和深度优先搜索里面,我们都是根据搜索的顺序依次进行搜索,可以称为盲目搜索,搜索效率非常低。
- 而启发式搜索则大大提高了搜索效率,由这两张图可以看出它们的差别:
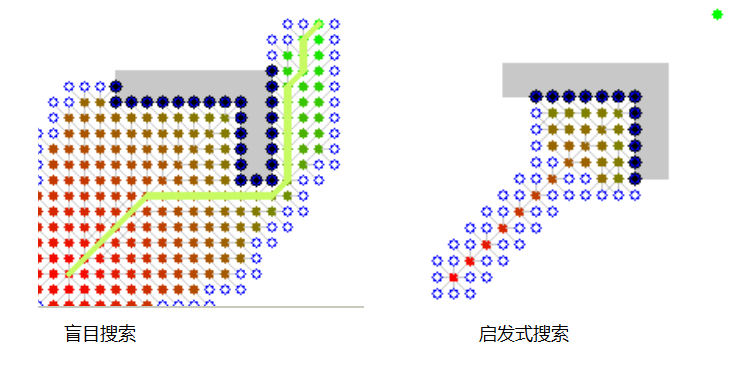
什么是启发式搜索(heuristic search)
-
用当前与问题有关的信息作为启发式信息,这些信息是能够提升查找效率以及减少查找次数的。
-
我们定义了一个估价函数 h(x) 用于估计状态 x 到 终点 的 代价
起始状态到
x状态所花的代价,我们称为g(x)
令F(x)=g(x)+h(x),作为我们的搜索依据。
你要从x走到目的地,那么 h(x) 就是你感觉或者目测大概要走的距离,h*(x) 则是你到达目的地后,发现你实际走了的距离。你预想的距离一定是比实际距离短,或者刚好等于实际距离的值。这样我们称你的 h(x) 是可纳的,是乐观的。
2. A*图示过程
-
方格左下角为
G(x)为起点到x的步数,右下角为H(x)为x到终点的预估值,这里选的是曼哈顿距离,右上角为F(x)=G(x)+H(x)估价函数。绿色点为起点,黑点为墙,红点为终点。起点相邻四个点进open表,并计算出F值。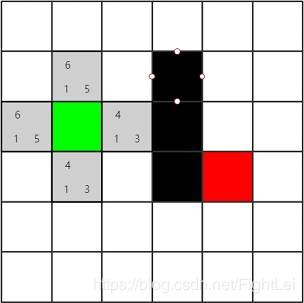
-
继续选择
open列表中F值最小的节点,此时最小节点有两个,都为4。这种情况下选取哪一个都是一样的,不会影响搜索算法的效率。因为启发式相同。这个例子中按照右下左上的顺序选取。先选择绿色节点右边的节点为当前节点,并将其加入close列表。其相邻4个节点中,有1个是黑色节点不可达,绿色节点已经被加入close列表,还剩下上下两个相邻节点,分别计算其F值,并设置他们的父节点为黄色节点。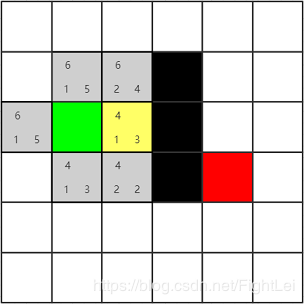
-
此时
open列表中F值最小为4,继续选取下方节点,计算其相邻节点。其右侧是黑色节点,上方1号节点在close列表。下方节点是新扩展的。主要来看下左侧节点,它已经在open列表中了。根据算法我们要重新计算它的F值,按经过2号节点计算G(n) = 3,H(n)不变,所以F(n) = 6相比于原值反而变大了,所以什么也不做。(后面的步骤中重新计算F值都不会更小,不再赘述)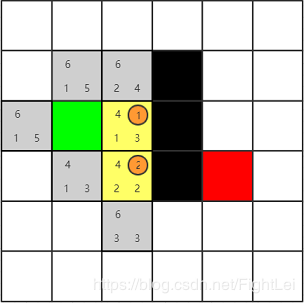
-
此时
open列表中F值最小仍为4,继续选取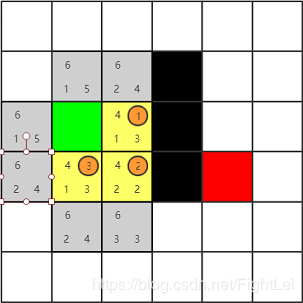
-
此时
open列表中F值最小为6,优先选取下方节点。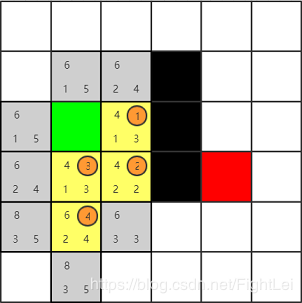
-
此时
open列表中F值最小为6,优先选取右方节点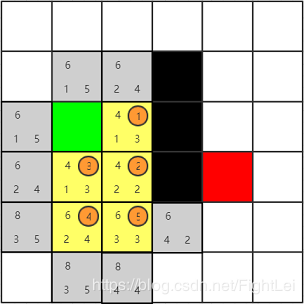
-
此时
open列表中F值最小为6,优先选取右方节点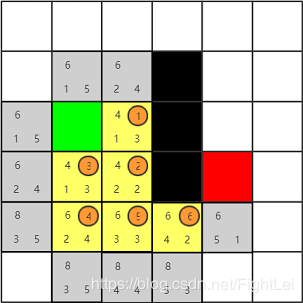
-
此时
open列表中F值最小为6,优先选取右方节点。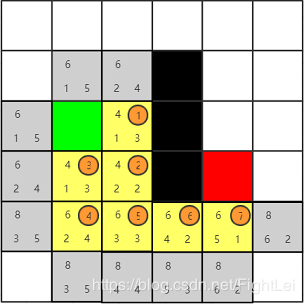
-
此时我们发现红色节点已经被添加到
open列表中,算法结束。从红色节点开始逆推,其父节点为7号,7号父节点为6号,6号父节点为5号,5号父节点为2号(注意这里5号的父节点是2号,因为5号是被2号加入到open列表中的,且一直未被更新),2号父节点为1号,最终得到检索路径为:绿色-1-2-5-6-7-红色。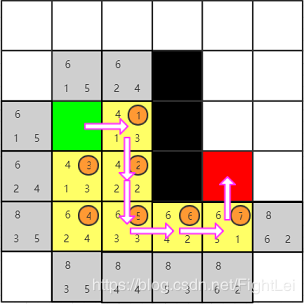
#include<bits/stdc++.h>
using namespace std;
const int maxn = 1e4+10;
struct node{
int x, y, fx;
node(int a, int b, int c){ x = a, y = b, fx = c; }
bool operator < (const node &a) const{ return a.fx < fx; }
};
int dx[] = {0, -1, 0, 1}, dy[] = {-1, 0, 1, 0};
int a[maxn][maxn], f[maxn], g[maxn][maxn], vis[maxn][maxn];
int n, m, k, sx, sy, ex, ey;
int h(int x, int y){ return abs(x - ex) + abs(y - ey); }//估价函数
int Astar(){
memset(g, 0x3f, sizeof(g));
g[sx][sy] = 0;
priority_queue<node> q;
q.push(node(sx, sy, h(sx, sy)));
while(!q.empty()){
node now = q.top(); q.pop();
vis[now.x][now.y] = 1;
for(int i=0; i<4; i++){
int x = now.x + dx[i], y = now.y + dy[i];
if(x<1 || y<1 || x>m || y>n || vis[x][y] || a[x][y]) continue;
if(g[x][y] > g[now.x][now.y] + 1) g[x][y] = g[now.x][now.y] + 1;
else continue;
if(x==ex && y==ey) return g[x][y];
q.push(node(x, y, g[x][y] + h(x, y)));
}
}
}
int main(){
scanf("%d%d%d%d%d%d%d", &n, &m, &k, &sx, &sy, &ex, &ey);
for(int i=1; i<=k; i++){
int x, y; scanf("%d%d", &x, &y);
a[x][y] = 1;
}
printf("%d
", Astar());
return 0;
}