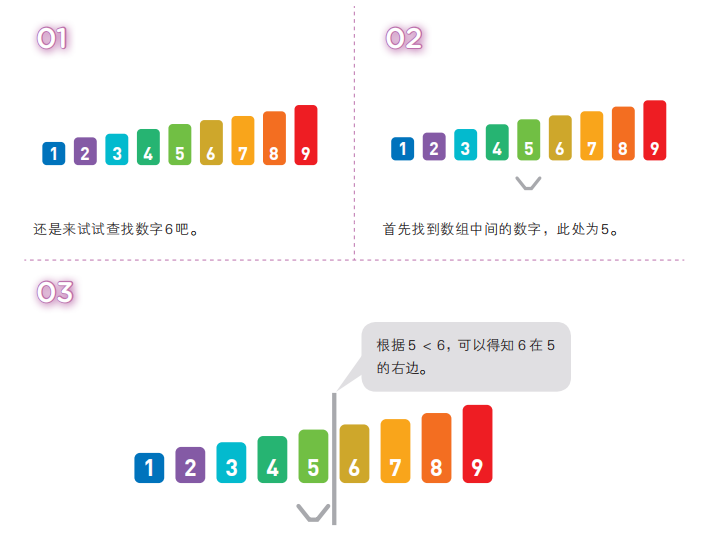
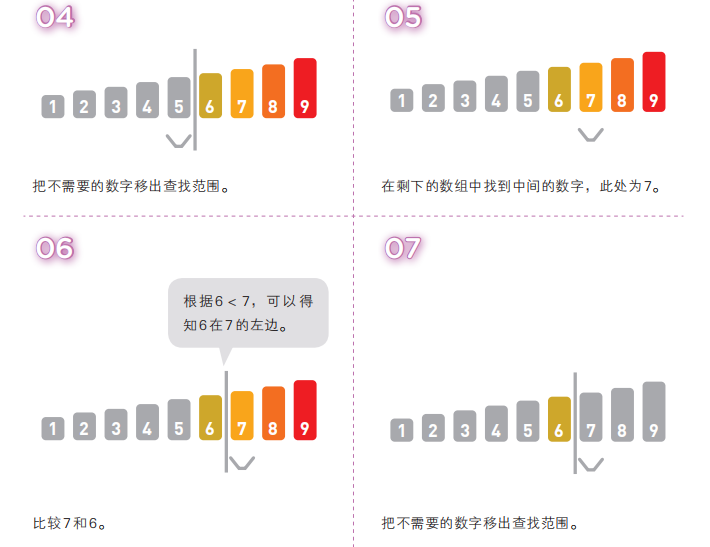
二分查找也是一种在数组中查找数据的算法。和线性查找不同,它只能查找已经排好序的数据。二分查找通过比较数组中间的数据与目标数据的大小,可以得知目标数据是在数组的左边还是右边。因此,比较一次就可以把查找范围缩小一半。重复执行该操作就可以找到目标数据,或得出目标数据不存在的结论。

解说
二分查找利用已排好序的数组,每一次查找都可以将查找范围减半。查找范围内只剩一个数据时查找结束。数据量为 n 的数组,将其长度减半 log2n 次后,其中便只剩一个数据了。也就是说,在二分查找中重复执行“将目标数据和数组中间的数据进行比较后将查找范围减半”的操作 log2n 次后,就能找到目标数据(若没找到则可以得出数据不存在的结论),因此它的时间复杂度为 O(logn)。
补充说明
二分查找的时间复杂度为 O(logn),与线性查找的 O(n) 相比速度上得到了指数倍提高(x=log2n,则 n=2x)。但是,二分查找必须建立在数据已经排好序的基础上才能使用,因此添加数据时必须加到合适的位置,这就需要额外耗费维护数组的时间。而使用线性查找时,数组中的数据可以是无序的,因此添加数据时也无须顾虑位置,直接把它加在末尾即可,不需要耗费时间。综上,具体使用哪种查找方法,可以根据查找和添加两个操作哪个更为频繁来决定。