如果一个处处可导的函数的图像和一条水平直线交于不同的两点(如图所示),
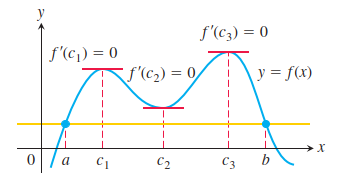
那么在这两点间的函数图像上至少存在一点处的切线平行于该水平直线(显然也平行于x轴),这种现象可以更严谨地表述为罗尔定理(Rolle’s Theorem[1]):如果函数f(x)在[a,b]上连续,(a,b) 上可导,并且f(a)=f(b),那么至少存在一点c于(a,b)内使得f’(c)=0。
上面说到的平行关系在罗尔定理中是这样体现的:因为f(a)=f(b),所以(a,f(a))和(b,f(b))可以确定一条水平直线,因为f’(c)=0,所以函数f(x)在(c,f(c))处的切线也是一条水平直线,很显然这两条直线平行。
罗尔定理的证明要求的是关于导数等于0的结论,我想到的是:(1)如果f(x)是常数函数的话,那么定义域内任意一点的导数都为0;(2)可导的函数在极值点处导数为0。所以这里证明的难点是:如果f(x)不是常数函数,那么该怎么证明其有极值存在于(a,b)内呢?若能证明之,则罗尔定理得证。如果f(x)不是常数函数,因为f(x)在[a,b]上连续,那么在该区间上面必然存在极大值和极小值,假设极大值和极小值均在端点处取得,再加上本定理的条件已经声明f(x)在两端点处的值相等(即f(a)=f(b)),可得出这种情况下函数的极大值等于极小值,这样的函数显然是常数函数,这与开头的假设“f(x)不是常数函数”相悖,所以f(x)不是常数函数情况下其极大值和极小值不可能都在端点处取得——至少存在一个极值点于(a,b)内,又因为f(x)在 (a,b) 上可导,所以该处函数导数为0。下面是我的证明过程:因为f(x)在[a,b]上连续,那么在该区间上面必然存在极大值和极小值。其极值的分布情况只有两种可能:(1)若f(x)的极值至少有一个在(a,b)内取得,设该极值点的横坐标为c,因为f(x)在 (a,b) 上可导,所以有f’(c)=0;(2)若f(x)的极值均不在(a,b)内取得——极值均在端点处取得,这两个极值分别是f(a)和f(b),由于本定理的条件中已经声明f(x)在两端点处的值相等(即f(a)=f(b)),可知函数的极大值等于极小值,这样的函数显然是常数函数,那么于(a,b)内的任何一点c都有f’(c)=0。综上,至少存在一点c于(a,b)内使得f’(c)=0,罗尔定理得证。
上面的证明思路和我分析问题的思路是有差别的,证明过程是对我分析问题的思路的整合与升华,借此顺便一提:书上的证明过程未必和我们解决问题的思路一致,诸位留意!
罗尔定理要求“函数f(x)在[a,b]上连续,(a,b) 上可导”,这两个条件总让我感觉有些憋扭,因为f(x)在 (a,b) 上可导的话就一定可得出f(x)在 (a,b) 上连续,于是可把条件转化为“函数f(x)在(a,b) 上可导,在a、b两点处连续”,但感觉还是不够简洁,为什么不直接把条件简单地限制为“函数f(x)在[a,b]上可导”呢?在这个条件下一定会有“函数f(x)在[a,b]上连续,(a,b) 上可导”,后来我想到不做这种简化的原因可能是:函数在a、b两端点处的导数可能是+∞或-∞——不可导,在这种情况下如果把“函数f(x)在[a,b]上连续,(a,b) 上可导”简化成“函数f(x)在[a,b]上可导”就会使罗尔定理不适用于下面这种情况[2](该函数在-1和1处不可导):
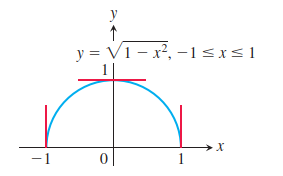
认识到这种情形之后,我们可以有一个适用范围小一点但同时也更简洁的罗尔定理:如果函数f(x)在[a,b]上可导,并且f(a)=f(b),那么至少存在一点c于(a,b)内使得f’(c)=0。
如果函数f(x)在[a,b]上不连续,那么罗尔定理可能不成立,如图所示:
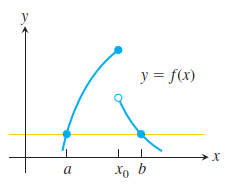
如果函数f(x)在(a,b)上不可导,那么罗尔定理可能不成立,如图所示:
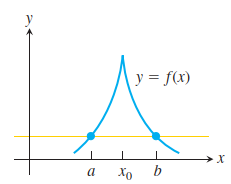
上面两图意在让各位认识到罗尔定理的成立条件的必要性。
若一条直线和处处可导的函数f(x)的图像交于(a,f(a))和(b,f(b))两点,将该直线上下平移,那么总存在该直线和函数f(x)的图像相切的情形,

这种现象可以更严谨地表述为微分中值定理(亦称拉格朗日中值定理,the mean value theorem of the differential calculus):如果函数f(x)在[a,b]上连续,(a,b) 上可导,那么至少存在一点c于(a,b)内使得(f^{'}left( c ight) = frac{f(b) - f(a)}{b - a})。
微分中值定理可以看作是罗尔定理旋转后的情形[3]——可设想把满足罗尔定理的图像旋转一个角度后,那么原来过(a,f(a))和(b,f(b))的水平直线变成了斜率为(frac{f(b) - f(a)}{b - a})的直线,而那条切线始终与之平行,所以斜率(该点的导数)依然等于(frac{f(b) - f(a)}{b - a})。
微分中值定理也可以用罗尔定理来证明,如下:
过(a,f(a))和(b,f(b))的直线的方程是(gleft( x ight) = fleft( a ight) + frac{fleft( b ight) - fleft( a ight)}{b - a}(x - a)),f(x)和g(x)的纵向差距可表示为(hleft( x ight) = fleft( x ight) - gleft( x ight) = fleft( x ight) - fleft( a ight) - frac{fleft( b ight) - fleft( a ight)}{b - a}(x - a)),因为f(x)和g(x)的图像在两端点处相交,所以h(a)=h(b)=0,同时不难得出h(x)在[a,b]上连续,(a,b) 上可导,所以h(x)满足罗尔定理,因而存在一点c于(a,b)内使得(h’(c) = 0 = f'left( c ight) - frac{fleft( b ight) - fleft( a ight)}{b - a}),进而可得出(f^{'}(c) = frac{fleft( b ight) - fleft( a ight)}{b - a}),微分中值定理得证。
作为微分中值定理的应用,我们可以考虑这样一种情形:假如一辆车做变速运动,一小时行了20km,如果f(x)是车的位移函数、f(0)=0、f(1)=20,微分中值定理告诉我们在这一小时内必然有一刻车速为(frac{fleft( 1 ight) - fleft( 0 ight)}{1 - 0} = frac{20 - 0}{1 - 0} = 20(km/h))。如果你对此仍怀疑,那么请设想其反面:若这一小时内车速始终大于或小于20km/h会出现什么情况?……所以这一小时内车速绝对会有一刻为20km/h。
对比一下微分中值定理和罗尔定理的差异,我们不难发现微分中值定理可以囊括罗尔定理的情形——微分中值定理中f(a)=f(b)的时候它便退化成了罗尔定理,也就是说微分中值定理具有更普遍的适用范围。现在让我们来看一个更广义的微分中值定理[4](亦称柯西中值定理,Generalized Mean Value Theorem of the Differential Calculus):如果f(x)和g(x)都在[a,b]上连续,(a,b) 上可导,那么至少存在一点c于(a,b)内使得
如果在(a,b)上(g^{'}left( x ight) eq 0),那么有
为什么说该定理是更广义的微分中值定理呢?微分中值定理就是上面这个等式中令g(x)=x的情形[5]。至于广义微分中值定理的证明,我们只用令(hleft( x ight) = leftlbrack fleft( b ight) - fleft( a ight) ight brack gleft( x ight) - leftlbrack gleft( b ight) - gleft( a ight) ight brack fleft( x ight)),然后对其应用微分中值定理便不难得证。
下一节我会讲到洛必达法则(L’Hospital’s rule),我将向各位提供可以理解掌握的、能从中吸取到有用经验的∞/∞型洛必达法则的证明方法,敬请期待!
Joel R. Hass, Christopher E. Heil, Maurice D. Weir ,Thomas’ calculus, 14^th^ edition, p191 ↩︎
Joel R. Hass, Christopher E. Heil, Maurice D. Weir ,Thomas’ calculus, 14^th^ edition, p193 ↩︎
Morris Kline, Calculus : an intuitive and physical approach, second edition, Chapter 13,Section 2 ↩︎
Stephen Abbott, Understanding Analysis, second edition, p158 ↩︎
常庆哲、史济怀,《数学分析教程》上册(2003),p155 ↩︎