Description
Sylvia 是一个热爱学习的女孩子。
前段时间,Sylvia 参加了学校的军训。众所周知,军训的时候需要站方阵。
Sylvia 所在的方阵中有 n×m 名学生,方阵的行数为 n,列数为 m。
为了便于管理,教官在训练开始时,按照从前到后,从左到右的顺序给方阵中的学生从 1 到 n×m 编上了号码(参见后面的样例)。即:初始时,第 i 行第 j 列的学生的编号是 (i−1)×m+j。
然而在练习方阵的时候,经常会有学生因为各种各样的事情需要离队。在一天中,一共发生了 q 件这样的离队事件。每一次离队事件可以用数对 (x,y) (1≤x≤n,1≤y≤m) 描述,表示第 x 行第 y 列的学生离队。
在有学生离队后,队伍中出现了一个空位。为了队伍的整齐,教官会依次下达这样的两条指令:
向左看齐。这时第一列保持不动,所有学生向左填补空缺。不难发现在这条指令之后,空位在第 x 行第 m 列。
向前看齐。这时第一行保持不动,所有学生向前填补空缺。不难发现在这条指令之后,空位在第 n 行第 m 列。
教官规定不能有两个或更多学生同时离队。即在前一个离队的学生归队之后,下一个学生才能离队。因此在每一个离队的学生要归队时,队伍中有且仅有第 n 行第 m 列一个空位,这时这个学生会自然地填补到这个位置。
因为站方阵真的很无聊,所以 Sylvia 想要计算每一次离队事件中,离队的同学的编号是多少。
注意:每一个同学的编号不会随着离队事件的发生而改变,在发生离队事件后方阵中同学的编号可能是乱序的。
Input
输入共 q+1 行。 第 1 行包含 3 个用空格分隔的正整数 n,m,q 表示方阵大小是 n 行 m 列,一共发生了 q 次事件。
接下来 q 行按照事件发生顺序描述了 q 件事件。每一行是两个整数 x,y 用一个空格分隔,表示这个离队事件中离队的学生当时排在第 x 行第 y 列。
Output
按照事件输入的顺序,每一个事件输出一行一个整数,表示这个离队事件中离队学生的编号。
Sample Input
2 2 3
1 1
2 2
1 2
Sample Output
1
1
4
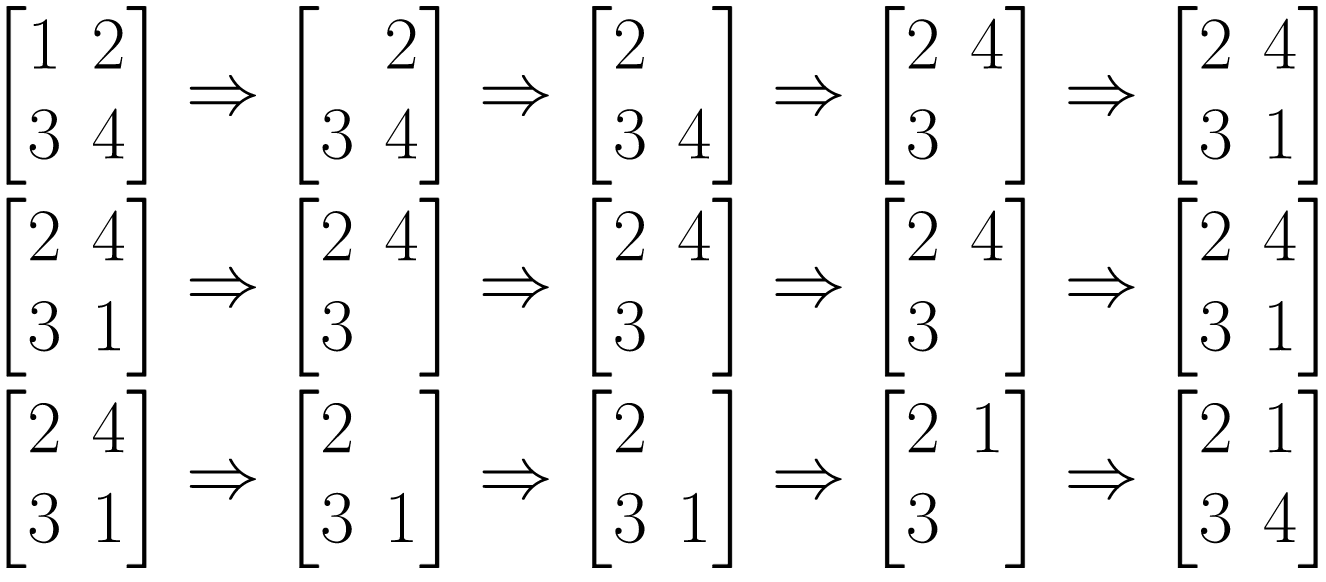
列队的过程如上图所示,每一行描述了一个事件。
在第一个事件中,编号为 1 的同学离队,这时空位在第一行第一列。接着所有同学 向左标齐,这时编号为 2 的同学向左移动一步,空位移动到第一行第二列。然后所有同 学向上标齐,这时编号为 4 的同学向上一步,这时空位移动到第二行第二列。最后编号 为 1 的同学返回填补到空位中。
Hint
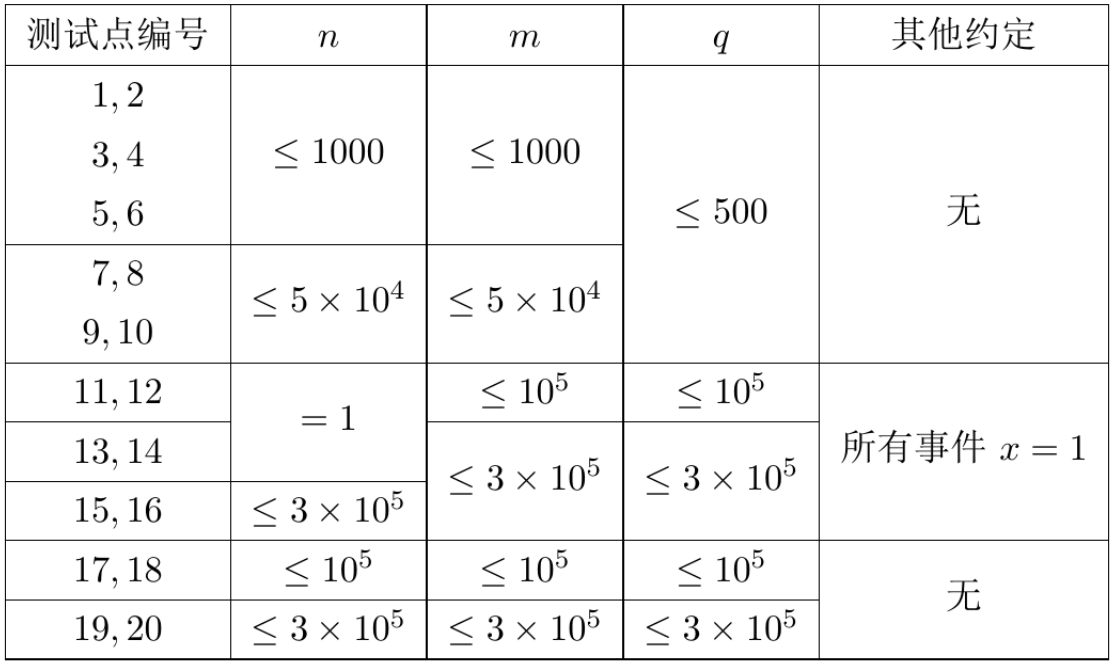
数据保证每一个事件满足 1≤x≤n,1≤y≤m。
分析
这道题有很多解法,树状数组啊,平衡树啊啥的,但是我这个人天生愚钝,树状数组想不出,平衡树调不对,所以...
我们先观察每取出来一个数,相当于是在 从这个数开始,到这一行末尾,在向下拐到最下面的一个“7”形数列 中,把这个数提出来放到最后,显然x=1就可以用一个平衡树解决。
如果没有x==1的限制呢?打个比方,在下图中,提出#,放到@处。最后一列少了x,多了#,其余顺序不变。那我们就可以用一个数据结构单独维护最后一列。而除掉最后一列的数,#所在行多了一个x,那我们对于每一行前m-1一个数都用一个数据结构维护即可。
我们对于询问#并删除的操作分为一下三部:
1.在#所在行X的里查询第Y的数字ans,删除
2.在最后一列末尾的加入ans
3.如果#不在最后一列,在最后一列查询第X的数字,删除,并加到#所在行X的末尾
这样的Splay是存不下的,
我们想到动态开点线段树,每加入一个数往右边拓宽即可。
。。。。。。
。# 。。。x
。。。。。。
。。。。。@
Code

1 #include<set> 2 #include<map> 3 #include<queue> 4 #include<stack> 5 #include<cmath> 6 #include<cstdio> 7 #include<cstring> 8 #include<iostream> 9 #include<algorithm> 10 #define RG register ll 11 #define rep(i,a,b) for(RG i=a;i<=b;++i) 12 #define per(i,a,b) for(RG i=a;i>=b;--i) 13 #define ll long long 14 #define inf (1<<29) 15 #define maxn 300005 16 #define maxm 10000005 17 using namespace std; 18 ll X,Y; 19 ll n,m,Q,tn,id; 20 ll ls[maxm],rs[maxm],sz[maxm],rt[maxm],val[maxm],tail[maxn]; 21 inline ll read() 22 { 23 ll x=0,f=1;char c=getchar(); 24 while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();} 25 while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();} 26 return x*f; 27 } 28 29 inline ll qlen(ll l,ll r) 30 { 31 if(tn>n) 32 { 33 if(r<=n) return r-l+1ll; 34 if(l<=n) return n-l+1ll; 35 return 0; 36 } 37 if(r<m) return r-l+1ll; 38 if(l<m) return m-l; 39 return 0; 40 } 41 42 ll query(ll &pos,ll l,ll r,ll aim) 43 { 44 if(!pos) 45 { 46 pos=++id; 47 sz[pos]=qlen(l,r); 48 if(l==r) 49 { 50 if(tn>n) val[pos]=l*m; 51 else val[pos]=(tn-1ll)*m+l; 52 } 53 } 54 sz[pos]--; 55 if(l==r) return val[pos]; 56 ll mid=(l+r)>>1ll; 57 if( (!ls[pos]&&aim<=(mid-l+1ll)) || aim<=sz[ls[pos]] ) return query(ls[pos],l,mid,aim); 58 else if(ls[pos]) return query(rs[pos],mid+1ll,r,aim-sz[ls[pos]]); 59 else return query(rs[pos],mid+1ll,r,aim-(mid-l+1ll)); 60 } 61 62 void update(ll &pos,ll l,ll r,ll aim,ll num) 63 { 64 if(!pos) 65 { 66 pos=++id; 67 sz[pos]=qlen(l,r); 68 if(l==r) val[pos]=num; 69 } 70 sz[pos]++; 71 if(l==r) return; 72 ll mid=(l+r)>>1ll; 73 if(aim<=mid) update(ls[pos],l,mid,aim,num); 74 else update(rs[pos],mid+1ll,r,aim,num); 75 } 76 77 int main() 78 { 79 RG ans,lim; 80 n=read(),m=read(),Q=read();lim=max(n,m)+Q+1; 81 rep(i,1,n) tail[i]=m-1;tail[n+1]=n; 82 while(Q--) 83 { 84 X=read(),Y=read(); 85 86 //First opt:Query and delete 87 if(Y==m) ans=query(rt[tn=n+1],1,lim,X); 88 else ans=query(rt[tn=X],1,lim,Y); 89 printf("%lld ",ans); 90 91 //Second opt:Add to the last tree 92 update(rt[tn=n+1],1,lim,++tail[n+1],ans); 93 94 //Third opt:Change the numb of last position of query line 95 if(Y==m) continue; 96 ans=query(rt[tn=n+1],1,lim,X); 97 update(rt[tn=X],1,lim,++tail[X],ans); 98 } 99 return 0; 100 }
