Hausdorff Distance(豪斯多夫距离)
参考博客:
http://cgm.cs.mcgill.ca/~godfried/teaching/cg-projects/98/normand/main.html
理解:
Hausdorff距离是描述两组点集之间相似程度的一种量度,它是两个点集之间距离的一种定义形式。
假设有两组集合A={a1,…,ap},B={b1,…,bq},则这两个点集合之间的Hausdorff距离定义为
H(A,B)=max(h(A,B),h(B,A)) (1)
其中,
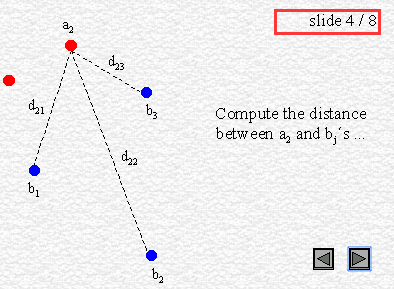
h(A,B)=max(a∈A)min(b∈B)‖a-b‖ (2)
h(B,A)=max(b∈B)min(a∈A)‖b-a‖ (3)
‖·‖是点集A和B点集间的距离范式(如:L2或Euclidean距离).
这里,式(1)称为双向Hausdorff距离,是Hausdorff距离的最基本形式;式(2)中的h(A,B)和h(B,A)分别称为从A集合到B集合和从B集合到A集合的单向Hausdorff距离.即h(A,B)实际上首先对点集A中的每个点ai到距离此点ai最近的B集合中点bj之间的距离‖ai-bj‖进行排序,然后取该距离中的最大值作为h(A,B)的值.h(B,A)同理可得.
由式(1)知,双向Hausdorff距离H(A,B)是单向距离h(A,B)和h(B,A)两者中的较大者,它度量了两个点集间的最大不匹配程度.
以下是参考文献的摘录:
1.Introduction
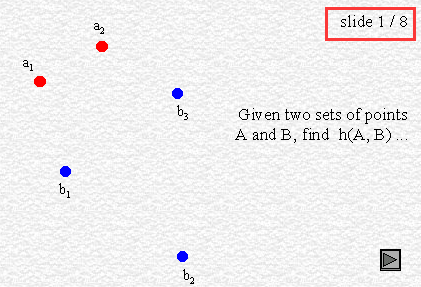
When talking about distances, we usually mean the shortest : for instance, if a point X is said to be at distance D of a polygon P, we generally assume that D is the distance from X to the nearest point of P..
The same logic applies for polygons : if two polygons A and B are at some distance from each other, we commonly understand that distance as the shortest one between any point of A and any point of B.
Formally, this is called a minimin function, because the distance D between A and B is given by :
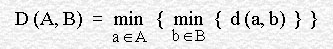
即 A集合中的任一点ai 到集合B中的任意点的最短的距离di,然后在这些距离di中选择距离最短的,即作为两个集合A与B的距离。
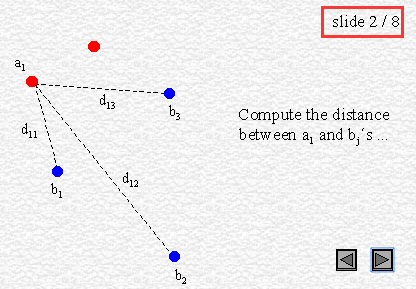
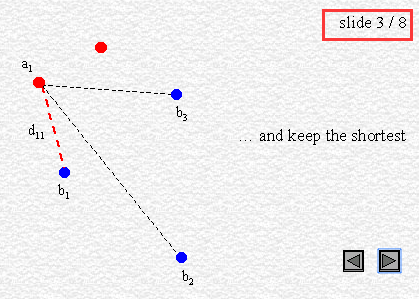
That definition of distance between polygons can become quite unsatisfactory for some applications (并不适用于描述两个多边形的位置关系); let's see for example fig. 1. We could say the triangles are close to each other considering their shortest distance, shown by their red vertices. However, we would naturally expect that a small distance between these polygons means that no point of one polygon is far from the other polygon. In this sense, the two polygons shown in fig. 1 are not so close, as their furthest points, shown in blue, could actually be very far away from the other polygon. Clearly, the shortest distance is totally independent of each polygonal shape.

另一个例子:
Another example is given by fig. 2, where we have the same two triangles at the same shortest distance than in fig. 1, but in different position. It's quite obvious that the shortest distance concept carries very low informative content, as the distance value did not change from the previous case, while something did change with the objects.
两个多边形的最短距离提供的信息很少。 如下图,与图1同样最短距离的两个多边形的位置却不同。

因此:
定义Hausdoff Distance 距离可以捕捉两个多边形的细微之处, 因此要忽略其最短距离。
2. Hausdoff Distance 定义
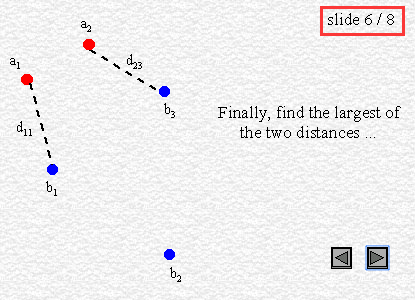
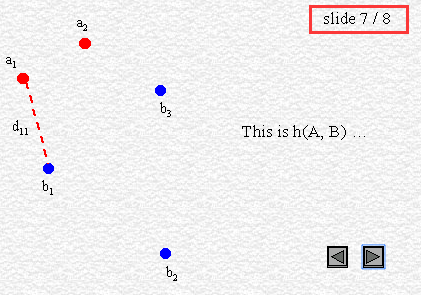
More formally, Hausdorff distance from set A to set B is a maximin function, defined as

where a and b are points of sets A and B respectively, and d(a, b) is any metric between these points ; for simplicity, we'll take d(a, b) as the Euclidian distance between a and b. If for instance A and B are two sets of points, a brute force algorithm would be :
即: 即 A集合中的任一点ai 到集合B中的任意点的最短的距离di,然后在这些距离di中选择距离最长(远)的,即作为两个集合A与B之间的Hausdoff Distance。
Brute force algorithm : 1. h = 0 2. for every point ai of A, 2.1 shortest = Inf ; 2.2 for every point bj of B dij = d (ai , bj ) if dij < shortest then shortest = dij 2.3 if shortest > h then // 记录每个ai 到B中的所有点中最小的 h = shortest

算法的时间复杂度是:O(nm)
·This algorithm obviously runs in O(n m) time, with n and m the number of points in each set.
注意:
(1)Hausdoff Distance 是非对称的, 即单向的。是由方向的。h(A,B) 称为forward Hausdoff Distance, h(B, A)称为Backward Hausdoff Distance。
(2)如果A, B是多边形,而不是离散的点集, Hausdoff Distance同样适用。 即H(A, B)适应于所有多边形,线段定义的点集。
(3)Hausdoff Distance给出了两个多边形相互接近的程度, 即,一个多边形(点集)到另一个多边形(点集)最大距离。这与最短距离的定义不同,因为其仅适用于每个多边形的一个点,而不考虑多边形的所有其他点。
(4)直观的理解就是:Hausdoff Distance 对两个多边形的位置距离敏感,而不敏感于多边形位置之间的最短距离。
如下图: 两个多边形制件的Hausdoff Distance 是截然不同的。
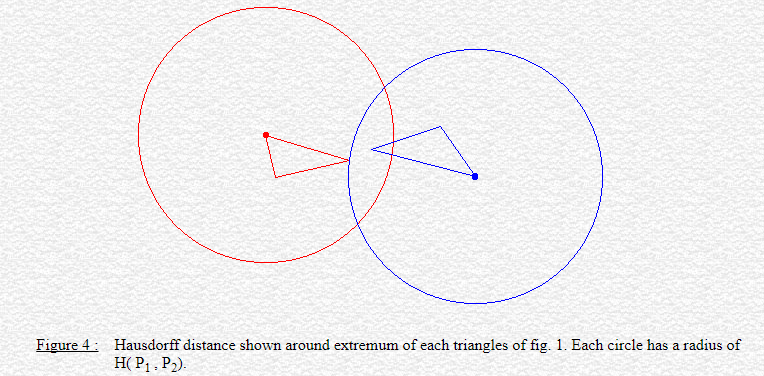

3. Hausdoff Distance的计算
假定:
(1)假定两个多边形是简单的凸多边形;
(2)两个多边形制件不相接处,即相交,也不互相包含。
基础概念:
(1)单调链: 链条C(连续的边)如果是在D方向上是单调的, 则与D方向正交的直线L 与C的交点只有一个,则说明C在D向是单调的。

直线L通过多边形P中的某个点, 如果多边形P的内部区域完全在L的一侧, 则该L是一条支撑线
注意: 支撑线L是切片的泛化形式。

引理:
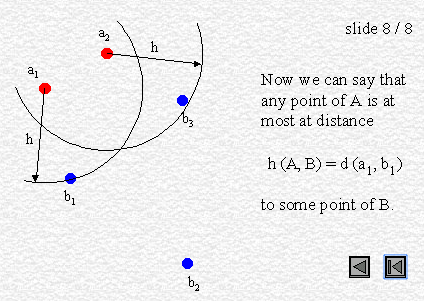
we assume two points a and b that belong respectively to polygons A and B, such that :
d (a, b) = h (A, B)
即: a是多边形A(点集)中距离多边形B最远的点。 而b是多边形B(点集)中距离多边形A最近的点。
引理(1.1)The perpendicular to ab at a is a supporting line of A, and A is on the same side as B relative to that line.
垂直于两个点a,b且在定a位置的多边形A的支撑线,则相对于该支撑线,则B也在同侧。
因为:从Hausdoff Distance定义中,则点a 出的直线必然是多边形A的“支撑线” ,且,As illustrated below, if a is the furthest point of A relative to b, then a circle C centered at b and of radius ab will completely enclose A. Because C contains all points of A, then its tangent to a is a supporting line of A.

引理(1.2):The perpendicular to ab at b is a supporting line of B, and a and B are on different sides relative to that line
垂直于ab 且位于b点的垂线是B多边形的支撑线。 且 a 和B在该线的不同侧。
证明:If b is the closest point of B from a, then a circle C of radius abcentered at a contains only one point of B, namely b. The tangent to C is thus a supporting line of B.
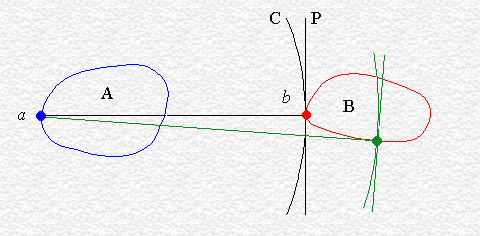
引理(2)There is a vertex x of A such that the distance from x to B is equal to h (A, B).
A 中存在一点x,且x 到B的距离与 h(A,B)相等。
证明:a line going from a vertex b of a triangle abc to some point that belongs to the opposite side ß is always shorter than one of ab or cb, or both.

引理(3)
4. 算法:
因为引理2,则没有必要计算出开始多边形的每一个点, 仅仅计算多边形的“顶点”即可。
情况一:
注意: 算法最近点只能是目标多边形的顶点,或者是垂直于目标多边形某条边的垂点z。因此,要检查是否存在最近的点。
Function z = CheckForClosePoint (a, b1 , b2 ) :
Compute the position z where the line that passes through b1 and b2 crosses its perpendicular through a ;
计算垂直于穿过b1,b2的直线,且经过点a的位置c。
过程: 如果z是b1,b2中间的点,则返回z, 否则再计算b2点处的直线P(出至于直线a,b2)是否是多边形B的“支撑线”,如果是,则返回b2,否则返回Null。
if z is between b1 b2 then return z ; else compute at b2 a line P perpendicular to the line ab2 ; if P is a supporting line of B then return b2 ; else return NULL.
主程序:
开始计算主程序,
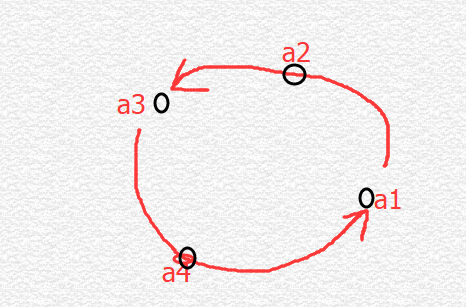
注意:所有多边形的顶点序列都是通过“逆时针”的顺序列出。
Algorithm for computing h(A, B) :
(枚举ai 到B中的最近距离di) 1. From a1, find the closest point b1 and compute d1 = d ( a1, b1 ) 2. h(A, B) = d1 3. for each vertex ai of A,
(因为是逆时针依次遍历A中的点集序列,而bi则根据ai+1情况进行相应移动) 3.1 if ai+1 is to the left of aibi find bi+1 , scanning B counterclockwise with CheckForClosePoint from bi if ai+1 is to the right of aibi find bi+1 , scanning B clockwise with CheckForClosePoint from bi if ai+1 is anywhere on aibi bi+1 = bi
(更新当前距离di+1) 3.2 Compute di+1 = d (ai+1 , bi+1 )
(始终取值为每次更新的最大值) 3.3 h (A, B) = max { h (A, B), di+1 }
因为:多边形是简单凸多边形,且逆时针,在遍历的时候ai, ai+1 必然会发生“转向”,这个过程有三种情况
(1)ai+1 在 aibi 直线的左边, 则遍历ai+1趋势继续“单调”, 因为为了找到最近的点, 则要【逆时针移动】B中当前点bi的下一个点bi+1 的距离判断(check)此点bi+1;
(2)ai+1 在 aibi 直线上, 则遍历ai+1即将不在“单调”,此刻必然ai +1 到bi的距离发生变化,为了找到最近的点,则此时将bi+1 视为bi,需要重新更新距离;
(3)ai+1 在 aibi 直线的右边, 与情况(1)相反, 则,为了找到最近的点,需要【顺时针移动】B中的bi的下一个bi+1点,然后cheke此点bi+1”
5. 复杂度分析
If polygons A and B respectively have n and m vertices, then :
- Step 1 can clearly be done in O(m) time ;
- Step 2 takes constant time O(1) ;
- Step 3 will be executed (n-1) times, that is O(n) ;
- Step 3.1 will not be executed in total more than O(2m). This is a consequence of lemma 3, which guarantees that polygon B can not be scanned more than twice ;
- Steps 3.2 and 3.3 are done in constant time O(1) ;
So the algorithm for computing h(A, B) takes :
O(m) + O(n) + O(2m) = O(n+m)
To find H(A, B), the algorithm needs to executed twice ; the total complexity for computing Hausdorff distance then stays linear to O(n+m).
6. 案例分析
Hausdorff distance 应用是图像匹配,如图像分析,机器人的视觉导航,电脑辅助手术,
Basically, the Hausdorff metric will serve to check if a template image is present in a test image ; the lower the distance value, the best the match.That method gives interesting results, even in presence of noise or occlusion (when the target is partially hidden).

We want to find if the small image is present, and where, in the large image. The first step is to extract the edges of both images, so to work with binary sets of points, lines or polygons :
Edge extraction is usually done with one of the many edge detectors known in image processing, such as Canny edge detector, Laplacian, Sobel, etc. After applyingRucklidge's algorithm that minimizes Hausdorff distance between two images, the computer found a best match :


For this example, at least 50 % of the template points had to lie within 1 pixel of a test image point, and vice versa. Some scaling and skew were also allowed, to prevent rejection due to a different viewing angle of the template in the test image (these images and results come from Michael Leventon's pages). Other algorithms might allow more complicated geometric transformations for registering the template on the test image.
an online demo is definitely beyond the scope of this Web project ! So here are some Web resources about image matching with Hausdorff distance :
- Hausdorff-based image comparison
A vision project that uses the generalized Hausdorff distance
to locate a template image in an indoor scene. - Hausdorff distance for object tracking and classification
Hausdorff distance used with a multi-layer perceptron
for recognizing and tracking cars in a road scene. - Computer-vision-enabled ophthalmic augmented reality environment
An interesting application of Hausdorff distance for merging
partially overlapping images into a single image. - Comparing 2D images of the 3D world
Conference material by Daniel Huttenlocher on object recognition.
Briefly introduces some problems of image analysis, and compares
the generalized Hausdorff distance with more traditional methods.
endl;