1. 引言
降维是对数据高维度特征的一种预处理方法。降维是将高纬度的数据保留下最重要的一些特征,去除噪声和不重要的特征,从而实现提升数据处理速度的目的。在实际的生产和应用中,降维在一定的信息损失范围内,可以节省大量的时间和成本。
PCA(principal compount analysis),即主成分分析法,是一种使用最广泛的数据压缩算法。在PCA中,数据从原来的坐标系转换到新的坐标系,由数据本身决定。转换坐标系时,以方差最大的方向作为坐标轴方向,因为数据的最大方差给出了数据的最重要的信息。第一个新坐标轴选择的是原始数据中方差最大的方法,第二个新坐标轴选择的是与第一个新坐标轴正交且方差次大的方向。重复该过程,重复次数为原始数据的特征维数。
通过这种方式获得的新的坐标系,我们发现,大部分方差都包含在前面几个坐标轴中,后面的坐标轴所含的方差几乎为0,。于是,我们可以忽略余下的坐标轴,只保留前面的几个含有绝不部分方差的坐标轴。事实上,这样也就相当于只保留包含绝大部分方差的维度特征,而忽略包含方差几乎为0的特征维度,也就实现了对数据特征的降维处理。
那么,我们如何得到这些包含最大差异性的主成分方向呢?事实上,通过计算数据矩阵的协方差矩阵,然后得到协方差矩阵的特征值及特征向量,选择特征值最大(也即包含方差最大)的N个特征所对应的特征向量组成的矩阵,我们就可以将数据矩阵转换到新的空间当中,实现数据特征的降维(N维)。
既然,说到了协方差矩阵,那么这里就简单说一下方差和协方差之间的关系,首先看一下均值,方差和协方差的计算公式:
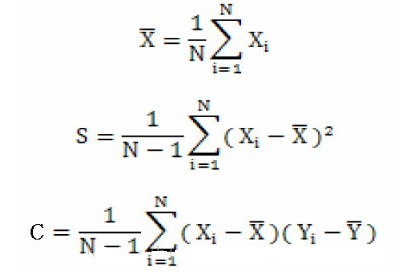
方差的计算公式,我们知道方差的计算是针对一维特征,即针对同一特征不同样本的取值来进行计算得到;而协方差则必须要求至少满足二维特征。可以说方差就是协方差的特殊情况。
2. 优点
使得数据集更容易使用;
降低算法的计算开销;
降低噪声;
使得结果更容易理解;
3. PCA算法实现
去除平均值
计算协方差矩阵
计算协方差矩阵的特征值和特征向量
将特征值排序
保留前N个最大的特征值对应的特征向量
将数据转换到上面得到的N个特征向量构建的新空间中(实现了特征压缩)
上述降维过程,首先根据数据矩阵的协方差的特征值和特征向量,得到最大的N个特征值对应的特征向量组成的矩阵,可以称之为压缩矩阵;得到了压缩矩阵之后,将去均值的数据矩阵乘以压缩矩阵,就实现了将原始数据特征转化为新的空间特征,进而使数据特征得到了压缩处理。当然,也可以根据压缩矩阵和特征均值,反构得到原始数据矩阵,通过这样的方式可以用于调试和验证。