这一次,我来学习如何解决一个著名的问题:汉诺塔问题
总所周知,汉诺塔问题的主要提干是:
汉诺塔(又称河内塔)问题是源于印度一个古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定,在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘。
根据题意,我们下意识会觉得这个题目实际上很难,因为它加上了一些限定条件:三根柱子间一次只能移动一个原盘,自始至终大圆盘不能在小圆盘上等等……
我们最终的任务是把最左边的柱子上的圆盘移动到最右边去,这显然需要一个递归的函数去实现……
单纯地,我们通过算法可以将一个汉诺塔的解决方案编写出来:
def move(n,a,b,c):
if n==1: #当只有一个圆盘时只需从最左端移向最右端
print(a,'-->',c) #面板可视化,可以通过列举图标表现移动的步骤形式
else:
move(n-1,a,c,b) #将前n-1个盘子从a移动到b上
move(1,a,b,c) #将最底下的最后一个盘子从a移动到c上
move(n-1,b,a,c) #将b上的n-1个盘子移动到c上
move(3,'A','B','C')
效果:
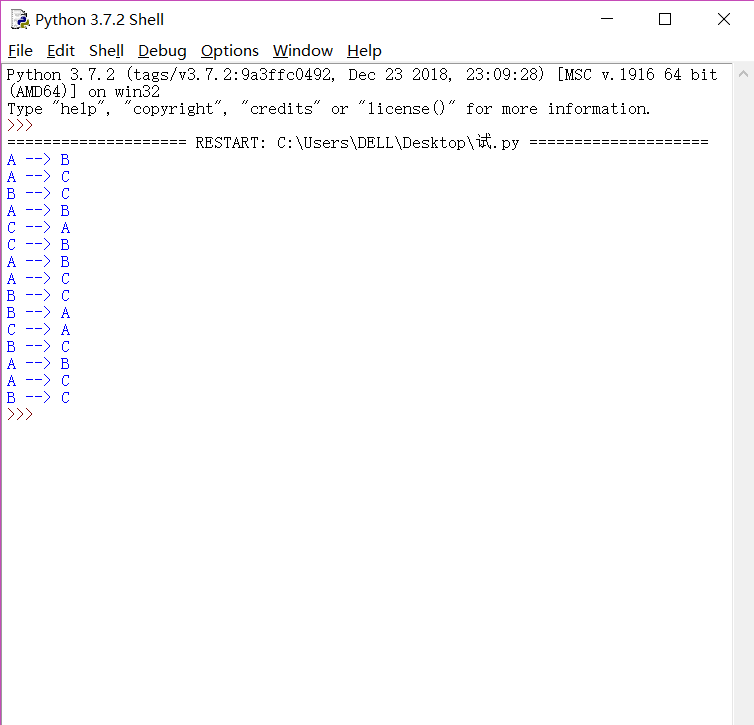
Wow!就是这么简单,两三行的代码就可以解决这个问题,这就是代码之美,仔细看这几行代码,原来我们只是将我们希望的移动结果以及移动规则告诉计算机,就可以解决这个“我们认为好像很难的题目”!
那么,我们解决了算法的部分,那要如何将它像现实中那样可视化表现出来呢?
我们想到了turtle库!啊~好亲切啊~
没错!就是用turtle库将我们的各种元素“柱子”,“盘子”给画出来!,这当然不是什么难事,最重要的是如何将它们的移动与代码合成起来,用上述代码指导它们的移动(move)?
emmmmm……好吧,也许还是因为我的能力比较有限,目前比较难以实现!
通过网上找了一些解决的方法资料,结合自己所学,我通过数据结构中的“栈”的概念,结合turtle库
我们写下了以下代码:
import turtle
class Stack: #宏观定义算法用法
def __init__(self):
self.items = []
def isEmpty(self):
return len(self.items) == 0
def push(self, item):
self.items.append(item)
def pop(self):
return self.items.pop()
def peek(self):
if not self.isEmpty():
return self.items[len(self.items) - 1]
def size(self):
return len(self.items)
def drawpole_3(): #画出汉诺塔的poles
t = turtle.Turtle()
t.hideturtle()
def drawpole_1(k):
t.up()
t.pensize(10)
t.pencolor('blue')
t.speed(100)
t.goto(200*(k-1), 100)
t.down()
t.goto(200*(k-1), -100)
t.goto(200*(k-1)-20, -100)
t.goto(200*(k-1)+20, -100)
drawpole_1(0)#画出汉诺塔的poles[0]
drawpole_1(1)#画出汉诺塔的poles[1]
drawpole_1(2)#画出汉诺塔的poles[2]
def creat_plates(n) :#制造n个盘子
plates=[turtle.Turtle() for i in range(n)]
for i in range(n):
plates[i].up()
plates[i].hideturtle()
plates[i].shape("square")
plates[i].shapesize(1,8-i)
plates[i].goto(-200,-90+20*i)
plates[i].showturtle()
return plates
def pole_stack(): #制造poles的栈(由于每次只能移动一个盘子且盘子只能从最上面开始拿,故用栈)
poles=[Stack() for i in range(3)]
return poles
def moveDisk(plates,poles,fp,tp):#把poles[fp]顶端的盘子plates[mov]从poles[fp]移到poles[tp](其实就是上述的第一个的最基本的那个算法)
mov=poles[fp].peek()
plates[mov].goto((fp-1)*200,150)
plates[mov].goto((tp-1)*200,150)
l=poles[tp].size() #确定移动到底部的高度(恰好放在原来最上面的盘子上面)
plates[mov].goto((tp-1)*200,-90+20*l)
def moveTower(plates,poles,height,fromPole, toPole, withPole):#递归放盘子
if height >= 1:
moveTower(plates,poles,height-1,fromPole,withPole,toPole)
moveDisk(plates,poles,fromPole,toPole)
poles[toPole].push(poles[fromPole].pop())
moveTower(plates,poles,height-1,withPole,toPole,fromPole)
myscreen=turtle.Screen()
drawpole_3()
n=int(input("请输入汉诺塔的层数并回车:
"))
plates=creat_plates(n)
poles=pole_stack()
for i in range(n):
poles[0].push(i)
moveTower(plates,poles,n,0,2,1)
myscreen.exitonclick()
此时我们输入盘子的数量:
于是乎,回车键以后我们就可以得出下面的动画啦~
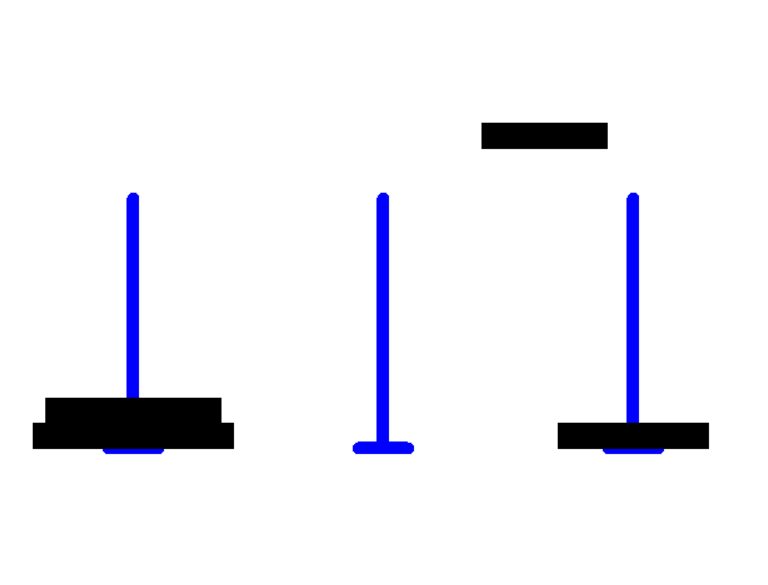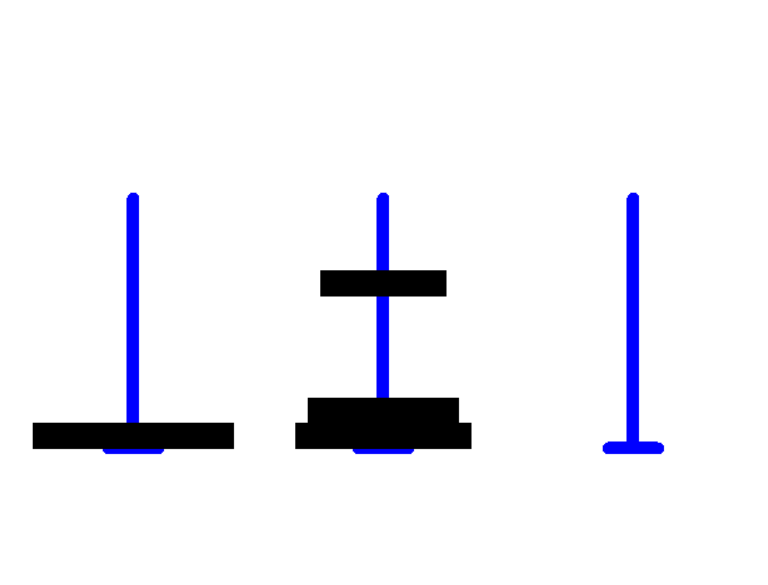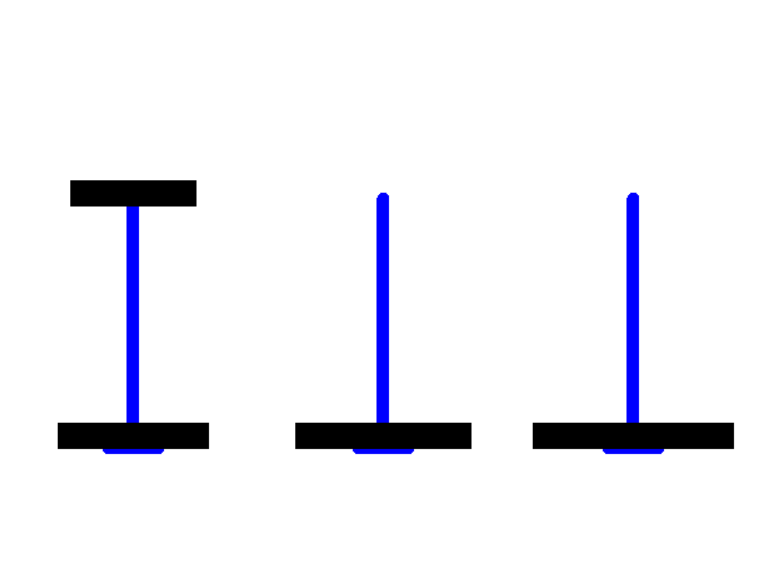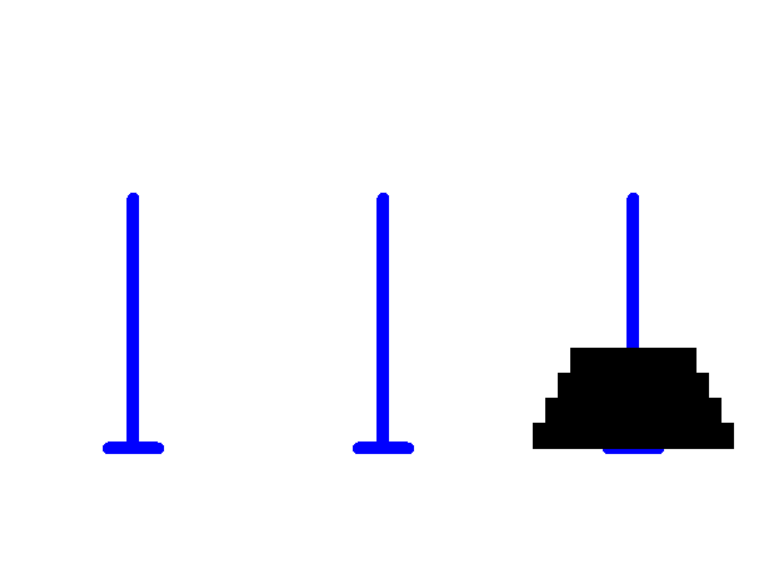
cool!
通过封装多个不同功能的python代码,结合多个方法就可以实现这样看似复杂的实现!
python真是越来越有趣了~