转载自:https://www.cnblogs.com/visionsl/p/9075756.html
本文重点?
- 用SHA256算法得到哈希值
- 挖矿起什么作用
- 块是怎么连接成链的
基本要素:哈希算法
哈希看起来就像是一串64位的随机的16进制的字符串, 本质上是某些数字数据的一个指纹; 也就是说每个不同的(文本)内容都有对应不同的指纹(哈希值)
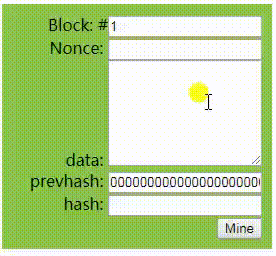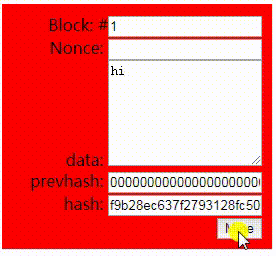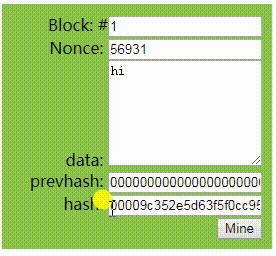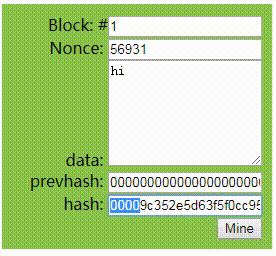
先来看看下图中的演示, 我们在data区内输入任意内容, 下面的hash区内就会自动实时计算与之对应的Hash值;并且data区的内容不管是只有1个字符, 还是你把整个图书馆的内容都录进去, hash得到的永远是一串64个字符的哈希值, 同时你永远也不可能事先猜得到你输入的内容将得到什么样的哈希值
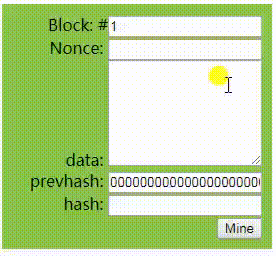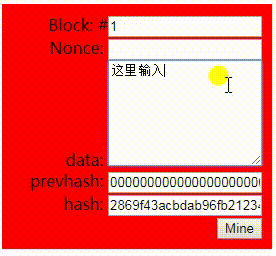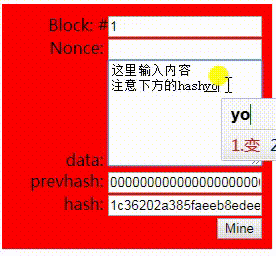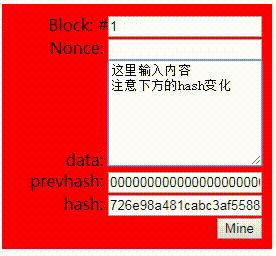
利用这个特性, 我们就可以针对你要保护的内容进行哈希并保存下来,
在此基础上, 我们把它拓展成称为BLOCK的东西, 它至少包含
Block - 在本例中它只是个序号,每个块都有不一样的序号 Nonce - 随机数, 后面会讲到 Data - 内容区
常见的做法是先把这几个数据加起来, 可以理解为区块头: 区块序号+Nonce(随机值)+data(需保护的内容区)
即使正式应用中会有更多的数据, 比如要加上密钥和时间戳, 但基本原理是相通的
然后把这些内容进行SHA256运算加密, 得到一串64位的哈希值, 如果内容被篡改,那么这串哈希值必然会变化
明白了哈希值如何产生, 接下来看下一步: 挖矿
必要的步骤:也来挖个矿
仔细且耐心观察下图, 在点击了[Mine]按钮后,经过较长时间的运算,得到了4个0开头的哈希值
这是个相对罕见的散列(哈希)值, 我们可以认定它就是这个区块的指纹, 如果这时你尝试去修改data区内容, 会发现hash值发生变化, 并且不再是4个0开头, 证明这个区块被篡改过了
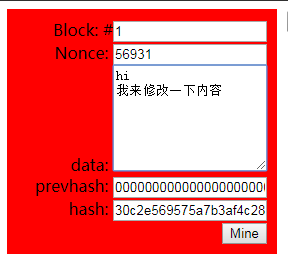
像下图, 如果内容被修改, 哈希变成了不是4个0开头, 并且背景变成了红色, 你就可以知道这个块的内容不再是有效的或签过名的, 它已经被篡改过,不安全的了.
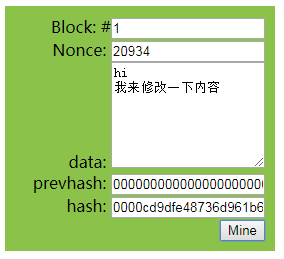
这时重新Mine一下, 等待一段时间后,重新得到4个0开头的哈希值;
要注意的是Nonce变化了! 这是Nonce在这里出现的原因!!
不同的内容, 需要匹配不同的Nonce才能得到4个0开头的哈希值, Mine的过程其实就是算法在寻找合适的随机数搭配内容以使得再次得到4个0开头的哈希值,
在寻找Nonce的过程, 就叫挖矿!
现在明白为什么要挖矿了, 接下来把上面的知识串起来, 形成链
生成区块,链接成最简单的区块链
对每个区块头进行SHA256加密哈希,可生成一个哈希值。通过这个哈希值,可以识别出区块链中的对应区块。同时,每一个区块都可以通过其区块头的“父区块哈希值”字段引用前一区块(父区块)。也就是说,每个区块头都包含它的父区块哈希值。这样把每个区块链接到各自父区块的哈希值序列就创建了一条一直可以追溯到第一个区块(创世区块)的链条。
看下图是个由4个块组成的链, 每个块都有负责记住上个块的prevhash, 以及自己的hash, 一个串一个, 就形成了链
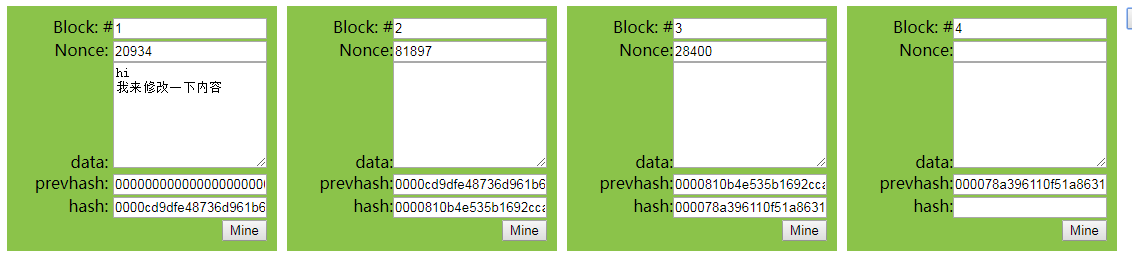
在这个链条上, 如果中间的块被恶意修改了数据,会发生什么?
在下图的演示中可以看到, 如果第2个区块被恶意修改数据的话, 从第2个块起就会因哈希值(指纹)变化导致它和后面的哈希值全部出问题, 安全校验会检测出有区块出问题!

扩展阅读
接下来怎么解决这个问题呢?
就会涉及到分布式存储的问题, 要把这个链条(数据)存放到各个终端去-----去中心化!
并加入投票机制, 当有链条的数据出问题时, 用多数正确的链接替换掉出问题的链条, 以保存数据的正确性
这也是我们常说的除非你能黑掉51%的数据(链条), 才能真正篡改掉数据的真正原因所在!
上文只是简单讲了一下区块链的一些基本运作原理, 真想掌握的还要深入学习
但对于只想知道区块链是怎么回事的朋友, 应该足够了