在计算机科学中,树由称为结点的元素按照层次结构的方式组织而成。层次结构最顶端的结点称为根。与根结点直接相连的结点称为根的子结点,通常子结点本身也有属于它们自己的子结点。除了根结点外,在这个层次体系中的每个结点都有唯一的父结点,也就是与其直接相连的上级结点。
一个节点拥有多少个子节点取决于树的类型,这个量值称为树的的分支因子,它决定了当插入结点时树的分支扩展的速度。
二叉树是一种相对简单但功能强大的树,其树的分支因子值为2。
二叉树的介绍
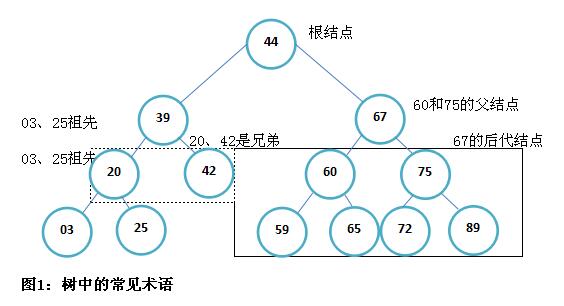
二叉树是一种将结点按照层次结构组织起来的数据结构,每个结点最多只有两个与它直接相关联的子结点。直接连接在结点下方的那个结点称为子结点,而与每个子结点直接相连的上方结点称为父结点。结点也有兄弟、子孙和祖先。一个结点的兄弟结点是它的父亲结点的其他子结点。一个结点的子孙结点是其所有分支下的结点。而结点的祖先结点则是在该结点与根结点之间路径上的所有结点。
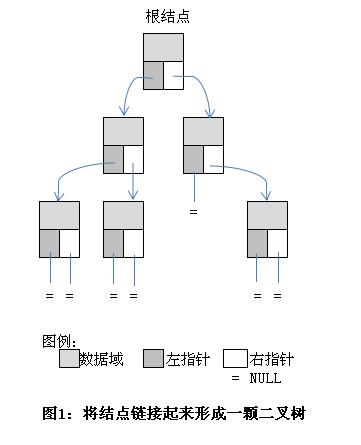
二叉树中的每一个结点都包含3部分:一个数据成员和左右两个指针。
通过这种3个成员的结构体,将每个结点的左右指针分别指向该结点的子结点,以此来构建一棵二叉树。如果某个结点没有对应的左子结点或右子结点,就将相应的指针设置为NULL。这种方法便于标识出一个分支的结束。
树的分支是一系列的结点,从根结点开始到某个叶子结点结束。
叶子结点位于树的边缘,且没有子结点。多颗树组成的集合称为森林。
树的4种周游算法
1、先序遍历
给定一颗树,按照先序遍历的方式,首先访问它的根结点,然后是左子结点,最后是右子结点。按照从左到右的方式依次遍历各个结点,以相同的方式将左子结点和右子结点当做新的子树的根。
先序遍历是按照深度优先的方式遍历结点的。
2、中序遍历
给定一颗树,按照中序遍历的方式,首先访问左子结点,然后是根结点,最后是右子结点。按照从左到右的顺序依次访问各个结点,以相同的方式将左子结点和右子结点当做新的子树的根。
3、后序遍历
给定一颗树,按照后序遍历的方式,首先访问左子结点,然后是右子结点,最后是根结点。按照从左到右的顺序依次访问各个结点,以相同的方式将左子结点和右子结点当做新的子树的根。
4、层级遍历
要用层级遍历周游一颗树,首先访问树的根,然后依次向下层处理,按照从左到右的顺序访问每层的结点。层级遍历运用了广度优先的策略。

树的平衡
对于给定数量的结点,保证树的高度尽可能的短的过程叫做树的平衡。这意味着,在结点加入下一层之前必须保证本层结点满额。正式的说法是,如果满足树的所有叶子节点都在同一层上,或者所有叶子结点都在最后两层上,且倒数第二层是满的,则这颗树是平衡的。
如果一颗平衡树最后一层的所有叶子结点都在最靠左的位置上,则称这颗树是左平衡的。可以利用左平衡二叉树来帮助实现堆和优先级队列。