图算法--最短路径算法的实现与应用

最短路径

在解决网络路由的问题中，寻找图中一个顶点到另一个顶点的最短路径或最小带权路径是非常重要的过程。

正式表述为，给定一个有向带权图G=(V,E)，顶点s到V中顶点t的最短路径为在E中边的集合S中连接s到t代价最小的路径。

当找到S时，我们就解决了单对顶点最短路径问题。要做到这一点，实际上首先要解决更为一般的单源最短路径问题，单源最短路径问题是解决单对顶点最短路径过程中的一部分。在单源最短路径问题中，计算从一个顶点s到其他与之相邻顶点之间的最短路径。之所以要用这个方法解决此问题是因为没有其他更好的办法能用来解决单对顶点最短路径问题。

Dijkstra算法

解决单源最短路径问题的方法之一就是Dijkstra算法。

Dijkstra算法会生成一棵最短路径树，树的根为起始顶点s，树的分支为从顶点s到图G中所有其他顶点的最短路径。此算法要求图中所有的权值均为非负数。与Prim算法一样，Dijkstra算法也是一种利用贪心算法计算并最终能够产生最优结果的算法。

从根本上说，Dijkstra算法通过选择一个顶点，并不断地探索与此顶点相关的边，以此来确定每个顶点的最短路径最否是最优。此算法类似广度优先搜索算法，因为在往图中更深的顶点探寻之前首先要遍历与此顶点相关的所有顶点。为了计算s与其他所有顶点之前的最短路径，Dijkstra算法需要维护每个顶点的色值和最短路径估计。通常，最短路径估计由变量d表示。

开始，将所有色值设置为白色，最短路径估计设置为∞（代表一个足够大的数，大于图中所有边的权值）。将起始顶点的最短路径估计设置为0。随着算法的不断演进，在最短路径树中为每个顶点（除起始顶点）指派一个父结点。在算法结束之前，顶点的父结点可能会发生几次变化。

Dijkstra算法的运行过程如下：

首先，在图中所有白色顶点之间，选择最短路径估计值最小的顶点u。初始，最短路径估计值被设置为0的顶点将做为起始顶点。当选择此顶点后，将其涂成黑色。

接下来，对于每个与u相邻的顶点v，释放其边（u，v）。当释放边后，我们要确认是否要更新到目前为止所计算的最短路径。方法就是将（u，v）的权值加到u的最短路径估计中。如果这个合计值小于或等于v的最短路径估计，就将这个值指派给v，作为v的新最短路径估计。同时，将u设置为v的父结点。

重复这个过程，直到所有的顶点都标记为黑色。一旦计算完最短路径树，那么从s到另外一个顶点t的最短路径就能唯一确定：从树中t处的结点开始向随后的父结点查找，直到到达s。此寻找路径的反向路径即为s到t的最短路径。

下图展示了由a到图中其他顶点的最短路径的计算过程。例如，a到b的最短路径为（a，c，f，b），其权值为7。最短路径估计和每个顶点的父结点都显示在每个顶点的旁边。最短路径估计显示在斜线的左边，父结点显示在斜线的右边。浅灰色的边是最短路径树增长过程中的边。

 

 最短路径的接口定义

shortest

---

int shortest(Graph *graph, const PathVertex *start, List *paths, int (*match)(const void *key1, const void *key2));

返回值：如果计算最短路径成功，返回0；否则，返回-1。

描述：用于计算顶点start与有向带权图graph中其他所有顶点之间的最短路径。此操作会改变graph，所以如果有必要，在调用此操作之前先对图进行备份。

graph中的每个顶点必须包含PathVertex类型的数据。通过设置PathVertex结构体中的成员weight的值来指定每个边的权值，weitht的值由传入graph_ins_edge的参数data2决定。用PathVertex结构体的成员data来保存与顶点相关的数据，例如顶点的标识符。

graph的match函数（此函数在用graph_init对图进行初始化时调用）用来比较PathVertex结构体中的data成员。此函数与传入shortest中的参数match相同。

一旦计算完成，最短路径的相关信息将会返回给paths，paths是存储PathVertex结构体的列表。在paths中，起始顶点的父结点设置为NULL。而其他每个顶点的parents成员都指向位于该顶点之前的那个顶点，这个顶点位于从起始顶点开始的最短路径之上。paths中的顶点指向graph中的实际顶点，所以只要能够访问paths，函数调用都就必须要保证graph中的内存空间有效。一旦不再使用paths，就调用list_destroy来销毁paths。

复杂度：O（EV²），其中V是图中的顶点个数，E是边的条目数。

最短路径的实现与分析

为了计算有向带权图中一个顶点到其他所有顶点的最短路径，其图的表示方法与最小生成树中的表示方法相同。只是用PathVertex结构体取代顶点MstVertex结构。

PathVertex能够表示带树图，同时能够追踪Dijkstra算法所需要的顶点和边的信息。此结构体包含5个成员：data是与顶点相关的数据；weight是到达该顶点的边的权值；color是顶点的颜色；d是顶点的最短路径估计；parent是最短路径中顶点的交结点。

构造一个包含pathvertex结构体的图的过程与构造一个包含MstVertex结构体的图的过程相同。

shortest操作首先初始化邻接表结构链表中的每个顶点。将每个顶点的最短路径估计初始化为DBL_MAX（起始顶点除外，起始顶点的初始值为0.0）。用存储在邻接表结构链表中的顶点来维护顶点的色值、最短路径估计和父结点。其原因与计算最小生成树时的解释相同。

Dijkstra算法的核心是用一个单循环为图中的每个结点迭代一次。在每次的迭代过程中，首先在所选的白色顶点中选择最短路径估计最小的顶点。同时，在邻接表结构链表中将此顶点涂黑。接下来，遍历与所选顶点相邻的顶点。在遍历每个顶点时，检查它在邻接表结构链表中的颜色和最短路径估计。一旦获得了这些信息，就调用relax释放所选顶点与相邻顶点间的边。如果此过程中发现需要更新相邻顶点的最短路径估计和父结点，那么就在邻接表结构链表中更新此顶点。重复这个过程直到所有顶点都涂成黑色。

一旦Dijkstra算法中的主循环结束，计算图中起始顶点到所有其他顶点的最短路径的过程也就完成了。此时，将邻接表结构链表中每个黑色的PathVertex结构体插入链表paths中。在paths中，父结点为NULL的顶点就是起始顶点。其他每个顶点的parent成员都指向从起始顶点开始的最短路径中的前一个顶点。每个PathVertex结构体的成员weight并不经常使用，因为它只在存储到邻接表中时才用的到。下图展示了在上图1中计算最短路径时所返回的PathVertex结构体列表。

 

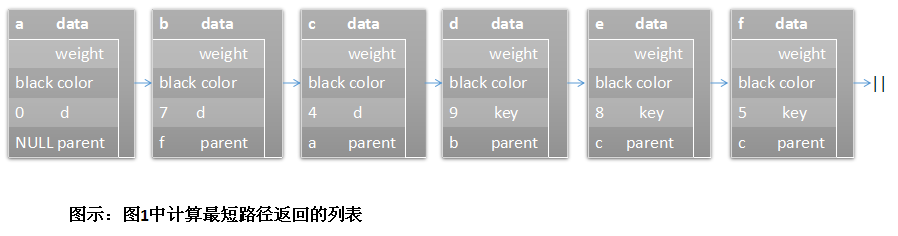
示例：计算最短路径的实现

/*shortest.c*/
#include <float.h>
#include <stdlib.h>

#include "graph.h"
#include "graphalg.h"
#include "list.h"
#include "set.h"

/*relax  释放边、更新最短路径估计值、更新父结点*/
static void relax(PathVertex *u, PathVertex *v, double weight)
{
    /*释放顶点u和v之间的边*/
    if(v->d > u->d + weight)
    {
        v-> = u->d + weight;
        v->parent = u;
    }
    return;
}

/*shortest  最短路径计算函数*/
int shortest(Graph *graph, const PathVertex *start, List *paths, int (*match)(const void *key1, const void key2))
{
    AdjList *adjlist;
    PathVertex *pth_vertex, *adj_vertex;

    ListElmt *element, member;
    double minimum;
    int found,i;

    /*初始化图中的所有顶点*/
    found = 0;

    for(element = list_head(&graph_adjlists(graph)); element != NULL; element = list_next(element))
    {
        pth_Vertex = ((AdjList *)list_data(element))->vertex;

        if(match(pth_vertex, start))
        {
            /*找到并初始化起始顶点*/
            pth_vertex->color = white;
            pth_vertex->d = 0;
            pth_vertex->parent = NULL;
            found = 1;
        }
        else
        {
            /*非起始顶点，初始化*/
            pth_vertex->color = white;
            pth_vertex->d = DBL_MAX;
            pth_vertex->parent = NULL;
        }
    }

    /*如果未匹配到起始顶点，程序退出*/
    if(!found)
        return -1;

    /*使用Dijkstra算法计算从起始顶点开始的最短路径*/
    i=0;

    while(i < graph_vcount(graph))
    {
        /*从所有的白色顶点中，选择最短路径估计值最小的顶点*/
        minimum = DBL_MAX;

        for(element=list_head(&graph_adjlists(graph)); element!=NULL; element = list_next(element))
        {
            pth_vertex = ((AdjList*)list_data(element))->vertex;

            if(pth_vertex->color == white && pth_vertex->d < minimum)
            {
                minimum = pth_vertex->d;
                adjlist = list_data(element);
            }
        }

        /*将该顶点涂成黑色*/
        ((PathVertex *)adjlist->vertex)->color = black;

        /*遍历与所选顶点相邻的顶点*/
        for(member=list_head(&adjlist->adjacent); member != NULL; member = list_next(member))
        {
            adj_vertex = list_data(member);

            for(element = list_head(&graph_adjlists(graph)); element != NULL; element = list_next(element))
            {
                pth_vertex = ((AdjList *)list_data(element))->vertex;

                if(match(pth_vertex, adj_vertex))
                {
                    relax(adjlist->vertex, pth_vertex, adj_vertex->weight);
                }
            }
        }
        i++;
    }
    /*将邻接表结构链表中每个黑色PathVertexx结构体插入链表paths中*/
    list_init(paths,NULL);

    for(element=list_head(&graph_adjlists(graph)); element!=NULL; element=list_next(paths,NULL))
    {
        /*加载邻接表结构链表中的每一个黑色顶点*/
        pth_vertex=((AdjList *)list_data(element))->vertex;

        if(pth_vertex->color == black)
        {
            if(list_ins_next(paths, list_tali(paths), pth_vertex) != 0)
            {
                list_destroy(paths);
                return -1;
            }
        }
    }
    return 0;
}

最短路径实例：路由表

最短路径算法在现实中一个很重要的应用是在互联网中对数据进行路由。路由是将数据从一个点传输到另一个点的决策过程。在互联网中，路由是沿着相互连接的点（称为网关）传播数据段或数据包的过程。在数据包通过一个网关时，路由器将会查看数据包最终目的地，然后将数据包发往下一个网关。路由器的目的就是将数据包往最接近于目的地的地方发送。

为了将数据包往最接近目的地的地方发送，每个路由器都要维护互联网的结构信息或拓扑信息。这些信息存储在路由表中。路由表为每个路由器知道如何到达的网关存储一个条目。每个条目指定把数据发送到下一个网关的地址。

由于路由器会周期性的随着互联网的变化更新其路由表，因此数据包会尽可能地沿着最佳路径传送数据。有一种类型的路由称为最短路径优先路由或SPF路由，其中每个路由器都维护有自己的网络图，以便它能通过计算自身与其他结点之间的最短路径来更新其路由表。互联网拓扑图是一个有向带权图，其顶点为网关，边为网关之间的连接线。边的权值由连接路径的性能决定。偶尔，路由器会交换拓扑和性能的信息，为此还专门设计了一种协议来完成此工作。

设计函数route，利用SPF路由算法计算更新路由表中条目所需要的信息。

该函数接受shortest的paths参数中返回的路径信息列表。

它使用此信息来确定路由器要把数据包发送到的下一个网关，以保证此网关离目的地更近了一步。

要为指定的网关完成一个完整的表，首先要调用函数shortest，其中网关由start参数传入。

接着，对于每个路由表中包含的目的地址，调用函数route，其中的目的地址由destination传入。

然后作为从paths生成的路径的图graph_init中所提供的match函数，把此地址传入match中。

route函数将目的列表paths中的父结点指针指向网关，同时返回一个传送数据包的最佳结点（此结点存放在输出参数next中）。next中返回的顶点指向paths中实际的顶点，所以只要还能访问next，paths中的内存空间就必须有效。

下图A部分展示了互联网中处于a的路由器的路由表的计算过程。B部分展示了处理b的路由器计算路由表的过程。注意，依据在互联网中起始位置的不同，其最短路径也不同。同样需要注意的是，在图B中是没办法到达a的，所以在该表中也没有相关条目。

计算路由的时间复杂度为O（n²），其中n为paths中的网关数目。

示例：路由表中更新条目的函数实现

/*route.c*/
#include <stdlib.h>
#include "graphalg.h"
#include "list.h"
#include "route.h"

/*route*/
int route(List *paths, PathVertex *destination, PathVertex **next, int (*match)(const void *key1, const void *key2))
{
    PathVertex *temp,
               *parent;
    ListElmt   *element;
    int        found;

    /*查找位于网关链表中的目的地址*/
    found = 0;

    for(element = list_head(paths); element != NULL; element = list_next(element))
    {
        if(match(list_data(element),destination))
        {
            temp = list_data(element);
            parent = ((PathVertex *)list_data(element))->parent;
            found = 1;
            break;
        }
    }

    /*如未发现目标地址，函数退出*/
    if(!found)
        return -1;

    /*计算到目的地最短路径的下一个网关*/
    while(parent!=NULL)
    {
        temp = list_data(element);
        found = 0;

        for(element = list_head(paths); element != NULL; element = list_next(element))
        {
            if(match(list_data(element),parent))
            {
                parent = ((PathVertex *)list_data(element))->parent;
                found = 1;
                break;
            }
        }

        /*如果目标不能到达，函数退出*/
        if(!found)
            return -1;
    }
    *next = temp;

    return 0;
}