数据库系统的设计者巧妙利用了磁盘预读原理:
将一个节点的大小设为等于一个页,这样每个节点需要一次I/O就可以完全载入
这是数据库最为重要且极为巧妙的设计。
为了达到这个目的,在实际实现B-Tree还需要使用如下技巧:
每次新建节点时,直接申请一个页的空间,这样就保证一个节点物理上也存储在一个页里,加之计算机存储分配都是按页对齐的,就实现了一个node只需一次I/O。
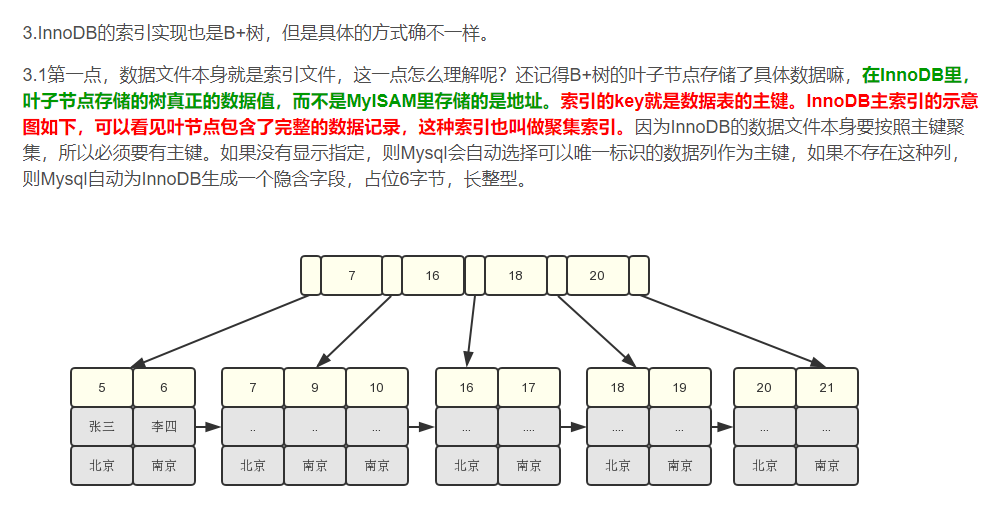
而B+树内把真实的数据全部放在了叶子节点中,非叶子节点中只存放了索引的数据,保证了数据项尽可能的多。保证树的高度。
定义:
描述一颗 B树时需要指定它的阶数,阶数 表示 此树的结点 最多 有 多少个孩子结点(子树),一般用字母 M 表示阶数。
M 阶的B树 :以【子树】讨论
- 上限:每个节点最多有 M 个子树
- 下限:
根节点至少2个子树,
非根节点至少有⌈M /2⌉个子树
所以也称 M 阶B树 为 ( ⌈M /2⌉ , M ) 树 ,即超级节点(除根节点)的子树数的上下限 。
注: 超级节点关键码的个数 = 节点子树数 - 1 。
例:
M = 4 阶,(2, 4)树。 最多含有 3个关键字 和 4个子树
M = 5 阶,(3, 5)树。 最多含有 4个关键字 和 5个子树
M = 6 阶,(3, 6)树。 最多含有 5个关键字 和 6个子树
- 1
- 2
- 3
所以,M阶 可理解为 M树,即内含(M-1)个关键字 和 M 个子树。
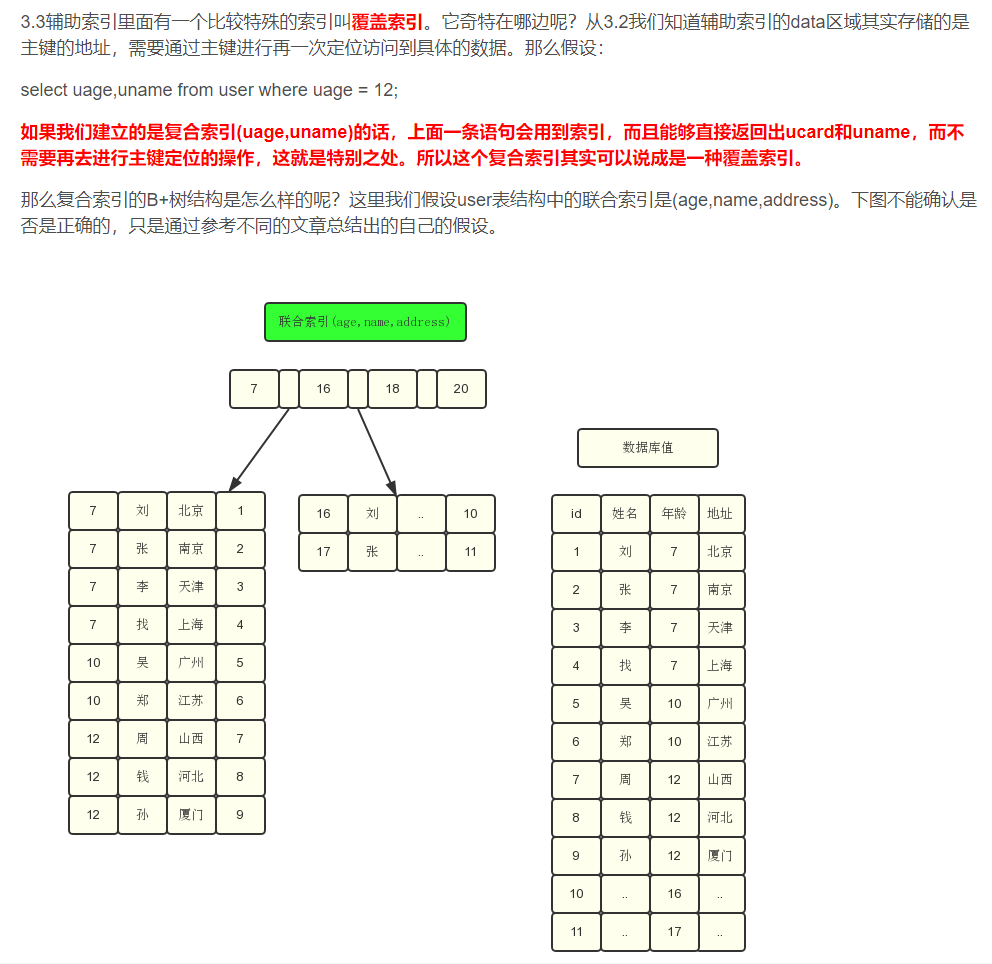
通过这个结构我们可以看见,在叶子节点中存储的数据是age,name,address的值(假设这些数据都是按照顺序排列好的,图中是随意写的),那么如果我们只想要这几个值的话,都不需要再进行主键定位查询了,提高了一些效率。
小结:
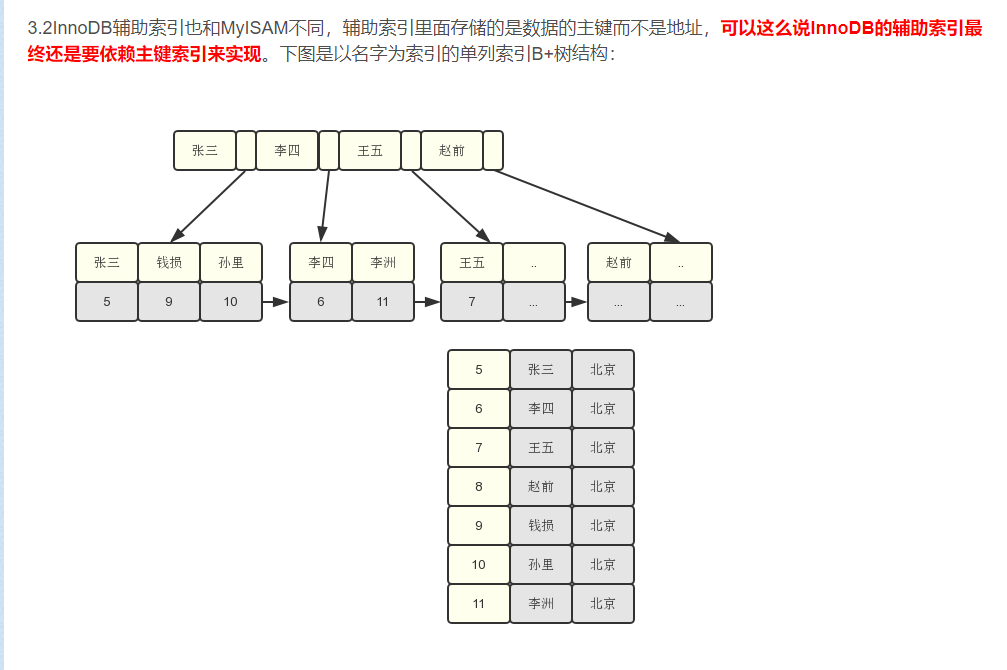
InnoDB的聚集索引是按照主键搜索,是最高效的,辅助索引需要走两次索引,首先查询辅助索引得到主键,再跟进主键查询获得记录。
问题1:不建议主键字段过长:原因上面第2点也讲过一些,过长会造成数据项空间变大,每个节点数据项数目变少,高度增加。
另外我们发现辅助索引的data域记录的也是主键,因此简介造成辅助索引变大,查询困难。
问题2:非单调字段:如果不是单调字段的话,会造成B+树不断的调整,十分低效,上一篇分析过插入和删除。使用自增字段的话会保持一个相对稳定的顺序。
1、内节点:非根非叶子节点,即非根的分支节点。
2、名称:B-树=B树=平衡多路查找树。
3、定义:m阶B树。
(0)、根节点孩子数rootChildNum范围:若没有孩子节点则孩子数为0,若有孩子则:2 <= rootChildNum <= m
(1)、树中每个节点的孩子树个数childNum范围:2 <= childNum <= m
(2)、内节点孩子个数innerChildNum的范围: ceil(m/2) <= innerChildNum <= m
(3)、节点数据个数dataNum与节点孩子个数childNum关系:childNum = dataNum + 1。而且数据递增排列。
(4)、所有叶子节点处于同一层次。
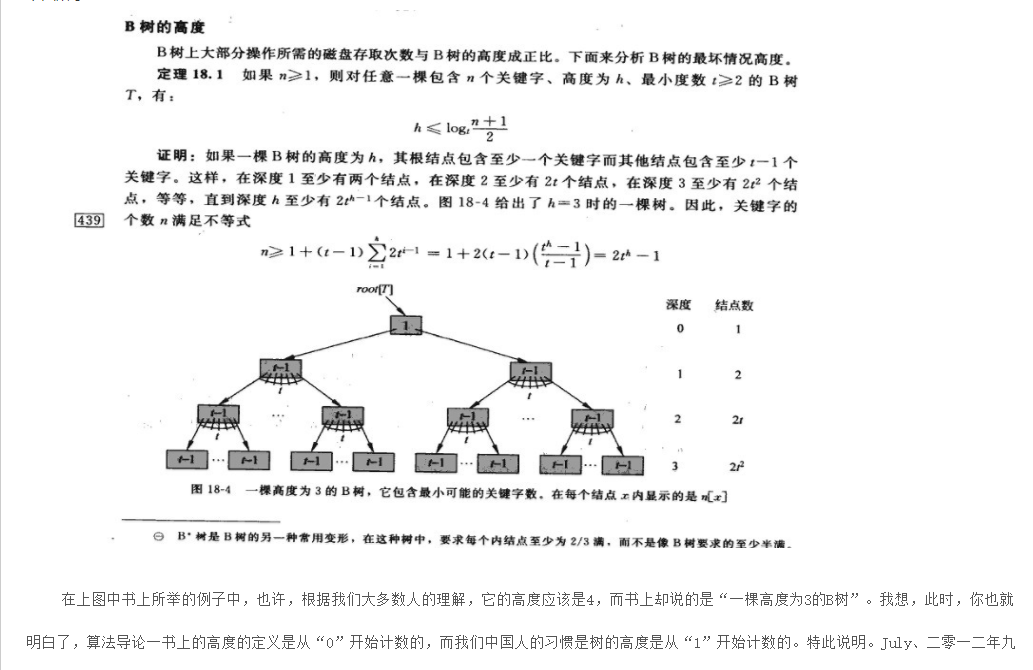
4、一颗B树的高度h与节点数n的不等关系建立:
第一层节点数:最少 1
第二层节点数:最少 2
第三层节点数:最少 2 × ceil(m/2)
第四层节点数:最少 2 × ceil(m/2) × ceil(m/2)
依次类推。。。。。。。。。
第h层节点数:最少 2 × [ ceil(m/2) ]h-2
因此高度为h的B树中节点树的最小值为: