目录
如何理解斜切 skew,先看一个 demo。在下面的 demo 中,有 4 个正方形,分别是
红色:不做 skew 变换,
绿色:x 方向变换,
蓝色:y 方向变换,
黑色:两个方向都变换,
拖动下面的滑块可以查看改变 skew 角度后的效果。切换 selector 可以设置 transform-origin,origin 默认是 0% 0%。大家可以把玩一下。
如果你把滑块拖到了 90deg 或者 - 90deg,那么你应该可以回答上面的问题了。如果你在 chrome 上看到整个页面变白,可以到隔壁 firefox 上试试,就这个 demo 而言,火狐是表现最好的, safari 最差。
用左扭,右扭来理解 skew 可能更加符合我们的直觉,但是却是不准确的。拿绿色正方形来说,origin 在 0% 0% 时,skew 20 度看起来像是往右扭,但是 origin 变成 100% 100% 时,看起来又像是往左扭了。
那么到底该怎么理解这个 skew 变换呢,其实它是矩阵 matrix 变换的一种。关于矩阵变换,张鑫旭老师的这篇文章讲解的不错,传送门,其中提到 skew 变化和通用 matrix 变换的对应关系:
也就是说 matrix 函数的第二三个参数来控制图形的斜切的,更通用一点,下面这个图展示了 css matrix 中的 6 个参数分别控制哪种变换,我们可以看一下:
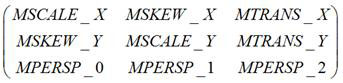
写到 matrix 函数里面如下:
有同学问了,为什么没有旋转的参数啊,其实旋转是 scale 和 skew 的组合操作。但是为了保证旋转后和原来的形状保持一致,4 个参数应该存在如下关系:
换句话说,旋转是一组特定的 scale + skew 组合操作。
理解坐标系
在了解到 skew 其实是一种矩阵变换后,我们来了解一下浏览器里的坐标系。因为除了 transform,其他操作都受坐标原点的影响。在浏览器中,向下为 Y 轴正方向,向右为 x 轴正方向,唯独原点是不确定的,而这正是 transform-origin 所起的作用。
当你设置这个属性为 top left 时,就是说矩阵变换坐标系的原点位于左上角,从而得到图形中的各个点的坐标,通过矩阵运算得到变换后的坐标,最后由浏览器渲染出来。设置为 50% 50% 则意味着坐标原点在图形的中心。
复合变换
思考下面两行 css:
对两个个正方形分别做上述变换,出来的效果是不同的,原因是因为上面两个操作,相当于对坐标进行两次矩阵乘法运算,不同于普通的乘法运算,矩阵乘法运算是不存在 ** 交换率 ** 的,所以结果会不同。
参考文章:
https://www.cnblogs.com/TianFang/p/3920734.html
https://code-industry.net/masterpdfeditor-help/transformation-matrix/
https://www.zhangxinxu.com/wordpress/2012/06/css3-transform-matrix-矩阵/
https://blog.csdn.net/u012964944/article/details/77824768
https://www.jianshu.com/p/956d54376338