PCA降维--两种实现 : SVD或EVD. 强力总结. 在鸢尾花数据集(iris)实做
今天自己实现PCA,从网上看文章的时候,发现有的文章没有搞清楚把SVD(奇异值分解)实现和EVD(特征值分解)实现,查阅多个文章很容易更糊涂,所以搞懂之后写下这个总结. 先说最关键的点:
a. PCA两个主要的实现方式: SVD(奇异值分解), EVD(特征值分解).
b. 特征值分解方式需要计算协方差矩阵,分解的是协方差矩阵.
SVD方式不需要计算协方差矩阵,分解的是经过中心化的原数据矩阵
1.特征值分解实现PCA (也有人称为PCA原始算法)

然后把中心化过的矩阵 X 乘 W, 就得到了低维数据.
2.SCD分解实现PCA
(1)样本中心化得到矩阵X
(2)对X进行SVD分解 u s v = svd(X)
(3)取v的前dd个分量
(4)X*v[0:dd]就是低维空间的数据.
(这是对应X每一行为一个样本的情况.u用于行数的压缩,v用于列数的压缩)
3.Show Me the Code
import numpy as np
from numpy.linalg import svd
from numpy.linalg import eig
from sklearn import datasets # 从sklearn中调出数据集
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
iris = datasets.load_iris()
data_src = iris.data #(150,4)
labels = iris.target #(150,)
d = 2 #设置低维空间维数
data_cen = data_src - np.mean(data_src,axis=0) # 样本中心化处理
# 用 SVD(奇异值分解) 做PCA
def pca_svd():
u, s, v = svd(data_cen)
pc_svd = np.dot(data_cen, v[:,0:2])
plt.scatter(pc_svd[:,0], pc_svd[:,1], c = labels)
plt.show()
return pc_svd
# 用 EVD(特征值分解) 做PCA
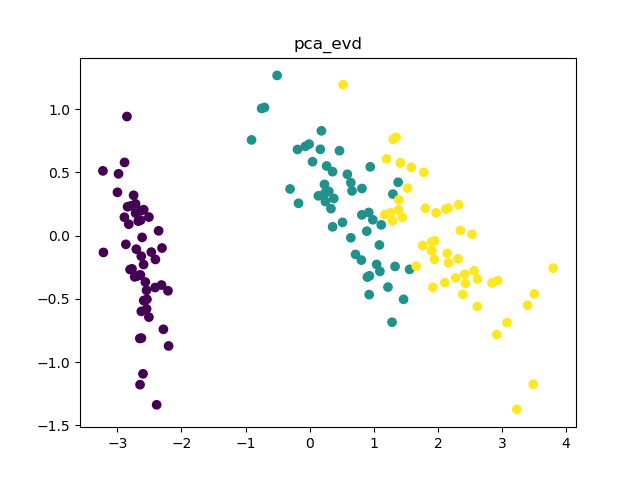
def pca_eig():
cov_mat = np.cov(data_cen,rowvar=0) #计算协方差矩阵,每行为一个样本
eigVals, eigVects = eig(cov_mat)
print(eigVects.shape)
eigValInd = np.argsort(eigVals)
eigValInd = eigValInd[: -(d + 1) : -1]
redEigVects = eigVects[:, eigValInd]
pc_eig = np.dot(data_cen, redEigVects)
plt.scatter(pc_eig[:,0], pc_eig[:,1], c = labels)
plt.show()
# 调用sk-learn库做PCA(内部也是用的SVD))
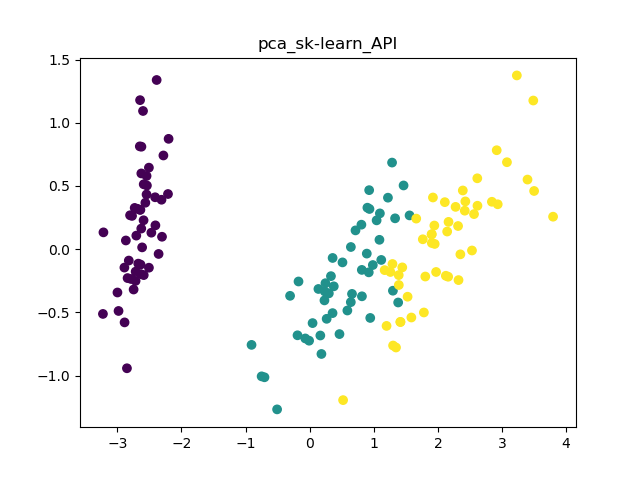
def pac_sk():
pca = PCA(n_components=2) #降到2维
pca.fit(data_cen) #训练
pc_sk=pca.fit_transform(data_cen) #降维后的数据
plt.scatter(pc_sk[:,0], pc_sk[:,1], c = labels)
plt.show()
pca_svd()
pca_eig()
pac_sk()
效果图:

4.详细理论知识传送门
以下是我学习过程中看的几篇高质量文章