最近上数据挖掘的课程,其中学习到了频繁模式挖掘这一章,这章介绍了三种算法,Apriori、FP-Growth和Eclat算法;由于对于不同的数据来说,这三种算法的表现不同,所以我们本次就对这三种算法在不同情况下的效率进行对比。从而得出适合相应算法的情况。
GitHub:https://github.com/loyalzc/freqpattern
(一)算法原理
其中相应的算法原理在之前的博客中都有非常详细的介绍,这里就不再赘述,这里给出三种算法大概的介绍
但是这里给出每个算法的关键点:
1.1 Apriori算法:
- 限制候选产生发现频繁项集
- 重要性质:频繁项集所有非空子集也一定是频繁的。
- 主要步骤:
- 连接
- 剪枝
- 特点:需要多次扫描数据库,对于大规模数据效率很低!
Apriori算法原理详细介绍:http://www.cnblogs.com/90zeng/p/apriori.html
1.2 FP-Growth算法
- 通过模式增长挖掘频繁模式
- 主要步骤:
- 构建频繁模式树
- 构造条件模式基
- 挖掘频繁模式
- 特点:两次扫描数据库,采用分治的策略有效降低搜索开销
FP-Growth算法原理详细介绍:http://www.cnblogs.com/datahunter/p/3903413.html
1.3 Eclat算法
- 使用垂直格式挖掘频繁项集
- 主要步骤:
- 将数据倒排{ item:TID_set }
- 通过求频繁k项集的交集来获取k+1项集
- 特点:仅需要一次扫描数据库,TID集合很长的话需要消耗大量的内存和计算时间
Eclat算法原理详细介绍:http://www.cnblogs.com/catkins/p/5270484.html
(二)算法实现
由于各个博客给出的算法实现并不统一,而且本人在实现《机器学习实战》中FP-Growth算法的时候发现,在在创建FP-Tree时根据headTable中元素的支持度顺序的排序过程中,这个地方的排序方法写的有问题,当在模式稠密时,具有很多支持度相同的项集,书中的代码并没有考虑着一点,所以如果遇到支持度相同的项集那个就会出现一定的随机性,导致建树过程出错,最后的频繁项集结果会偏小,因此这里对改错误进行了纠正,在支持度相同时,添加了按照项集排序的规则,这样建立的FP-Tree才完全正确。
1.1 Apriori算法实现:

1 # -*- coding: utf-8 -*- 2 ''' 3 @author: Infaraway 4 @time: 2017/4/15 12:54 5 @Function: 6 ''' 7 8 9 def init_c1(data_set_dict, min_support): 10 c1 = [] 11 freq_dic = {} 12 for trans in data_set_dict: 13 for item in trans: 14 freq_dic[item] = freq_dic.get(item, 0) + data_set_dict[trans] 15 # 优化初始的集合,使不满足最小支持度的直接排除 16 c1 = [[k] for (k, v) in freq_dic.iteritems() if v >= min_support] 17 c1.sort() 18 return map(frozenset, c1) 19 20 21 def scan_data(data_set, ck, min_support, freq_items): 22 """ 23 计算Ck中的项在数据集合中的支持度,剪枝过程 24 :param data_set: 25 :param ck: 26 :param min_support: 最小支持度 27 :param freq_items: 存储满足支持度的频繁项集 28 :return: 29 """ 30 ss_cnt = {} 31 # 每次遍历全体数据集 32 for trans in data_set: 33 for item in ck: 34 # 对每一个候选项集, 检查是否是 term中的一部分(子集),即候选项能否得到支持 35 if item.issubset(trans): 36 ss_cnt[item] = ss_cnt.get(item, 0) + 1 37 ret_list = [] 38 for key in ss_cnt: 39 support = ss_cnt[key] # 每个项的支持度 40 if support >= min_support: 41 ret_list.insert(0, key) # 将满足最小支持度的项存入集合 42 freq_items[key] = support # 43 return ret_list 44 45 46 def apriori_gen(lk, k): 47 """ 48 由Lk的频繁项集生成新的候选项集 连接过程 49 :param lk: 频繁项集集合 50 :param k: k 表示集合中所含的元素个数 51 :return: 候选项集集合 52 """ 53 ret_list = [] 54 for i in range(len(lk)): 55 for j in range(i+1, len(lk)): 56 l1 = list(lk[i])[:k-2] 57 l2 = list(lk[j])[:k-2] 58 l1.sort() 59 l2.sort() 60 if l1 == l2: 61 ret_list.append(lk[i] | lk[j]) # 求并集 62 # retList.sort() 63 return ret_list 64 65 66 def apriori_zc(data_set, data_set_dict, min_support=5): 67 """ 68 Apriori算法过程 69 :param data_set: 数据集 70 :param min_support: 最小支持度,默认值 0.5 71 :return: 72 """ 73 c1 = init_c1(data_set_dict, min_support) 74 data = map(set, data_set) # 将dataSet集合化,以满足scanD的格式要求 75 freq_items = {} 76 l1 = scan_data(data, c1, min_support, freq_items) # 构建初始的频繁项集 77 l = [l1] 78 # 最初的L1中的每个项集含有一个元素,新生成的项集应该含有2个元素,所以 k=2 79 k = 2 80 while len(l[k - 2]) > 0: 81 ck = apriori_gen(l[k - 2], k) 82 lk = scan_data(data, ck, min_support, freq_items) 83 l.append(lk) 84 k += 1 # 新生成的项集中的元素个数应不断增加 85 return freq_items
1.2 FP-Growth算法实现:
1)FP_Growth文件:
在create_tree()函数中修改《机器学习实战》中的代码:
##############################################################################################
# 这里修改机器学习实战中的排序代码:
ordered_items = [v[0] for v in sorted(local_data.items(), key=lambda kv: (-kv[1], kv[0]))]
##############################################################################################

1 # -*- coding: utf-8 -*- 2 """ 3 @author: Infaraway 4 @time: 2017/4/15 16:07 5 @Function: 6 """ 7 from DataMining.Unit6_FrequentPattern.FP_Growth.TreeNode import treeNode 8 9 10 def create_tree(data_set, min_support=1): 11 """ 12 创建FP树 13 :param data_set: 数据集 14 :param min_support: 最小支持度 15 :return: 16 """ 17 freq_items = {} # 频繁项集 18 for trans in data_set: # 第一次遍历数据集 19 for item in trans: 20 freq_items[item] = freq_items.get(item, 0) + data_set[trans] 21 22 header_table = {k: v for (k, v) in freq_items.iteritems() if v >= min_support} # 创建头指针表 23 # for key in header_table: 24 # print key, header_table[key] 25 26 # 无频繁项集 27 if len(header_table) == 0: 28 return None, None 29 for k in header_table: 30 header_table[k] = [header_table[k], None] # 添加头指针表指向树中的数据 31 # 创建树过程 32 ret_tree = treeNode('Null Set', 1, None) # 根节点 33 34 # 第二次遍历数据集 35 for trans, count in data_set.items(): 36 local_data = {} 37 for item in trans: 38 if header_table.get(item, 0): 39 local_data[item] = header_table[item][0] 40 if len(local_data) > 0: 41 ############################################################################################## 42 # 这里修改机器学习实战中的排序代码: 43 ordered_items = [v[0] for v in sorted(local_data.items(), key=lambda kv: (-kv[1], kv[0]))] 44 ############################################################################################## 45 update_tree(ordered_items, ret_tree, header_table, count) # populate tree with ordered freq itemset 46 return ret_tree, header_table 47 48 49 def update_tree(items, in_tree, header_table, count): 50 ''' 51 :param items: 元素项 52 :param in_tree: 检查当前节点 53 :param header_table: 54 :param count: 55 :return: 56 ''' 57 if items[0] in in_tree.children: # check if ordered_items[0] in ret_tree.children 58 in_tree.children[items[0]].increase(count) # incrament count 59 else: # add items[0] to in_tree.children 60 in_tree.children[items[0]] = treeNode(items[0], count, in_tree) 61 if header_table[items[0]][1] is None: # update header table 62 header_table[items[0]][1] = in_tree.children[items[0]] 63 else: 64 update_header(header_table[items[0]][1], in_tree.children[items[0]]) 65 if len(items) > 1: # call update_tree() with remaining ordered items 66 update_tree(items[1::], in_tree.children[items[0]], header_table, count) 67 68 69 def update_header(node_test, target_node): 70 ''' 71 :param node_test: 72 :param target_node: 73 :return: 74 ''' 75 while node_test.node_link is not None: # Do not use recursion to traverse a linked list! 76 node_test = node_test.node_link 77 node_test.node_link = target_node 78 79 80 def ascend_tree(leaf_node, pre_fix_path): 81 ''' 82 遍历父节点,找到路径 83 :param leaf_node: 84 :param pre_fix_path: 85 :return: 86 ''' 87 if leaf_node.parent is not None: 88 pre_fix_path.append(leaf_node.name) 89 ascend_tree(leaf_node.parent, pre_fix_path) 90 91 92 def find_pre_fix_path(base_pat, tree_node): 93 ''' 94 创建前缀路径 95 :param base_pat: 频繁项 96 :param treeNode: FP树中对应的第一个节点 97 :return: 98 ''' 99 # 条件模式基 100 cond_pats = {} 101 while tree_node is not None: 102 pre_fix_path = [] 103 ascend_tree(tree_node, pre_fix_path) 104 if len(pre_fix_path) > 1: 105 cond_pats[frozenset(pre_fix_path[1:])] = tree_node.count 106 tree_node = tree_node.node_link 107 return cond_pats 108 109 110 def mine_tree(in_tree, header_table, min_support, pre_fix, freq_items): 111 ''' 112 挖掘频繁项集 113 :param in_tree: 114 :param header_table: 115 :param min_support: 116 :param pre_fix: 117 :param freq_items: 118 :return: 119 ''' 120 # 从小到大排列table中的元素,为遍历寻找频繁集合使用 121 bigL = [v[0] for v in sorted(header_table.items(), key=lambda p: p[1])] # (sort header table) 122 for base_pat in bigL: # start from bottom of header table 123 new_freq_set = pre_fix.copy() 124 new_freq_set.add(base_pat) 125 # print 'finalFrequent Item: ',new_freq_set #append to set 126 if len(new_freq_set) > 0: 127 freq_items[frozenset(new_freq_set)] = header_table[base_pat][0] 128 cond_patt_bases = find_pre_fix_path(base_pat, header_table[base_pat][1]) 129 my_cond_tree, my_head = create_tree(cond_patt_bases, min_support) 130 # print 'head from conditional tree: ', my_head 131 if my_head is not None: # 3. mine cond. FP-tree 132 # print 'conditional tree for: ',new_freq_set 133 # my_cond_tree.disp(1) 134 mine_tree(my_cond_tree, my_head, min_support, new_freq_set, freq_items) 135 136 137 def fp_growth(data_set, min_support=1): 138 my_fp_tree, my_header_tab = create_tree(data_set, min_support) 139 # my_fp_tree.disp() 140 freq_items = {} 141 mine_tree(my_fp_tree, my_header_tab, min_support, set([]), freq_items) 142 return freq_items
2)treeNode对象文件

1 # -*- coding: utf-8 -*- 2 ''' 3 @author: Infaraway 4 @time: 2017/3/31 0:14 5 @Function: 6 ''' 7 8 9 class treeNode: 10 def __init__(self, name_value, num_occur, parent_node): 11 self.name = name_value # 节点元素名称 12 self.count = num_occur # 出现的次数 13 self.node_link = None # 指向下一个相似节点的指针,默认为None 14 self.parent = parent_node # 指向父节点的指针 15 self.children = {} # 指向孩子节点的字典 子节点的元素名称为键,指向子节点的指针为值 16 17 def increase(self, num_occur): 18 """ 19 增加节点的出现次数 20 :param num_occur: 增加数量 21 :return: 22 """ 23 self.count += num_occur 24 25 def disp(self, ind=1): 26 print ' ' * ind, self.name, ' ', self.count 27 for child in self.children.values(): 28 child.disp(ind + 1)
1.3 Eclat算法实现

1 # -*- coding: utf-8 -*- 2 """ 3 @author: Infaraway 4 @time: 2017/4/15 19:33 5 @Function: 6 """ 7 8 import sys 9 import time 10 type = sys.getfilesystemencoding() 11 12 13 def eclat(prefix, items, min_support, freq_items): 14 while items: 15 # 初始遍历单个的元素是否是频繁 16 key, item = items.pop() 17 key_support = len(item) 18 if key_support >= min_support: 19 # print frozenset(sorted(prefix+[key])) 20 freq_items[frozenset(sorted(prefix+[key]))] = key_support 21 suffix = [] # 存储当前长度的项集 22 for other_key, other_item in items: 23 new_item = item & other_item # 求和其他集合求交集 24 if len(new_item) >= min_support: 25 suffix.append((other_key, new_item)) 26 eclat(prefix+[key], sorted(suffix, key=lambda item: len(item[1]), reverse=True), min_support, freq_items) 27 return freq_items 28 29 30 def eclat_zc(data_set, min_support=1): 31 """ 32 Eclat方法 33 :param data_set: 34 :param min_support: 35 :return: 36 """ 37 # 将数据倒排 38 data = {} 39 trans_num = 0 40 for trans in data_set: 41 trans_num += 1 42 for item in trans: 43 if item not in data: 44 data[item] = set() 45 data[item].add(trans_num) 46 freq_items = {} 47 freq_items = eclat([], sorted(data.items(), key=lambda item: len(item[1]), reverse=True), min_support, freq_items) 48 return freq_items
(三)试验阶段:
这样我们就统一了三种算法的调用以及返回值,现在我们可以开始试验阶段了,我们在试验阶段分别根据最小支持度阈值和数据规模的变化来判断这三种算法的效率:
首先我们先统一调用者三个算法:
1 def test_fp_growth(minSup, dataSetDict, dataSet): 2 freqItems = fp_growth(dataSetDict, minSup) 3 freqItems = sorted(freqItems.iteritems(), key=lambda item: item[1]) 4 return freqItems 5 6 7 def test_apriori(minSup, dataSetDict, dataSet): 8 freqItems = apriori_zc(dataSet, dataSetDict, minSup) 9 freqItems = sorted(freqItems.iteritems(), key=lambda item: item[1]) 10 return freqItems 11 12 13 def test_eclat(minSup, dataSetDict, dataSet): 14 freqItems = eclat_zc(dataSet, minSup) 15 freqItems = sorted(freqItems.iteritems(), key=lambda item: item[1]) 16 return freqItems
然后实现数据规模变化的效率改变

1 def do_experiment_min_support(): 2 3 data_name = 'unixData8_pro.txt' 4 x_name = "Min_Support" 5 data_num = 1500 6 minSup = data_num / 6 7 8 dataSetDict, dataSet = loadDblpData(open("dataSet/" + data_name), ',', data_num) 9 step = minSup / 5 # ################################################################# 10 all_time = [] 11 x_value = [] 12 for k in range(5): 13 14 x_value.append(minSup) # ################################################################# 15 if minSup < 0: # ################################################################# 16 break 17 time_fp = 0 18 time_et = 0 19 time_ap = 0 20 freqItems_fp = {} 21 freqItems_eclat = {} 22 freqItems_ap = {} 23 for i in range(10): 24 ticks0 = time.time() 25 freqItems_fp = test_fp_growth(minSup, dataSetDict, dataSet) 26 time_fp += time.time() - ticks0 27 ticks0 = time.time() 28 freqItems_eclat = test_eclat(minSup, dataSetDict, dataSet) 29 time_et += time.time() - ticks0 30 ticks0 = time.time() 31 freqItems_ap = test_apriori(minSup, dataSetDict, dataSet) 32 time_ap += time.time() - ticks0 33 print "minSup :", minSup, " data_num :", data_num, 34 " freqItems_fp:", len(freqItems_fp), " freqItems_eclat:", len(freqItems_eclat), " freqItems_ap:", len( 35 freqItems_ap) 36 print "fp_growth:", time_fp / 10, " eclat:", time_et / 10, " apriori:", time_ap / 10 37 # print_freqItems("show", freqItems_eclat) 38 minSup -= step # ################################################################# 39 use_time = [time_fp / 10, time_et / 10, time_ap / 10] 40 all_time.append(use_time) 41 # print use_time 42 y_value = [] 43 for i in range(len(all_time[0])): 44 tmp = [] 45 for j in range(len(all_time)): 46 tmp.append(all_time[j][i]) 47 y_value.append(tmp) 48 plot_pic(x_value, y_value, data_name, x_name) 49 return x_value, y_value
然后实现最小支持度变化的效率改变

1 def do_experiment_data_size(): 2 3 data_name = 'kosarakt.txt' 4 x_name = "Data_Size" 5 data_num = 200000 6 7 step = data_num / 5 # ################################################################# 8 all_time = [] 9 x_value = [] 10 for k in range(5): 11 minSup = data_num * 0.010 12 dataSetDict, dataSet = loadDblpData(open("dataSet/"+data_name), ' ', data_num) 13 x_value.append(data_num) # ################################################################# 14 if data_num < 0: # ################################################################# 15 break 16 time_fp = 0 17 time_et = 0 18 time_ap = 0 19 freqItems_fp = {} 20 freqItems_eclat = {} 21 freqItems_ap = {} 22 for i in range(2): 23 ticks0 = time.time() 24 freqItems_fp = test_fp_growth(minSup, dataSetDict, dataSet) 25 time_fp += time.time() - ticks0 26 ticks0 = time.time() 27 freqItems_eclat = test_eclat(minSup, dataSetDict, dataSet) 28 time_et += time.time() - ticks0 29 ticks0 = time.time() 30 # freqItems_ap = test_apriori(minSup, dataSetDict, dataSet) 31 # time_ap += time.time() - ticks0 32 print "minSup :", minSup, " data_num :", data_num, 33 " freqItems_fp:", len(freqItems_fp), " freqItems_eclat:", len(freqItems_eclat), " freqItems_ap:", len(freqItems_ap) 34 print "fp_growth:", time_fp / 10, " eclat:", time_et / 10, " apriori:", time_ap / 10 35 # print_freqItems("show", freqItems_eclat) 36 data_num -= step # ################################################################# 37 use_time = [time_fp / 10, time_et / 10, time_ap / 10] 38 all_time.append(use_time) 39 # print use_time 40 41 y_value = [] 42 for i in range(len(all_time[0])): 43 tmp = [] 44 for j in range(len(all_time)): 45 tmp.append(all_time[j][i]) 46 y_value.append(tmp) 47 plot_pic(x_value, y_value, data_name, x_name) 48 return x_value, y_value
同时为了观察方便,我们需要对三种算法返回的结果进行绘图

1 # -*- coding: utf-8 -*- 2 """ 3 @author: Infaraway 4 @time: 2017/4/16 20:48 5 @Function: 6 """ 7 8 import matplotlib.pyplot as plt 9 10 11 def plot_pic(x_value, y_value, title, x_name): 12 plot1 = plt.plot(x_value, y_value[0], 'r', label='Kulc') # use pylab to plot x and y 13 plot2 = plt.plot(x_value, y_value[1], 'g', label='IR') # use pylab to plot x and y 14 # plot3 = plt.plot(x_value, y_value[2], 'b', label='Apriori') # use pylab to plot x and y 15 plt.title(title) # give plot a title 16 plt.xlabel(x_name) # make axis labels 17 plt.ylabel('value ') 18 plt.legend(loc='upper right') # make legend 19 20 plt.show() # show the plot on the screen
将两个部分统一执行:
1 if __name__ == '__main__': 2 3 # x_value, y_value = do_experiment_min_support() 4 # x_value, y_value = do_experiment_data_size() 5 # do_test()
(四)实验结果分析:
本次实验我们主要从以下几个方面来讨论三种算法的效率:
- 数据规模大小
- 最小支持度阈值
- 长事物数据
- 模式的稠密性
4.1 数据规模大小:
数据集:unxiData8
规模:900-1500
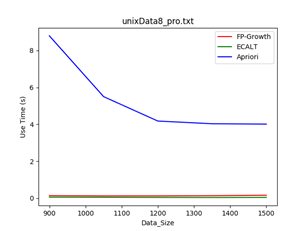
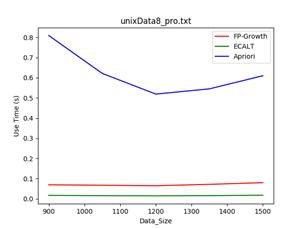
Min_support = 1/30时 Min_support = 1/20时
数据集:kosarakt
规模:6000-10000
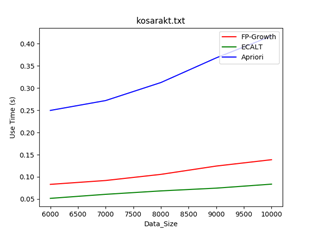
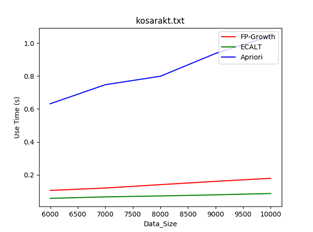

Min_support = 1/50 Min_support = 1/80 Min_support = 1/100
结论:一般情况下,数据规模越大,使用Apriori算法的效率越低,因为该算法需要多次扫描数据库,当数据量越大时,扫描数据库带来的消耗越多。
4.2 最小支持度大小
数据集:unixData8
支持度:4% - 20%
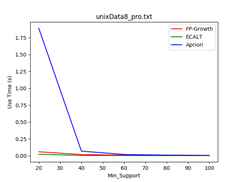
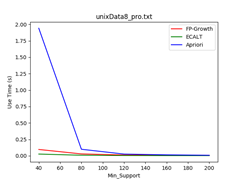
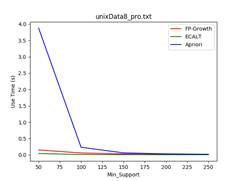
Data_size = 500 Data_size = 1000 Data_size = 1500
数据集:kosarakt
支持度:1% - 2%

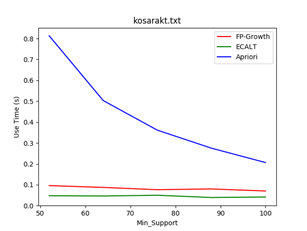

Data_size = 3000 Data_size = 5000 Data_size = 10000
结论:
- 最小支持度越小,各个算法所花费的时间越多且Apriori算法效率最差;
- Apriori算法候选项集较多,扫描数据库次数较多
- FP-Growth算法FP树较茂盛,求解模式更多
- Eclat算法求交集次数较多
- 随着最小支持度的增加,各个算法的效率逐渐接近,相当于数据量较小的情况。
4.3 长事物数据:
数据集:movieItem DataSize = 943
特点:单个事务数据比较长, 大量单个条目达到500个项(但频繁模式并不长)

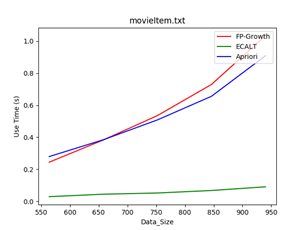

Min_support = 1/4 Min_support = 1/6 Min_support = 1/8
结论:对于长事物的数据集来说
- 最小支持度较大时,此时由于生成的FP树深度较大,求解的子问题较多,FP算法性能显著下降;
- 最小支持度较小时,此时Apriori算法生成大量候选项,扫描数据库次数显著增加,Apriori算法性能显著下降
4.4 模式稠密性:
数据集:movieItem
特点:单个事物间相似度很大(导致频繁模式特别多且比较长)
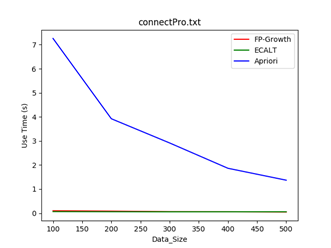

Min_support = 0.8 Min_support = 0.9
结论: 对于模式比较稠密的数据集来说,由于会产生特别多而且比较长的模式,三种算法的效率均有下降,其中FP-Growth算法中FP树层次较深,会产生较多的子问题,Eclat算法则需要进行大量的求交集运算,并且消耗大量的存储空间,Apriori算法则需要更多次的扫描数据库,因此效率最低。
(五)总结:
从上面实验可以看到,Apriori算法的效率最低,因为他需要很多次的扫描数据库;其次FP—Growth算法在长事物数据上表现很差,因为当事物很长时,树的深度也很大,需要求解的子问题就变得特别多,因此效率会迅速下降;Eclat算法的效率最高,但是由于我们事先使用了递归的思想,当数据量很大的时候会给系统带来巨大的负担,因此不适合数据量很大的情况;当然有一种叫做diffset的技术可以解决Eclat算法的不足,这里我们不做讨论!
本次实验的所有代码和数据下载:链接:http://pan.baidu.com/s/1jHAT7cq 密码:21pb
