1.<a>为a反复相乘生成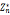 的子群,
的子群,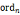 (a)为a在
(a)为a在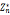 中的阶,phi为
中的阶,phi为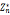 规模
规模
2.欧拉定理:对n>1,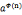 =1(modn),对所有a属于
=1(modn),对所有a属于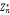 成立
成立
3.费马定理:p素数,,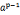 =1(modp) 对所有a属于
=1(modp) 对所有a属于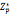 成立
成立
4.原根: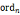 (g)=|
(g)=|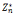 |,对模n,
|,对模n,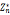 每个元素都是g的幂,g是
每个元素都是g的幂,g是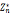 的原根或生成元
的原根或生成元
若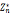 包含一个原根,则
包含一个原根,则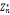 循环群
循环群
5.对所有素数p>2和正整数e,满足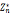 循环群n的值为2,4,
循环群n的值为2,4,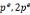
6.离散对数:g是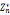 中的原根,a是
中的原根,a是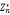 中任一元素,存在z使,
中任一元素,存在z使,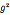 =a(modn),z称为离散对数,即
=a(modn),z称为离散对数,即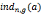
7.离散对数定理:g是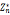 原根,则
原根,则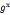 =
=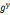 (modn)成立,当且仅当x=y(modφ(n))成立
(modn)成立,当且仅当x=y(modφ(n))成立
8.p 是奇素数且e>=1,则方程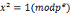 仅有两个解,x=1和x=-1
仅有两个解,x=1和x=-1
证明:
因为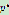 ,所以必有原根,设n=
,所以必有原根,设n=
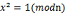 ,
,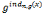 =
=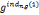 (modn),
(modn),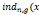 )=
)=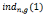 =0(modφ(n))
=0(modφ(n))
φ(n)=(p-1)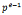 ,gcd(2,
,gcd(2,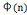 )=2,d=2,且0|2,有两个解,1,-1.
)=2,d=2,且0|2,有两个解,1,-1.
9.平凡平方根:1,-1
10.模n存在1的非平凡平方根,n是合数
11.反复平方法求数的幂(c无用),所需位操作次数O(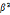 ) β为位数
) β为位数
注:下面代码多乘一个a的原因:
举例:a^10=a^5*a^5
a^5=a^2*a^2*a
MODULAR-EXPONENTIATION(a,b,n)
{
c =0;
d =1;
let<bk,bk-1,…,b0>be the binary represention of b;
for(i from k down to 0 )
c=2c;
d=(d*d)modn;
if(bi==1)
c=c+1;
d=(d*a)modn;
return d;
}
c语言的两种写法
1.递归
__int64 exp_mod(__int64 a, __int64 n, __int64 b)
{
__int64 t;
if(n==0) return 1%b;
if(n==1) return a%b;
t=exp_mod(a,n/2,b);
t=t*t%b;
if((n&1)==1) t=t*a%b;
return t;
}
2.递推
__int64 modexp(__int64 a,__int64 b,__int64 n)
{
__int64 ret=1;
__int64 tmp=a;
while(b)
{
//基数存在
if(b&0x1) ret=ret*tmp%n;
tmp=tmp*tmp%n;
b>>=1;
}
return ret;
}