TG可能会用到的动态规划-简易自学

---

最新更新

完整校订版见此

戳我阅读

以下为未核对不完整版本。

因版权原因，完整精校版不向所有公众开放。

请从您找到本博客的地址查找附带密码（比如简书分享了本网址，请您从简书分享页底部查询密码），感谢您的配合。

 

---

这里Pleiades_Antares小可爱qiumi

这几天突然回忆起来以前上的一个课qiumi

然后把当时上课做的笔记简单整理了一下发上来（主要是为了给自己复习orz）

于是就有了这个自学教程（基本上看着这个博客是完全可以学会1551）

希望能够帮助到正在拼命复习NOIP的你辣

没有学过动态规划的戳这个超级简单易懂的动态规划教程！！包教包会！

TG考试可能会用到的动态规划

by Pleiades_Antares

NOIP的例题大概会讲

NOIP2014 飞扬的小鸟

NOIP2017 宝藏

（还有更多的但是

NOIP对动态规划的考察主要在状态和转移方程的设计方面，往往设计出优秀的状态和转移即可在题目中取得不错的分数。

一、树形DP

树形DP用于解决树上问题。

状态常常用f（u，S）来表示已经对子树u这个子问题进行求解，状态为S的值。

转移往往会有子树合并。

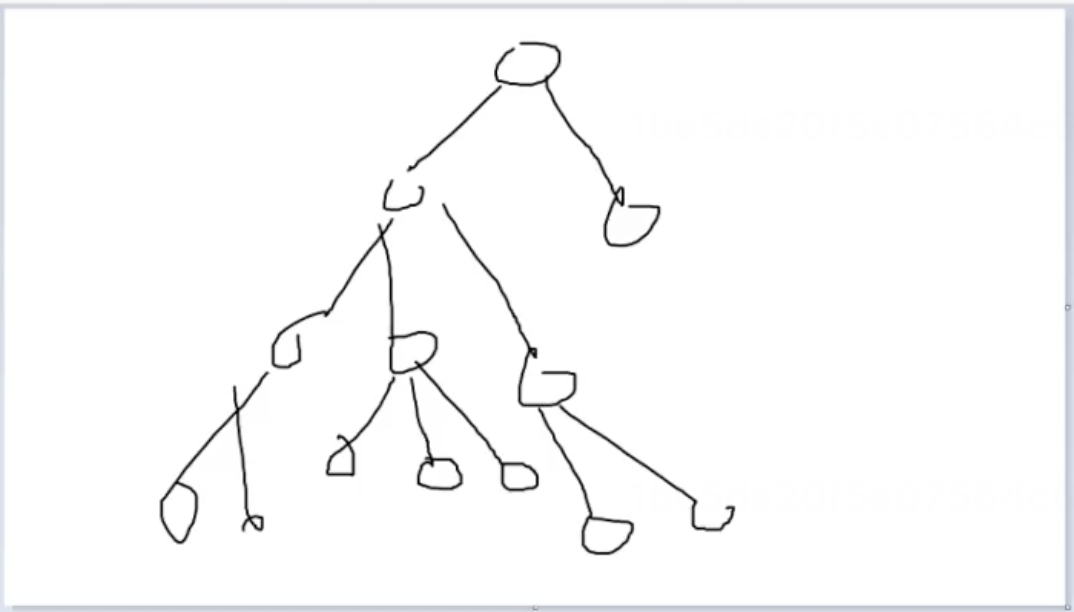
如上图所示，可以考虑通过这个我手绘的图片来辅助理解。

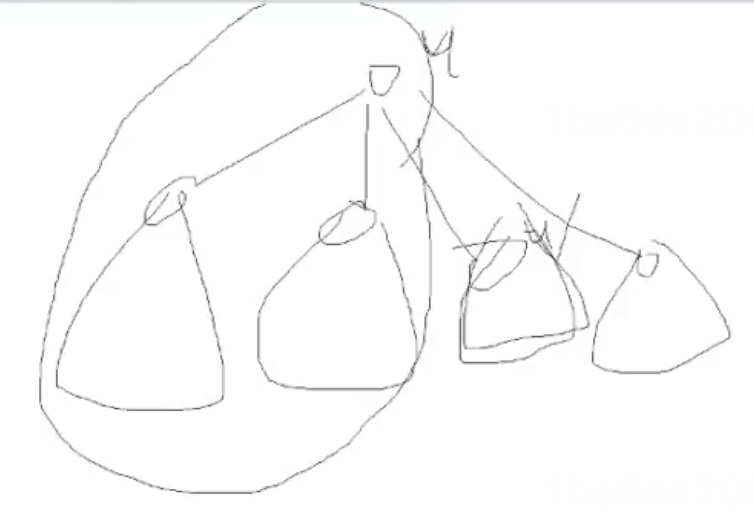
其代码常常如下所示：

dfs(u)
    initial f(u)
    foreach v in son[u]
        dfs(v)
        update f(u) with f(v)    

 解释下：

树的直径：

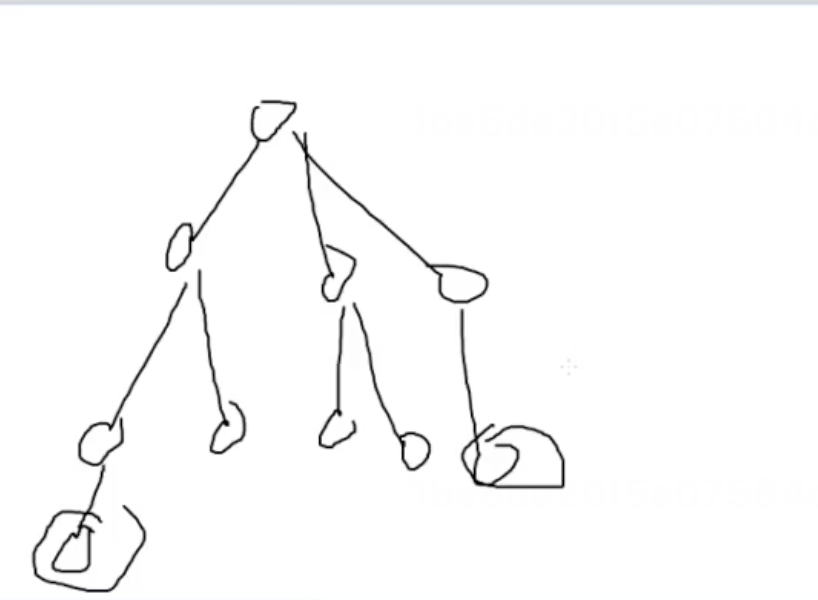
两个画了圈的点的距离即为树的直径。

f（u）表示以u为根的子树，到u的最长链的长度

来一道例题热身：

有一颗n个节点n-1条边的无向树，树上节点用1，2，.....n编号。

初始时每个节点都是白色。如果选中了节点u，则对于树中的每条边（u，v），v都会被染成黑色。注意u自身不会被染黑。

现在总共要选择恰好k个点，问有多少种方法使得所有节点被染黑。

数据范围：1<=n<=100000,1<=k<=min(n,100)

先考虑n<=1000时要怎么做？

令dp(u,k,color,choice)表示对于以u为根的子树，里面选了k个点，u的颜色为黑/白，u有没有被选中。u子树外点的选择只能影响到u子树中u点的颜色，

u子树只有u点的选择情况能影响到u子树外的点的颜色。所以这样的状态时足够的。

时间复杂度：O（nk²）

dp[u][k][color][choice]
t[k][color][choice]

void dfs(int u) {
    dp[u][1][0][1] = 1;
    dp[u][0][0][0] = 1;
    for (int v: son[u]) {
        dfs(v);
        for (int uk = 0; uk <= k; ++uk) {
            for (int vk = 0; vk <= k; ++vk) {
                for (int ucolor = 0; ucolor < 2; ++ucolor) {
                    for (int vcolor = 0; vcolor < 2; ++vcolor) {
                        for (int uchoice = 0; uchoice < 2; ++uchoice) {
                            for (int vchoice = 0; vchoice < 2; ++vchoice) {
                                t[uk + vk][u_new_color][uchoice] += dp[u][uk][ucolor][uchoice] * dp[v][vk][vcolor][vchoice]
                            }
                        }
                    }
                }
            }
        }
    }
}

//尝试在用u的孩子v的dp数组f（v）更新f（u）的时候，只枚举f（u）

实际上，时间复杂度是O（nk）而非O（nk²）

这就是——01背包实际上。

关于01背包的模板可以参考这篇文章，网上也有很多其他大神有关于01背包的理解，这里就不再赘述。

把std源代码发出来：

#include <bits/stdc++.h>

using namespace std;

const int maxn = 1e5 + 10, maxk = 110, mod = 1e9 + 7;

void judge() {
    freopen("action.in", "r", stdin);
    freopen("action.out", "w", stdout);
    return;
}

int n, k, siz[maxn], q[maxn], par[maxn], fnt, rar, ans;
int dp[maxn][maxk][2][2], pd[maxk][2][2];
vector<int> g[maxn];

inline void Add(int &x, int y) {
    x = x + y < mod ? x + y : x + y - mod;
    return;
}

int main() {
    judge();
    scanf("%d%d", &n, &k);
    for (int i = 1; i < n; ++i) {
        int u, v;
        scanf("%d%d", &u, &v);
        g[u].push_back(v);
        g[v].push_back(u);
    }
    q[rar++] = 1;
    while(fnt != rar) {
        int u = q[fnt++];
        siz[u] = 1;
        dp[u][0][0][0] = dp[u][1][1][0] = 1;
        for (int i = 0; i < g[u].size(); ++i) {
            int &v = g[u][i];
            if(v != par[u]) {
                par[q[rar++] = v] = u;
            }
        }
    }
    for (int ti = rar - 1; ti; --ti) {
        int &u = q[ti], &p = par[u], Endu = min(siz[u], k), Endp = min(siz[p], k);
        for (int ip = 0; ip <= Endp; ++ip) {
            for (int xp = 0; xp < 2; ++xp) {
                for (int yp = 0; yp < 2; ++yp) {
                    pd[ip][xp][yp] = dp[p][ip][xp][yp];
                    dp[p][ip][xp][yp] = 0;
                }
            }
        }
        for (int ip = 0; ip <= Endp; ++ip) {
            for (int xp = 0; xp < 2; ++xp) {
                for (int yp = 0; yp < 2; ++yp) {
                    static int s;
                    if(s = pd[ip][xp][yp]) {
                        int End = min(Endu, k - ip);
                        for (int iu = 0; iu <= End; ++iu) {
                            for (int xu = 0; xu < 2; ++xu) {
                                for (int yu = xp ^ 1; yu < 2; ++yu) {
                                    Add(dp[p][iu + ip][xp][yp | xu], (long long) s * dp[u][iu][xu][yu] % mod);
                                }
                            }
                        }
                    }
                }
            }
        }
        siz[p] += siz[u];
    }
    for (int xu = 0; xu < 2; ++xu) {
        Add(ans, dp[1][k][xu][1]);
    }
    printf("%d
", (ans + mod) % mod);
    return 0;
}

二、数位DP

如果题目给定了一个很大的数字，问你有多少符合一系列与

例题：

定义 S(n) 为将 n在 10 进制下的所有数位从小到大排序后得到的数。例如：S(1)=1, S(50394)=3459, S(323) =233

给定 X 求取模的结果。 

数据范围：1<=X<=10⁷⁰⁰.

考虑如何计算答案，可以通过分别计算每一位对总和的贡献来求。定义 cnt(i, x)为 S(1),S(2),...,S(X)中第i位为x 的数量。

直接求 cnt(i, x)仍然较为困难，考虑差分。令dlt(i, x) 为第 i 位上有多少个数 ≥ x。对于一个 S(y) 中第 i 位 ≥ x 的数 y，可以发现其必须满足有至少 i 个数位 ≥ x，这样就可以进行dp了。

另 dp(i, j, x, cmp) 表示填了前 i位，有至少 j个数字≥ x，与 N 的大小关系位cmp。

转移时直接枚举第i + 1 位数字是多少即可。

三、状压DP

解决状态较为复杂的问题，时间复杂度常常是指数级别。

（qwq我真的列不出来只能放截图了）

S = 1 << n;
for (int s = 0; s < S; ++s) {
    for (int t = s; ; t = (t - 1) & s) {
    ...
    if(t == 0) break;
    }
}

来一道例题

再来一道例题：

NOIP2014

飞扬的小鸟

思路详解⬇️

NOIP2017 宝藏

先看一下题目：

参与考古挖掘的小明得到了一份藏宝图，藏宝图上标出了 nn 个深埋在地下的宝藏屋，也给出了这 nn个宝藏屋之间可供开发的 mm 条道路和它们的长度。

小明决心亲自前往挖掘所有宝藏屋中的宝藏。但是，每个宝藏屋距离地面都很远，也就是说，从地面打通一条到某个宝藏屋的道路是很困难的，而开发宝藏屋之间的道路则相对容易很多。

小明的决心感动了考古挖掘的赞助商，赞助商决定免费赞助他打通一条从地面到某个宝藏屋的通道，通往哪个宝藏屋则由小明来决定。

在此基础上，小明还需要考虑如何开凿宝藏屋之间的道路。已经开凿出的道路可以任意通行不消耗代价。每开凿出一条新道路，小明就会与考古队一起挖掘出由该条道路所能到达的宝藏屋的宝藏。另外，小明不想开发无用道路，即两个已经被挖掘过的宝藏屋之间的道路无需再开发。

新开发一条道路的代价是：

这条道路的长度 xx 从赞助商帮你打通的宝藏屋到这条道路起点的宝藏屋所经过的宝藏屋的数量（包括赞助商帮你打通的宝藏屋和这条道路起点的宝藏屋）。

请你编写程序为小明选定由赞助商打通的宝藏屋和之后开凿的道路，使得工程总代价最小，并输出这个最小值。

 这道题有很多种做法（雾）

放一个正确的代码（DP）

#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cmath>
#include <iostream>
#include <algorithm>
#include <set>
#include <queue>
#include <map>
#include <vector>
#include <utility>
#include <string>
#include <functional>

#define rep(i, n) for(int i = 0; i < (n); ++i)
#define forn(i, l, r) for(int i = (l); i <= (r); ++i)
#define per(i, n) for(int i = (n) - 1; i >= 0; --i)
#define nrof(i, r, l) for(int i = (r); i >= (l); --i)
#define SZ(x) ((int)(x).size())
#define ALL(x) (x).begin(), (x).end()
#define mp make_pair
#define pb push_back
#define X first
#define Y second

using namespace std;

typedef long long LL;
typedef pair<int, int> pii;

const int maxn = 12, maxs = 1 << 12, oo = 1e9 + 7;

int n, m, g[maxn][maxn], h[maxn][maxs];
int dp[maxn][maxs], f[maxs][maxs];

void judge() {
    freopen("treasure.in", "r", stdin);
    freopen("treasure.out", "w", stdout);
    return;
}

inline bool chkmin(int &x, const int &y) {
    return x > y ? x = y, 1 : 0;
}

int main() {
//    judge();
    scanf("%d%d", &n, &m);
    if(n == 1) {
        puts("0");
        return 0;
    }
    rep(i, n) {
        rep(j, n) {
            g[i][j] = oo;
        }
        g[i][i] = 0;
    }
    while(m--) {
        int u, v, w;
        scanf("%d%d%d", &u, &v, &w);
        --u;
        --v;
        if(w < g[u][v]) {
            g[u][v] = g[v][u] = w;
        }
    }
    m = 1 << n;
    rep(i, n) {
        rep(s, m) {
            if((s >> i) & 1) {
                continue;
            }
            h[i][s] = oo;
            rep(j, n) {
                if((s >> j) & 1) {
                    chkmin(h[i][s], g[i][j]);
                }
            }
        }
    }
    rep(s, m) {
        int T = m - 1 ^ s;
        for (int t = T; t; t = (t - 1) & T) {
            rep(i, n) {
                if((s >> i) & 1) {
                    if(h[i][t] == oo) {
                        f[s][t] = oo;
                        break;
                    }
                    f[s][t] += h[i][t];
                }
            }
        }
    }
    rep(i, n) {
        rep(s, m) {
            dp[i][s] = oo;
        }
    }
    rep(i, n) {
        dp[0][1 << i] = 0;
    }
    int tmp;
    rep(i, n - 1) {
        rep(s, m) {
            if((tmp = dp[i][s]) < oo) {
//                printf("dp[%d][%d] = %d
", i, s, tmp);
                int T = m - 1 ^ s;
                for (int t = T; t; t = (t - 1) & T) {
                    if(f[t][s] != oo) {
                        chkmin(dp[i + 1][s | t], tmp + f[t][s] * (i + 1));
                    }
                }
            }
        }
    }
    --m;
    int ans = oo;
    rep(i, n) {
        chkmin(ans, dp[i][m]);
    }
    printf("%d
", ans);
    return 0;
}

有 30000个岛屿从左到右排列，有 n个宝石，在 p1​, p2​, ..., pn​上。 你初始时在 0 号岛上，第一次跳到 d 号岛上，第i (i > 2)次你向右跳跃的距离为第i − 1次跳跃距离 l 或者 l-1 或者l + 1。问最多能拿多少宝石。

数据范围：1 ≤ n, d ≤ 30000。

再看一道题：