最大似然估计的目标是获取模型中的参数。前提是模型已经是半成品,万事俱备只欠参数。此外,对样本要求独立同分布(参数就一套)
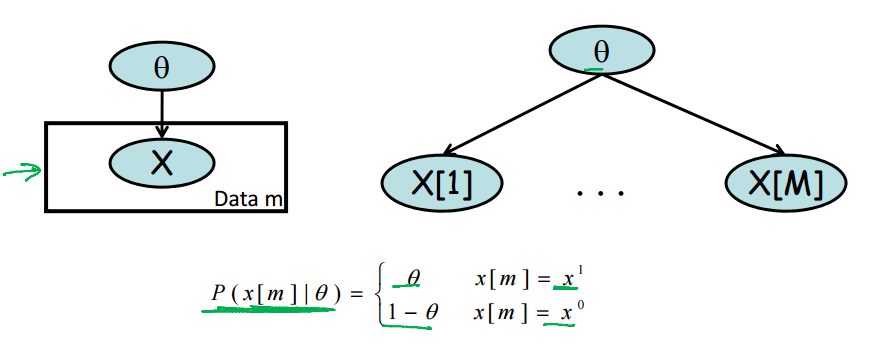
上图中x ~ B(theta). 样本数为M.
最大似然估计用似然函数作为优化目标,参数估计的过程为寻优过程。一般情况下认为,如果该参数使得数据发生的可能性最大,则该参数为最可能的一组参数。数学表达为下图: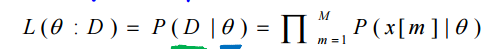
1、充分统计
充分统计是从样本映射到某个向量的一个公式。这个公式必须满足甲样本映射结果的和,必须与乙样本映射结果的和相同。而且这个必须成立,与总体分布的参数无关。例子:样本均值,样本方差。
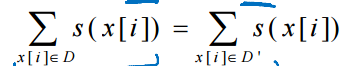
这种求和一致性如果设计合理的情况下, 可以直接导出参数的 表达式
比如在投硬币的统计模型中,T与H各自的数目就是充分统计量
又比如在估计骰子的bias的统计模型中,我们只在乎各个数字出现的次数,而不在乎顺序。此时的充分统计量为骰子的数字
在高斯模型中,可做以下分解:

如果观测到x不同的值,则可断定,1,x,x^2,是充分统计量。
2、参数的极大似然估计
在充分统计的条件下,参数的极大似然估计有着优雅的解析解。

3、贝叶斯网络中的极大似然估计
3.1、独立参数的贝叶斯网络
在极大似然估计的观点中,参数是随机变量,其有着自己的模型。如果考虑一个概率图模型,那么在对参数进行估计时就必须考虑随机变量之间的交互关系。一个简单的未知参数贝叶斯网络如图所示:
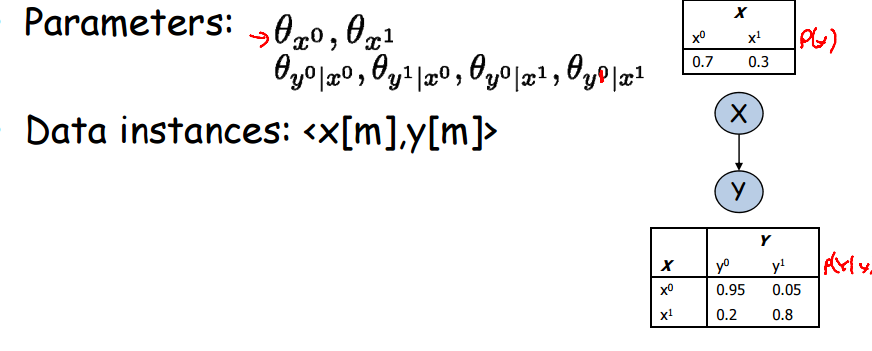
待估计的参数为theta_x,theta_y|x. 其中theta_x有两个取值,theta_y|x有四个取值。其解析表达式如下图:

第二步使用了链式分解,第四步将参数进行分开表达。更一般的,有下式:

第三部对调乘法,则后面简化为局部似然函数(某个随机变量的似然函数)。如果每个节点都有自己的独立参数,则最终的似然函数为局部似然函数的乘积。如果为表式CPD,则概率值就是参数值,那么又可简化为下式:
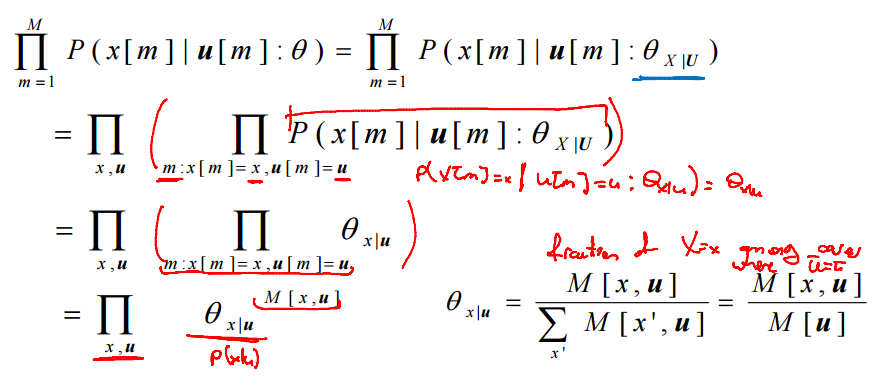
故对于表式CPD的贝叶斯网络,theta_x|parents = x出现的次数/父节点总数(边际所有x的可能性)
3.2 共享参数贝叶斯网络
共享参数贝叶斯网络往往描述一个转移过程。机器人直走有一定概率走偏,方向偏了继续直走,下次走偏的模式依旧是一定的。估计“走偏函数”的参数实际上是用的就是共享参数贝叶斯网络。
共享参数贝叶斯网络不能直接看作独立参数贝叶斯网络的特例。因为其要多一条限制即参数均相等。如果依旧使用独立参数贝叶斯模型,则参数无法统一。
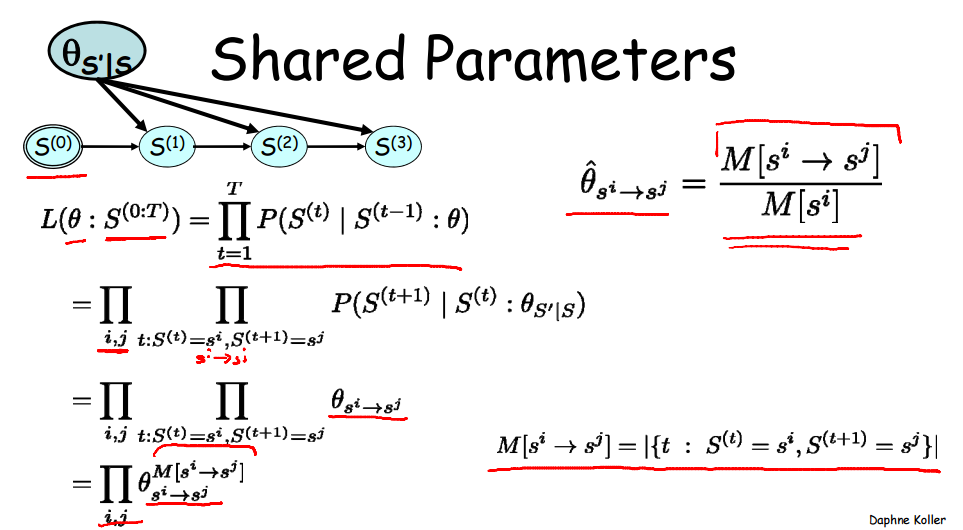
上述模型中s~B(0,1),故theta共有4种:0-1,0-0,1-1,1-0.
第二步中,总次数T被分解成上述四种情况。ij实际表达的是i->j。一个更复杂些的共享参数贝叶斯网络如图:
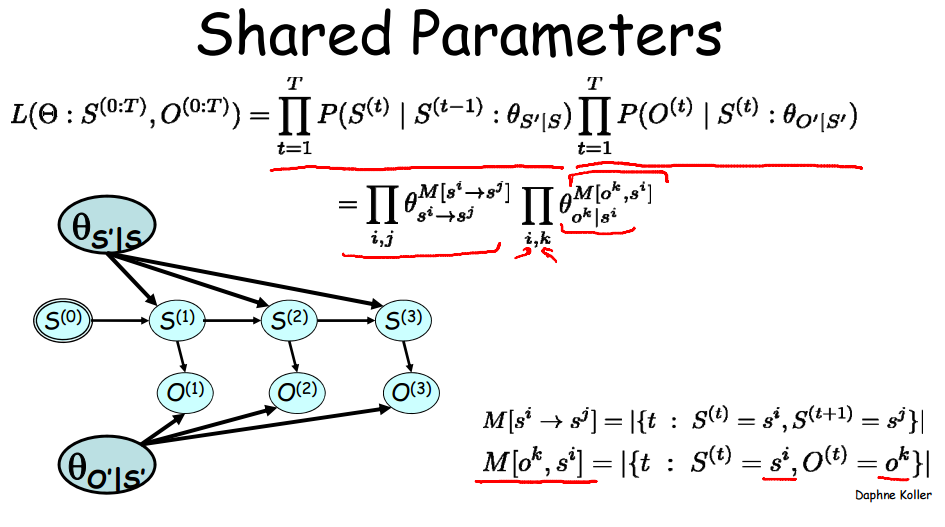
4、小技巧
当样本不大时,使用简单而错误的网络效果可能比复杂但正确的网络好。原因是网络复杂了容易对数据进行过拟合。