算法-位运算-1

1. 不用比较判断找出AB中较大的数

public class getMaxWithOutCompair {
    public int flip(int n) {
        return n ^ 1;
    }

    public int sign(int n) {
        // 如果负数返回0 如果正数返回1
        return flip((n >> 31) & 1);
    }

    public int getMax(int a, int b) {
　　　　　　// 这里可能溢出
        int c = a - b;
        int sign = sign(c);
        int flip = flip(sign);
        return a * sign + b * flip;
    }
}

 public int getMax2(int a, int b) {
        int sa = sign(a); // 正数返回1 负数返回0
        int sb = sign(b); // 正数返回1 负数返回0
        int sc = sign(a - b); // // 正数返回1 负数返回0
        int disSab = sa ^ sb; // a 和b的符号不一样返回1 符号一样返回0
        int sameSab = flip(disSab); // a 和b的符号不一样返回1 符号一样返回0
        int returnA = disSab * sa + sameSab * sc; // a 和b的符号不一样返回1 a正数返回1 a 
        // 和b的符号不一样返回1 正数返回1
        int returnB = flip(returnA);
        return a * returnA + b * returnB;

    }

2. 32位的数判断是否是2的幂 4的幂

2的幂的二进制特性 只有一位上是1其余都是0

取二进制数上最右的1的位置

N&((~N)+1) 

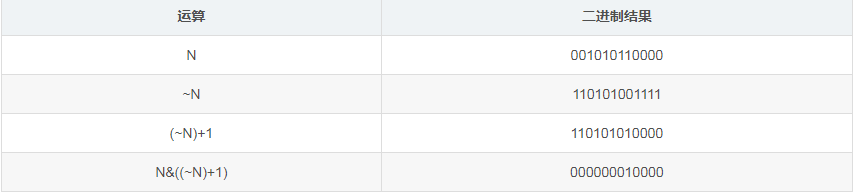
1. 求数的最右1 判断两个数是否相等

2. 数 & 数-1等于0 说明是2 的幂次方数

4的幂次方二进制数特征 二进制位上只有一个1,1的位置在0 2 4 6位置上

4的幂一定是2的幂

先判断二进制位上只有一个1再

数 & 0101 0101 0101 0101 0101 0101 0101 0101 (0x55555555)不等于0 是4的幂次方数

3. 不使用算数运算符 实现a和b的加减乘除

^ 代表无进位相加

& 左移1位代表进位信息

数取反+1 就是数的反数

/**
 * 不使用运算符 执行加减乘除运算
 * <p>
 * 加减乘除
 * add , subtract , multiply and divide
 */
public class MathOperation {

    public int add(int a, int b) {
        int i = a;
        while (b != 0) {
            i = a ^ b; // 无进位相加
            b = (a & b) << 1; // 进位信息
            a = i;
        }
        return i;
    }

    public int subtract(int a, int b) {
        return add(a, negNum(b));
    }

    public int negNum(int a) {
        return add(~a, 1);
    }

　　　　// 跟十进制乘法一样的思路 只是换成二进制
    public int multiply(int a, int b) {
        int res = 0;
        while (b != 0) {
            if ((b & 1) != 0) {
                res = add(res, a);
            }
            a <<= 1;
            b >>>= 1;
        }
        return res;
    }

    public int divide(int a, int b) {
        int res = 0;
        for (int i = 31; i > -1; i = subtract(i, 1)) {
　　　　　　　　　　// a >> 1为了避免溢出 
            if ((a >> i) >= b) {
　　　　　　　　　　　　// 满足条件说明i位置上可以至为1
                res |= (1 << i);
　　　　　　　　　　　　// a减去b
                a = subtract(a, b << i);
            }
        }
        return res;
    }

}