先放模板

#include <bits/stdc++.h> using namespace std; const int maxn=100009; int head[maxn],cnt=1,dis[maxn][22],n,m,k; struct node{ int x,num,ci; bool operator < (const node&tmp) const{ return x>tmp.x; } }; struct p{ int to,nxt,w; }d[maxn]; void add(int u,int v,int w){ d[cnt].to=v,d[cnt].w=w, d[cnt].nxt=head[u],head[u]=cnt++; } priority_queue<node>q; int vis[maxn][22]; void dij(){ memset(dis,20,sizeof(dis)); dis[1][0]=0; node init;init.num=1,init.x=0;init.ci=0;q.push(init); while(!q.empty()) { node ans=q.top();q.pop(); if(vis[ans.num][ans.ci]) continue; vis[ans.num][ans.ci]=1; for(int i=head[ans.num];i;i=d[i].nxt) { //先在同样用ans.ci机会的那一层转移,此时要加边权d[i].w if(dis[d[i].to][ans.ci]>dis[ans.num][ans.ci]+d[i].w) { dis[d[i].to][ans.ci]=dis[ans.num][ans.ci]+d[i].w; node t;t.ci=ans.ci,t.num=d[i].to,t.x=dis[d[i].to][ans.ci]; q.push(t); } if(ans.ci>=k) continue; //用机会来转移,此时要求ans.ci比可用机会小,此时不加边权 if(dis[d[i].to][ans.ci+1]>dis[ans.num][ans.ci]) { dis[d[i].to][ans.ci+1]=dis[ans.num][ans.ci]; node t;t.ci=ans.ci+1,t.num=d[i].to,t.x=dis[d[i].to][ans.ci+1]; q.push(t); } } } } int main() { cin>>n>>m>>k; for(int i=1;i<=m;i++) { int l,r,w; cin>>l>>r>>w; add(l,r,w);add(r,l,w); } dij(); cout<<dis[n][k]; }
有一类这样的问题
分层图最短路在最短路的基础上,增加了一个条件:可将 n 条边的权值变为 0. 比如说下图:
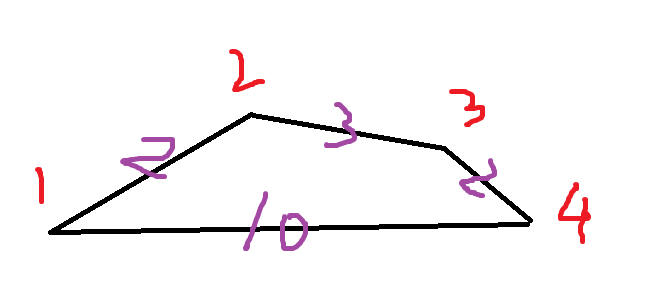
紫色为边权,红色是编号,很明显1到4的最短路是1->2->3一共是7
但是如果有一次免费将边权置为0的机会的话,那我们的最短路是1->4一共是0
那我们具体怎么来实现呢,实际上利用了动态规划的思想。
设dis[i][j]为走到i用了j次机会的状态
dis [ i ] [ j ] = min ( dis [ i ] [ j ] , dis [ k ] [ j ] +k到i的边权)
dis [ i ] [ j ] = min( dis [ i ] [ j ] , dis [ k ] [ j-1 ]) 因为此时我们用了一次机会,那么可以不加边权
那么在原来跑最短路的基础上,有了下面的代码

for(int i=head[ans.num];i;i=d[i].nxt) { //先在同样用ans.ci机会的那一层转移,此时要加边权d[i].w if(dis[d[i].to][ans.ci]>dis[ans.num][ans.ci]+d[i].w) { dis[d[i].to][ans.ci]=dis[ans.num][ans.ci]+d[i].w; node t;t.ci=ans.ci,t.num=d[i].to,t.x=dis[d[i].to][ans.ci]; q.push(t); } if(ans.ci>=k) continue; //用机会来转移,此时要求ans.ci比可用机会小,此时不加边权 if(dis[d[i].to][ans.ci+1]>dis[ans.num][ans.ci]) { dis[d[i].to][ans.ci+1]=dis[ans.num][ans.ci]; node t;t.ci=ans.ci+1,t.num=d[i].to,t.x=dis[d[i].to][ans.ci+1]; q.push(t); } }
