概念
树的直径:2点距离最远的路径.
结论
先说结论,对于一颗无根树,首先随便找一个点(u)开始进行搜索,找到离当前点最远的一点(s),然后从(s)开始搜最远的点(t)树的直径就为(s-t) 。
Ⅰ两遍(dfs||bfs)
证明
找到直径,我们只需找到直径2个端点其中的一个,然后找到离当前点最远的点即为另一个端点。
1.如果(u)在(s-t)的路径上,很明显是对的,到达(u)最远的点必为(s)或(t),因为是从(u)开始搜最远的点的。
2.如果(u)不在(s-t)的路径上,那么从(u)搜最远的点必然与(s-t)相交。
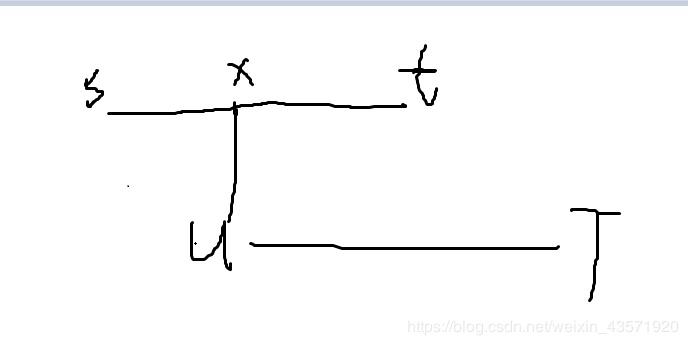
如图,如果u搜到最远的点为T,那么(dis(u,t) > dis(u,x) + dis(x,t))
很显然: (dis(s,t ) = dis(s,x) + dis(x,t) < dis(s,T) = dis(s,x) + dis(u,x) + dis(u,T))
所以 很容易得出必与直径相交,且搜到的点为另一个端点。
Ⅱ树型DP
设f[i]表示以i为根,到其子树的叶节点的最大距离。
考虑如何用子节点更新父节点,
当前点到叶节点的最大距离=(max){子节点到叶节点的距离+当前点到子节点的距离}。
设u为当前节点,v为u的子节点,(dis(u,v))是从u−>v这条路径上的距离
得到转移方程:
(f[u]=max){(f[v]+dis(u,v))}
如何维护以u为根的子树中的直径呢
以u为根子树的直径(=max){u到叶节点的最大距离+子节点到叶节点的最大距离+u到叶节点的距离}
然后我们钦定一个节点为根,比如1
得到转移方程:
(ans=max){(f[u]+f[v]+dis(u,v))}
ans即为树的直径
需要注意的是,我们要在更新f[u]之前更新ans,因为从u经过v到叶节点的路径是最长的路径,这样这条路径会被更新两次
这样做一定会选出u到叶节点最长的两条路径
void dp(int now)
{
vis[now]=1;
for(int i=head[now];i;i=d[i].nxt)
{
int v=d[i].to;
if(vis[v]) continue;
dp(v);
ans=max(ans,dis[now]+dis[v]+d[i].w);
dis[now]=max(dis[now],dis[v]+d[i].w);
}
}