LeetCode 131. 分割回文串 DFS DP

地址 https://leetcode-cn.com/problems/palindrome-partitioning/

给定一个字符串 s，将 s 分割成一些子串，使每个子串都是回文串。

返回 s 所有可能的分割方案。

示例:

输入: "aab"
输出:
[
  ["aa","b"],
  ["a","a","b"]
]

算法1
DFS 尝试各个回文组合 检测是否是回文 流程类似下图

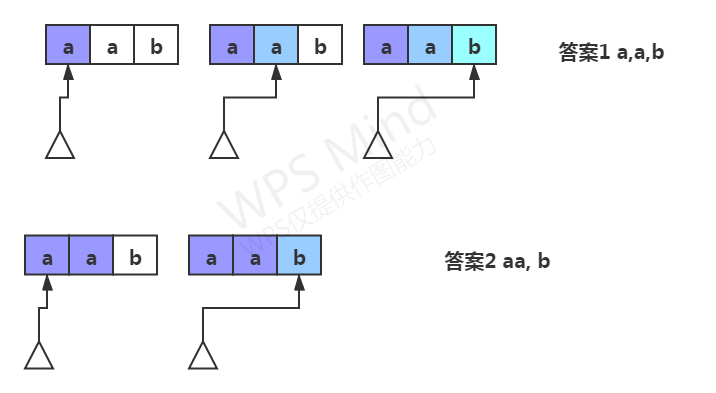
双指针判断是否是回文流程如下

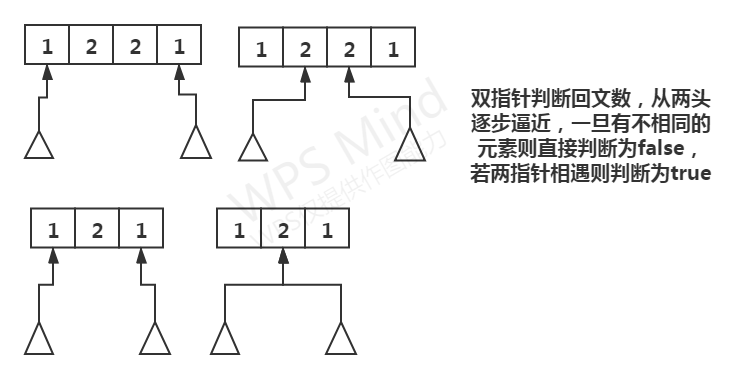
class Solution {
public:
    vector<vector<string>> ans;

    bool IsPalStr(const string& s) {
        int l = 0; int r = s.size() - 1;
        bool ret = true;
        while (l < r) {
            if (s[l] != s[r]) {ret = false; break;}
            l++; r--;
        }

        return ret;
    }

    void dfs(const string& s, int idx, vector<string>& v) {
        if (idx >= s.size()) {ans.push_back(v);return;}

        for (int len = 1; idx + len <= s.size(); len++) {
            string tmp = s.substr(idx, len);
            if (IsPalStr(tmp)) {
                v.push_back(tmp);
                dfs(s, idx + len, v);
                v.pop_back();
            }
        }

        return;
    }
    vector<vector<string>> partition(string s) {
        vector<string> v;
        dfs(s, 0, v);
        return ans;
    }
};

//===========================================

算法2 dp

dp
检查是否是回文的函数还可以再次优化，不必每次生成字串再去检测是否是回文。
可以直接使用dp[i][j]标记字符串下标i到j的子字符串是否是回文.

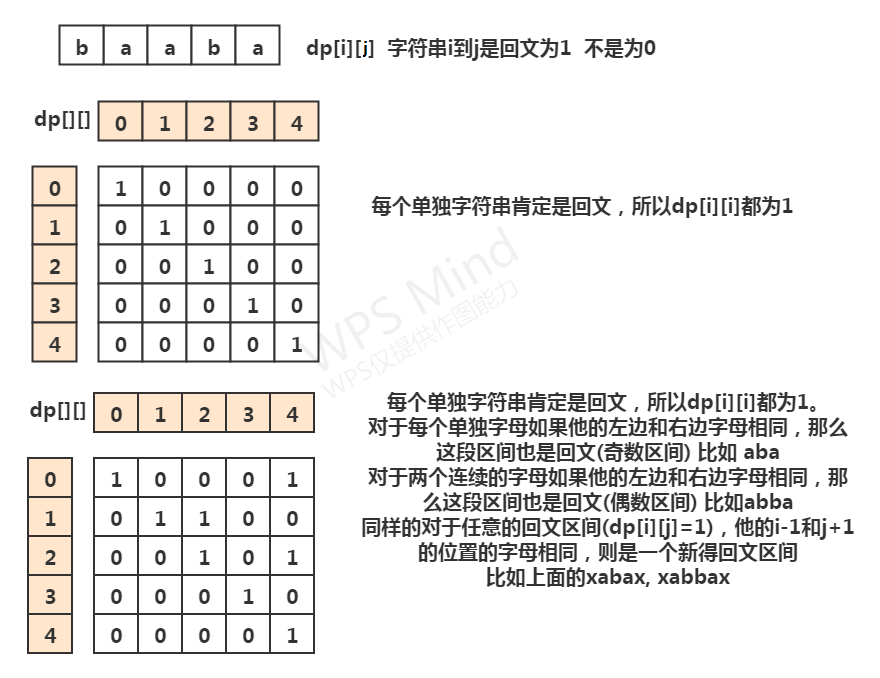
class Solution {
public:
    vector<vector<string>> ans;
    int dp[500][500];
    void initDp(const string& s)
    {
        memset(dp,0,sizeof(dp));

        for (int i = 0; i < s.size(); i++) {
            dp[i][i] = 1;
        }
        for (int i = 1; i < s.size(); i++) {
            int l = i - 1; int r = i + 1;
            while (l >= 0 && r < s.size() && s[l] == s[r]) {
                dp[l][r] = 1; l--; r++;
            }
            if (s[i] == s[i - 1]) {
                dp[i - 1][i] = 1;
                l = i - 2; r = i + 1;
                while (l >= 0 && r < s.size() && s[l] == s[r]) {
                    dp[l][r] = 1; l--; r++;
                }
            }
        }
    }void dfs(const string& s, int idx, vector<string>& v) {
        if (idx >= s.size()) {ans.push_back(v);return;}

        for (int len = 0; idx + len < s.size(); len++) {
            if (dp[idx][idx+len] == 1 ) {
                string tmp = s.substr(idx,len+1);
                v.push_back(tmp);
                dfs(s, idx + len+1, v);
                v.pop_back();
            }
        }

        return;
    }

    vector<vector<string>> partition(string s) {
        initDp(s);
        vector<string> v;
        dfs(s, 0, v);
        return ans;
    }
};