算法导论 红黑树 学习 插入(三) 图文

学习算法 还是建议看看算法导论

算法导论第三版 如果不看数学推导 仅看伪代码 难度还是适中

本系列只是记录我的学习心得 和伪代码转化代码的过程

深入学习 还是建议大家看看算法书籍 教程更加系统。

本文参考算法导论第13章节 红黑树

代码由本人写成

转载请标明出处

现在说插入元素

红黑树的插入跟二叉树的插入差不多 首先是查找合适的位置

插入 insert

注意 插入节点的颜色肯定是红色的

插入后由于有颜色的限制 要进行调整 insertfix

伪代码见 算法导论

代码和插入步骤图如下:

void RBInsert(std::shared_ptr<node>& root, std::shared_ptr<node> ins) {
	std::shared_ptr<node> y = nil;
	std::shared_ptr<node> x = root;

	while (x != nil) {
		y = x;
		if (ins->value_ < x->value_) {
			x = x->left_;
		}
		else {
			x = x->right_;
		}
	}
	ins->parent_ = y;
	if (y == nil) {
		root = ins;
	}
	else if (ins->value_ < y->value_) {
		y->left_ = ins;
	}
	else {
		y->right_ = ins;
	}
	ins->left_ = ins->right_ = nil;
	ins->color_ = red;
	// todo  fixup

	//RBInsertFixup(root, ins);
}

　　先不管插入后的颜色调整 来看看插入的步骤是怎么样的

　　代码如下

// rb.cpp : 定义控制台应用程序的入口点。
//

#include "stdafx.h"


// rbTreeTest2.cpp : 定义控制台应用程序的入口点。
//

#include "stdafx.h"
#include <memory>
#include <iostream>

using namespace std;

enum Color {
	red = 1,
	black
};

struct node {
	Color color_;
	std::shared_ptr<node> left_;
	std::shared_ptr<node> right_;
	std::shared_ptr<node> parent_;
	int value_;
	node() {
		left_ = right_ = parent_ = nullptr;
		value_ = -1;
		color_ = black;
	}
};

std::shared_ptr<node> nil(new node);


std::shared_ptr<node> CreateNode(Color color, int i) {
	std::shared_ptr<node> p(new node);
	p->color_ = color;
	p->left_ = nil;
	p->right_ = nil;
	p->parent_ = nil;
	p->value_ = i;
	return p;
}

void PrinTree(std::shared_ptr<node> root);


void RBInsert(std::shared_ptr<node>& root, std::shared_ptr<node> ins) {
	std::shared_ptr<node> y = nil;
	std::shared_ptr<node> x = root;

	while (x != nil) {
		y = x;
		if (ins->value_ < x->value_) {
			x = x->left_;
		}
		else {
			x = x->right_;
		}
	}
	ins->parent_ = y;
	if (y == nil) {
		root = ins;
	}
	else if (ins->value_ < y->value_) {
		y->left_ = ins;
	}
	else {
		y->right_ = ins;
	}
	ins->left_ = ins->right_ = nil;
	ins->color_ = red;
	// todo  fixup

	//RBInsertFixup(root, ins);
}

void PrinTree(std::shared_ptr<node> root) {
	if (root == nil) {
		return;
	}
	std::cout << root->value_ << " ";
	if (root->left_ != nil)
		PrinTree(root->left_);
	if (root->right_ != nil)
		PrinTree(root->right_);
}

int main()
{
	std::shared_ptr<node> root = CreateNode(black, 15);
	root->parent_ = nil;

	std::shared_ptr<node> x = root;
	std::shared_ptr<node> ins = CreateNode(black, 10);
	RBInsert(x, ins);
	
	ins = CreateNode(black, 20);
	RBInsert(x, ins);

	ins = CreateNode(black, 25);
	RBInsert(x, ins);

	ins = CreateNode(black, 12);
	RBInsert(x, ins);

	ins = CreateNode(black, 17);
	RBInsert(x, ins);


	PrinTree(root);
	std::cout << std::endl;


	return 0;
}

　　我们依次插入15 10 20 25 12 17

但是插入节点的时候，各个节点的颜色可能会破坏部分红黑树的性能

所以需要进行调节

分为三种情况

第一种情况

插入的红色节点Z 其父节点的兄弟节点即叔节点也是红色

那么将z节点的父节点和叔节点都改为黑色  z节点的父节点的父节点改为红色

Z节点设置为z节点的父节点的父节点 再次进行调整FIXUP

如图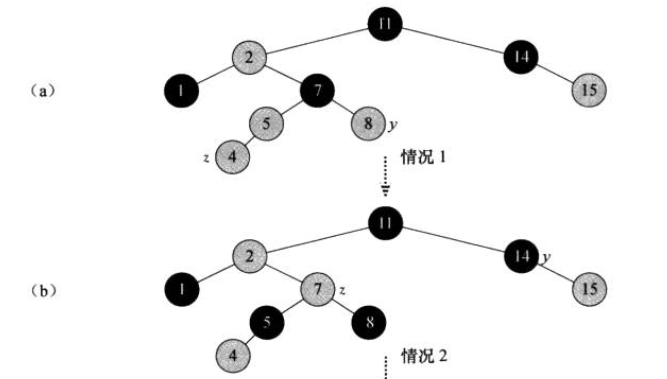

y是z的叔节点 红色 

那么 将 5号节点 、8号节点(y)改黑 7号改红 

z节点为7号节点 再次进行判断调整

第二种情况和第三种情况类似

z的叔节点y是黑色的 且z节点是右孩子

z的叔节点y是黑色的 且z节点是左孩子

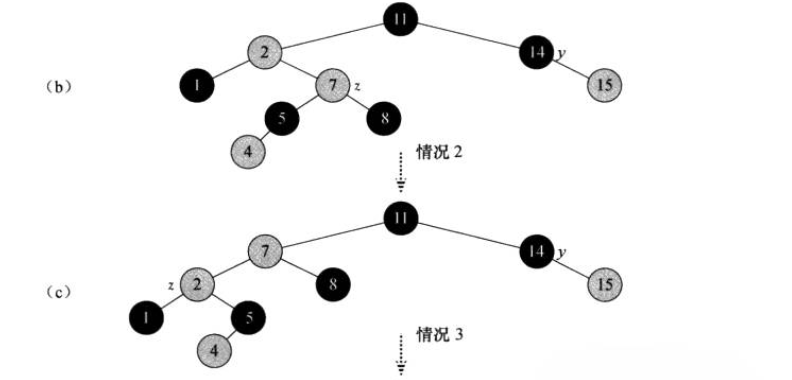
情况2和情况3 其实是通过一次旋转就可以转化了

实际操作中遇到情况2就将Z节点7号节点左旋转即可 转化为情况3

情况3再进行一次右旋转和颜色调整就可以达到平衡了

如图

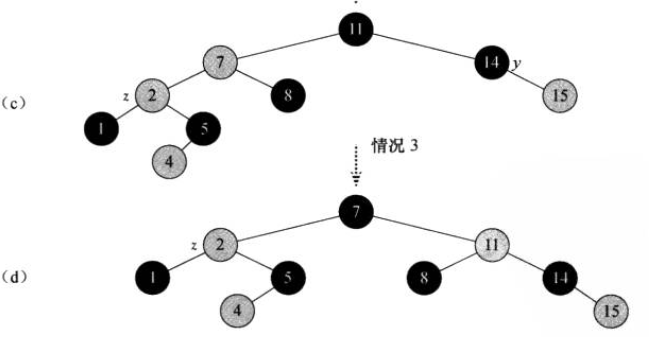
调整的伪代码和代码如下:

void RBInsertFixup(std::shared_ptr<node>& root, std::shared_ptr<node> z) {
	while (z->parent_->color_ == red) {	//插入节点Z是红色 若Z父节点也是红色则需要调整
		if (z->parent_ == z->parent_->parent_->left_){	// 父节点是左子树的情况
			std::shared_ptr<node> y = z->parent_->parent_->right_;
			if (y->color_ == red){					//	情况1
				z->parent_->color_ = black;
				y->color_ = black;
				z->parent_->parent_->color_ = red;
				z = z->parent_->parent_;
			}
			else {
				if (z == z->parent_->right_) {
					z = z->parent_;					//	情况2
					LeftRotate(root, z);
				}
				z->parent_->color_ = black;			//	情况3
				z->parent_->parent_->color_ = red;
				RightRotate(root, z->parent_->parent_);
			}
		}
		else {// 父节点是右子树的情况 与上面判断处理均是镜像对称
			std::shared_ptr<node> y = z->parent_->parent_->left_;
			if (y->color_ == red){
				z->parent_->color_ = black;
				y->color_ = black;
				z->parent_->parent_->color_ = red;
				z = z->parent_->parent_;
			}
			else {
				if (z == z->parent_->left_) {
					z = z->parent_;
					RightRotate(root, z);
				}
				z->parent_->color_ = black;
				z->parent_->parent_->color_ = red;
				LeftRotate(root, z->parent_->parent_);
			}
		}	
	}//while (z->parent_->color_ == red)
	root->color_ = black;
}//function end

下面是全部代码

// rbTreeTest.cpp : 定义控制台应用程序的入口点。
//

#include "stdafx.h"
#include <memory>
#include <iostream>

using namespace std;

enum Color {
	red = 1,
	black
};

struct node {
	Color color_;
	std::shared_ptr<node> left_;
	std::shared_ptr<node> right_;
	std::shared_ptr<node> parent_;
	int value_;
	node() {
		left_ = right_ = parent_ = nullptr;
		value_ = -1;
		color_ = black;
	}
};

std::shared_ptr<node> nil(new node);


std::shared_ptr<node> CreateNode(Color color, int i) {
	std::shared_ptr<node> p(new node);
	p->color_ = color;
	p->left_ = nil;
	p->right_ = nil;
	p->parent_ = nil;
	p->value_ = i;
	return p;
}

void RightRotate(std::shared_ptr<node>& root, std::shared_ptr<node> x) {
	std::shared_ptr<node> y = x->left_;
	x->left_ = y->right_;
	if (y->right_ != nil)
		y->right_->parent_ = x;
	y->parent_ = x->parent_;
	if (x->parent_ == nil) {
		root = y;
	}
	else if (x->parent_->left_ == x) {
		x->parent_->left_ = y;
	}
	else {
		x->parent_->right_ = y;
	}

	y->right_ = x;
	x->parent_ = y;
}

void LeftRotate(std::shared_ptr<node>& root, std::shared_ptr<node> x) {
	std::shared_ptr<node> y = x->right_;
	x->right_ = y->left_;
	if (y->left_ != nil)
		y->left_->parent_ = x;

	y->parent_ = x->parent_;
	if (x->parent_ == nil) {
		root = y;
	}
	else if (x->parent_->left_ == x) {
		x->parent_->left_ = y;
	}
	else {
		x->parent_->right_ = y;
	}
	y->left_ = x;
	x->parent_ = y;
}

void PrinTree(std::shared_ptr<node> root) {
	if (root == nil) {
		std::cout << "nil:" << ":color-" << root->color_ << " ; " << std::endl << std::endl;
		return;
	}
	std::cout << root->value_ << ":color-" << root->color_ << "; address:" << root << std::endl;
	if (root->parent_ == nil) {
		std::cout << "parent_:" << "nil" << std::endl;
	}
	else {
		std::cout << "parent_:" << root->parent_ << std::endl;
	}

	if (root->left_ == nil) {
		std::cout << "left_:" << "nil" << std::endl;
	}
	else {
		std::cout << "left_:" << root->left_ << std::endl;
	}


	if (root->right_ == nil) {
		std::cout << "right_:" << "nil" << std::endl;
	}
	else {
		std::cout << "right_:" << root->right_ << std::endl;
	}

	std::cout << std::endl;


	if (root->left_ != nil)
		PrinTree(root->left_);
	if (root->right_ != nil)
		PrinTree(root->right_);
}

void RBInsertFixup(std::shared_ptr<node>& root, std::shared_ptr<node> z) {
	while (z->parent_->color_ == red) {   //插入节点Z是红色 若Z父节点也是红色则需要调整
		if (z->parent_ == z->parent_->parent_->left_) {  // 父节点是左子树的情况
			std::shared_ptr<node> y = z->parent_->parent_->right_;
			if (y->color_ == red) {                   //  情况1
				z->parent_->color_ = black;
				y->color_ = black;
				z->parent_->parent_->color_ = red;
				z = z->parent_->parent_;
			}
			else {
				if (z == z->parent_->right_) {
					z = z->parent_;                  //  情况2
					LeftRotate(root, z);
				}
				z->parent_->color_ = black;           //  情况3
				z->parent_->parent_->color_ = red;
				RightRotate(root, z->parent_->parent_);
			}
		}
		else {// 父节点是右子树的情况 与上面判断处理均是镜像对称
			std::shared_ptr<node> y = z->parent_->parent_->left_;
			if (y->color_ == red) {
				z->parent_->color_ = black;
				y->color_ = black;
				z->parent_->parent_->color_ = red;
				z = z->parent_->parent_;
			}
			else {
				if (z == z->parent_->left_) {
					z = z->parent_;
					RightRotate(root, z);
				}
				z->parent_->color_ = black;
				z->parent_->parent_->color_ = red;
				LeftRotate(root, z->parent_->parent_);
			}
		}
	}//while (z->parent_->color_ == red)
	root->color_ = black;
}//function end

void RBInsert(std::shared_ptr<node>& root, std::shared_ptr<node> ins) {
	std::shared_ptr<node> y = nil;
	std::shared_ptr<node> x = root;

	while (x != nil) {
		y = x;
		if (ins->value_ < x->value_) {
			x = x->left_;
		}
		else {
			x = x->right_;
		}
	}
	ins->parent_ = y;
	if (y == nil) {
		root = ins;
	}
	else if (ins->value_ < y->value_) {
		y->left_ = ins;
	}
	else {
		y->right_ = ins;
	}
	ins->left_ = ins->right_ = nil;
	ins->color_ = red;
	// todo  fixup
	RBInsertFixup(root,ins);
}

void TestInsert() {
	std::shared_ptr<node> root = nil;
	std::shared_ptr<node> x = CreateNode(red, 7);
	RBInsert(root, x);


	x = CreateNode(red, 4);
	RBInsert(root, x);

	x = CreateNode(red, 11);
	RBInsert(root, x);

	x = CreateNode(red, 3);
	RBInsert(root, x);

	x = CreateNode(red, 6);
	RBInsert(root, x);

	x = CreateNode(red, 9);
	RBInsert(root, x);

	x = CreateNode(red, 18);
	RBInsert(root, x);

	x = CreateNode(red, 2);
	RBInsert(root, x);

	x = CreateNode(red, 14);
	RBInsert(root, x);

	x = CreateNode(red, 19);
	RBInsert(root, x);

	x = CreateNode(red, 12);
	RBInsert(root, x);

	x = CreateNode(red, 17);
	RBInsert(root, x);

	x = CreateNode(red, 22);
	RBInsert(root, x);

	x = CreateNode(red, 20);
	RBInsert(root, x);
	PrinTree(root);
	std::cout << std::endl;
}

int main()
{
	TestInsert();

	return 0;
}