数据结构简介
3.1 数据结构介绍
数据结构 : 数据用什么样的方式组合在一起。就是数据的存储方式。
3.2 常见数据结构
数据存储的常用结构有:栈、队列、数组、链表和红黑树。我们分别来了解一下:
3.2.1栈和队列
栈
- 栈:stack,又称堆栈,它是运算受限的线性表,其限制是仅允许一端进行插入和删除操作,不允许在其他任何位置进行添加、查找、删除等操作。
简单的说:采用该结构的集合,对元素的存取有如下的特点
- 先进后出(即,存进去的元素,要在后它后面的元素依次取出后,才能取出该元素)。例如,子弹压进弹夹,先压进去的子弹在下面,后压进去的子弹在上面,当开枪时,先弹出上面的子弹,然后才能弹出下面的子弹。
- 栈的入口、出口的都是栈的顶端位置。
- 需求:演示向栈中存储数据ABC,然后再取出数据的过程。
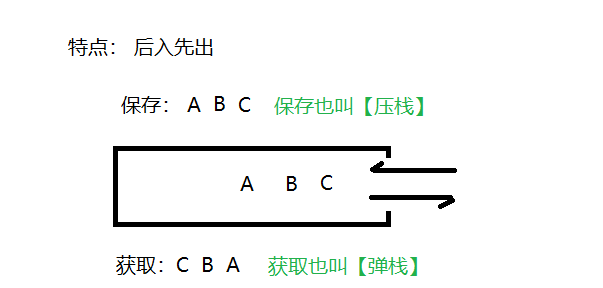
这里两个名词需要注意:
- 压栈:就是存元素。即,把元素存储到栈的顶端位置,栈中已有元素依次向栈底方向移动一个位置。
- 弹栈:就是取元素。即,把栈的顶端位置元素取出,栈中已有元素依次向栈顶方向移动一个位置。
队列
-
队列:queue,简称队,它同堆栈一样,也是一种运算受限的线性表,其限制是仅允许在一端进行插入,而在另一端进行取出并删除。
简单的说,采用该结构的集合,对元素的存取有如下的特点:
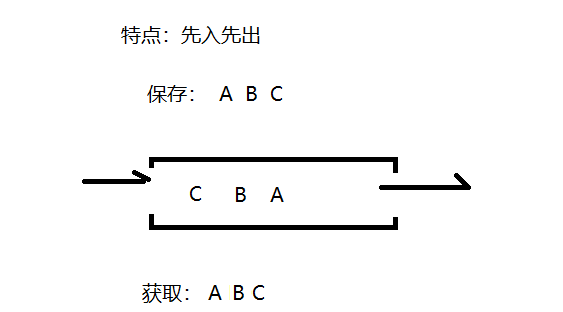
- 先进先出(即,存进去的元素,要在后它前面的元素依次取出后,才能取出该元素)。例如,小火车过山洞,车头先进去,车尾后进去;车头先出来,车尾后出来。排队买票等。
- 队列的入口、出口各占一侧。例如,下图中的左侧为入口,右侧为出口。
- 需求:演示向队列中存储数据ABC,然后再取出数据的过程。
3.2.2数组和链表
数组
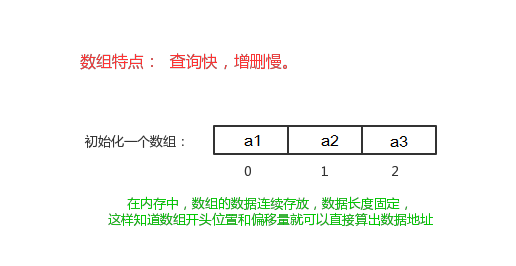
是有序的元素序列,数组是在内存中开辟一段连续的空间,并在此空间存放元素.就像是一排出租屋,有100个房间,从001到100每个房间都有固定编号,通过编号就可以快速找到租房子的人。
简单的说,采用该结构的集合,对元素的存取有如下的特点:
-
特点:查找快,增删慢

-
查找元素快:通过索引,可以快速访问指定位置的元素
-
增删元素慢
-
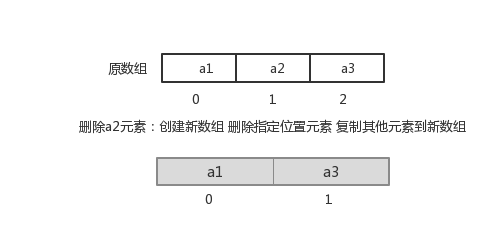
指定索引位置增加元素:需要创建一个新数组,将指定新元素存储在指定索引位置,再把原数组元素根据索引,复制到新数组对应索引的位置。如下图

-
指定索引位置删除元素:需要创建一个新数组,把原数组元素根据索引,复制到新数组对应索引的位置,原数组中指定索引位置元素不复制到新数组中。如下图![]
链表
- 链表:linked list,由一系列结点node(链表中每一个元素称为结点)组成,结点可以在运行时动态生成。每个结点包括多个部分:一部分是存储数据元素的数据域,另一部分是存储前后一个结点地址的指针域。我们常说的链表结构有单向链表与双向链表,那么这里给大家介绍的是单向链表。后面讲双向链表。


简单的说,采用该结构的集合,对元素的存取有如下的特点:
-
多个结点之间,通过地址进行连接。例如,多个人手拉手,每个人使用自己的右手拉住下个人的左手,依次类推,这样多个人就连在一起了。
-
查找元素慢:想查找某个元素,需要通过连接的节点,依次向后查找指定元素。
- 增删元素快:

说明:
查找慢:因为每个元素在内存中位置不同,所以查找慢。
增删快:增删时只需要改变前后两个元素的指针指向,对其他元素没有任何影响。
3.2.3 树基本结构介绍
树结构
计算机中的树结构就是生活中倒立的树。
树具有的特点:
- 每一个节点有零个或者多个子节点
- 没有父节点的节点称之为根节点,一个树最多有一个根节点。类似于生活中大树的树根。
- 每一个非根节点有且只有一个父节点

| 名词 | 含义 |
|---|---|
| 节点 | 指树中的一个元素(数据) |
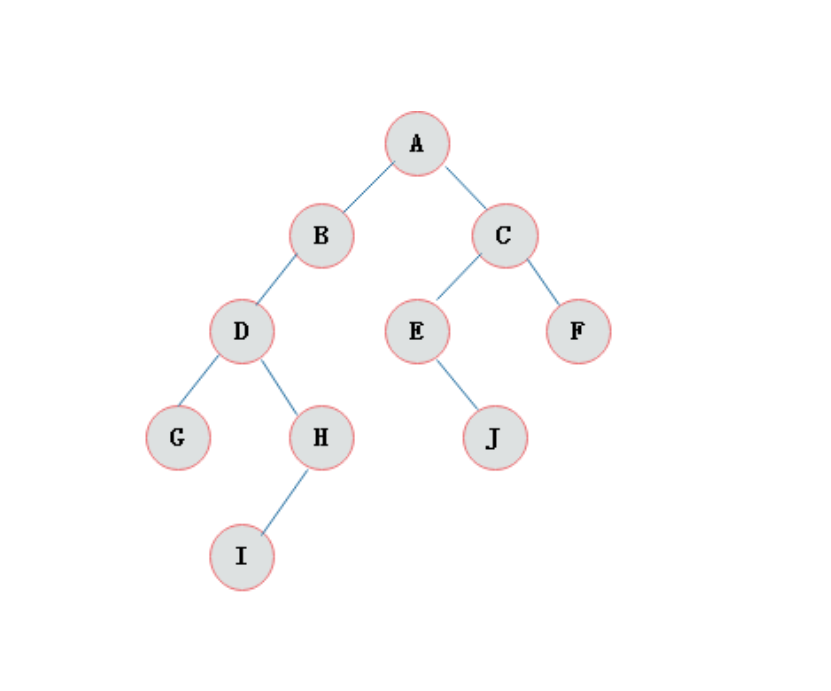
| 节点的度 | 节点拥有的子树(儿子节点)的个数,二叉树的度不大于2,例如:下面二叉树A节点的度是2,E节点的度是1,F节点的度是0 |
| 叶子节点 | 度为0的节点,也称之为终端结点,就是没有儿子的节点。 |
| 高度 | 叶子结点的高度为1,叶子结点的父节点高度为2,以此类推,根节点的高度最高。例如下面二叉树ACF的高度是3,ACEJ的高度是4,ABDHI的高度是5. |
| 层 | 根节点在第一层,以此类推 |
| 父节点 | 若一个节点含有子节点,则这个节点称之为其子节点的父节点 |
| 子节点 | 子节点是父节点的下一层节点 |
| 兄弟节点 | 拥有共同父节点的节点互称为兄弟节点 |
二叉树
如果树中的每个节点的子节点的个数不超过2,那么该树就是一个二叉树。
二叉查找树
上面都是关于树结构的一些概念,那么下面的二叉查找树就是和java有关系的了,那么接下来我们就开始学习下什么是二叉查找树。
二叉查找树的特点:
1. 【左子树】上所有的节点的值均【小于】他的【根节点】的值
2. 【右子树】上所有的节点值均【大于】他的【根节点】的值
3. 每一个子节点最多有两个子树
4. 二叉查找树中没有相同的元素
说明:
1.左子树:根节点左边的部分称为左子树.
2.右子树: 根节点右边的部分称为右子树.
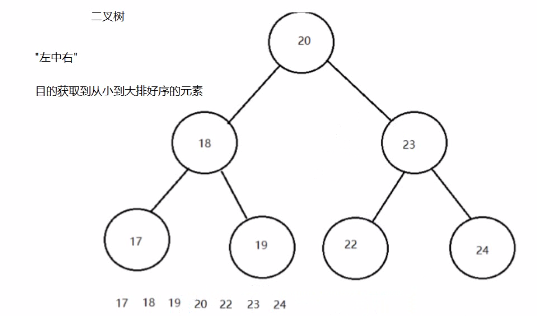
案例演示(20,18,23,22,17,24,19)数据的存储过程;

遍历二叉树有几种遍历方式:
1)前序(根)遍历:根-----左子树-----右子树
2)中序(根)遍历:左子树-----根-----右子树
3)后序(根)遍历:左子树-----右子树-----根
4)按层遍历:从上往下,从左向右
遍历获取元素的时候可以按照"左中右"(中序(根)遍历)的顺序进行遍历来实现数据的从小到大排序;
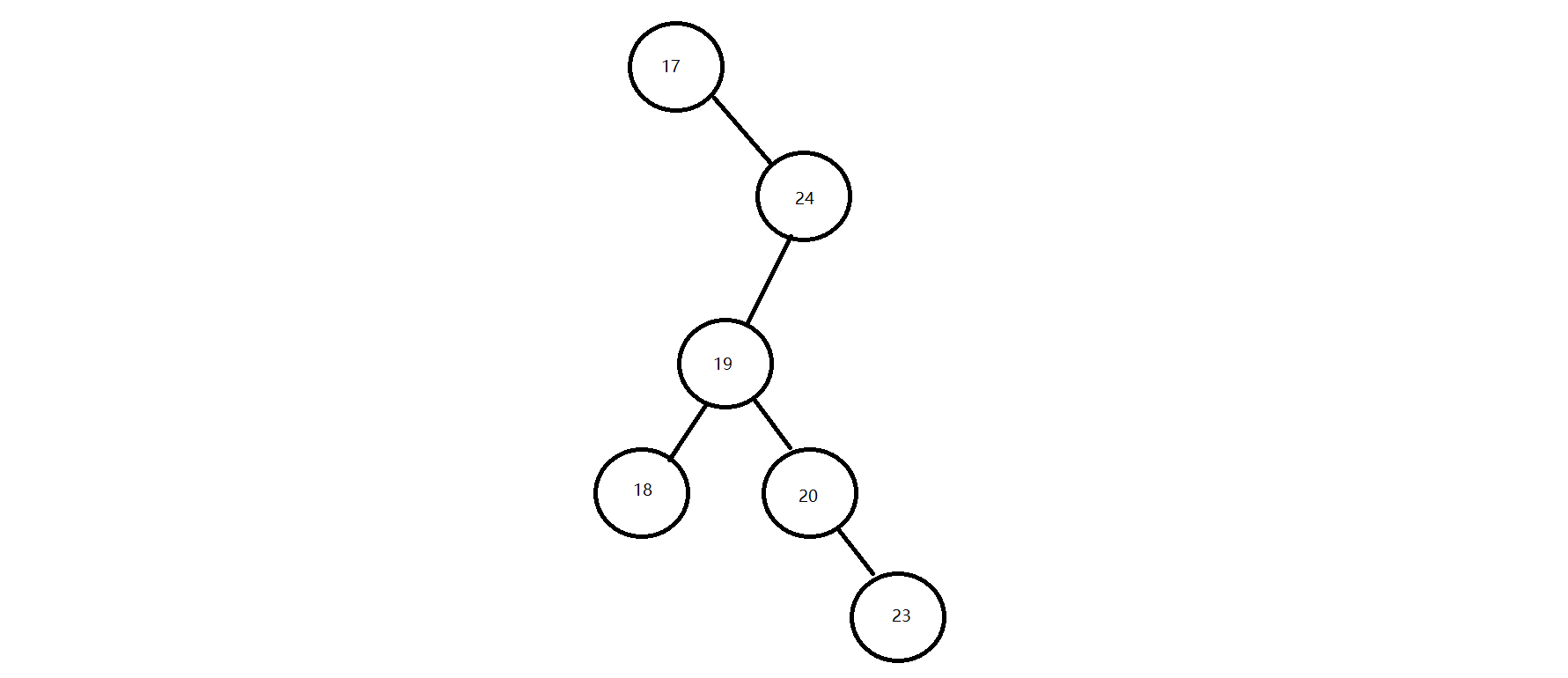
注意:二叉查找树存在的问题:会出现"瘸子"的现象,影响查询效率
(17,24,19,18,20,23)数据的存储过程;
平衡二叉树
概述
为了避免出现"瘸子"的现象,减少树的高度,提高我们的搜素效率,又存在一种树的结构:"平衡二叉树"
规则:它的左右两个子树的高度差的绝对值不超过1(小于等于1),并且左右两个子树都是一棵平衡二叉树
如下图所示:
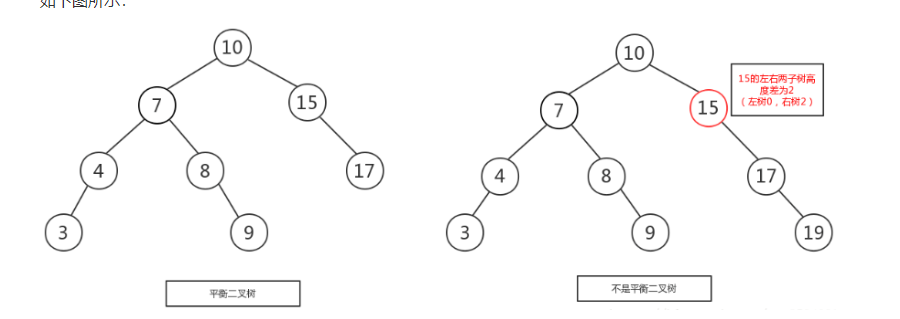
1.如上图所示,左图是一棵平衡二叉树.
举例:
1)根节点10,左右两子树的高度差的绝对值是1。10的左子树有3个子节点(743),10的右子树有2个子节点.所 以高度差是1.
2)15的左子树没有节点,右子树有一个子节点(17),两个子树的高度差的绝对值是1.
2.而右图不是一个平衡二叉树,虽然根节点10左右两子树高度差是0(左右子树都是3个子节点),但是右子树15的左右子树高度差为2,不符合定义。15的左子树的子节点为0,右子树的子节点为2.差的绝对值是2。所以右图不是一棵平衡二叉树。
说明:为什么需要平衡二叉树?如下图:
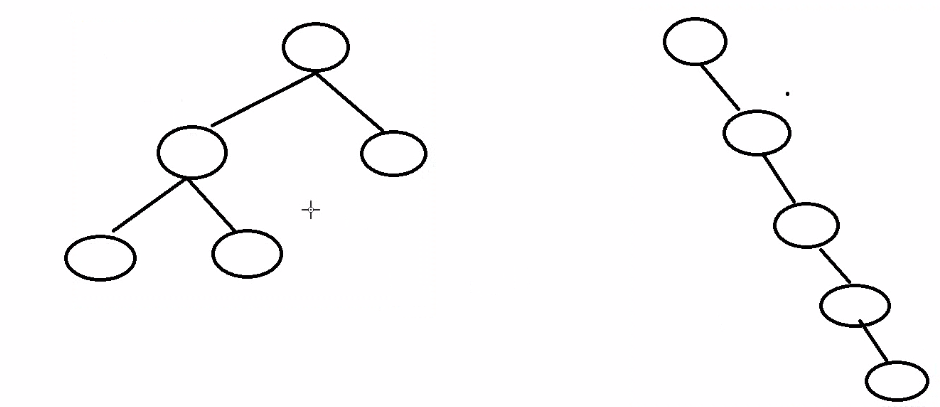
左图是一个平衡二叉树,如果查到左子树的叶子节点需要执行3次。而右图不是一个平衡二叉树,那么查到最下面的叶子节点需要执行5次,相对来说平衡二叉树查找效率更高。
旋转
在构建一棵平衡二叉树的过程中,当有新的节点要插入时,检查是否因插入后而破坏了树的平衡,如果是,则需要做旋转去改变树的结构,变为平衡的二叉树。
各种情况如何旋转:
左左:只需要做一次【右旋】就变成了平衡二叉树。
右右:只需要做一次【左旋】就变成了平衡二叉树。
左右:先做一次分支的【左旋】,再做一次树的【右旋】,才能变成平衡二叉树。
右左:先做一次分支的【右旋】,再做一次数的【左旋】,才能变成平衡二叉树。
课上只讲解“左左”的情况,其余情况都作为扩展去学习,这里只是让你知道怎么旋转即可。
左左
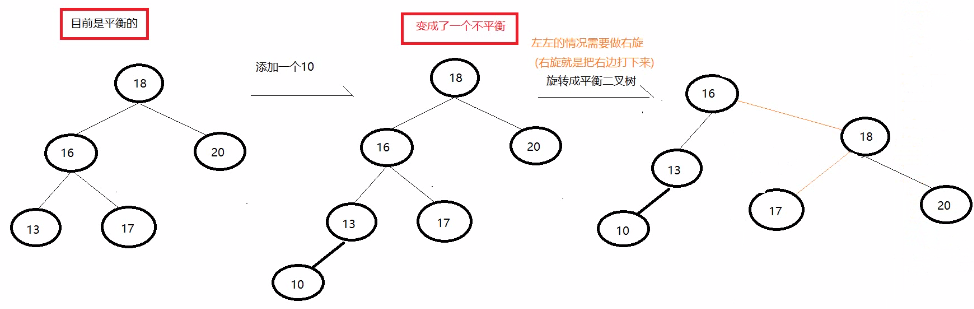
左左即为在原来平衡的二叉树上,在节点的左子树的左子树下,有新节点插入,导致节点的左右子树的高度差为2,如下即为"18"节点的左子树"16",的左子树"13",插入了节点"10"导致失衡。
需求:二叉树已经存在的数据:18 16 20 13 17
后添加的数据是:10
说明:
1.左左:只需要做一次右旋就变成了平衡二叉树。
2.右旋:将节点的左支往右拉,左子节点变成了父节点,并把晋升之后多余的右子节点出让给降级节点的左子节点
红黑树
概述
红黑树是一种自平衡的二叉查找树,是计算机科学中用到的一种数据结构,它是在1972年由Rudolf Bayer发明的,当时被称之为平衡二叉B树,后来,在1978年被Leoj.Guibas和Robert Sedgewick修改为如今的"红黑树"。它是一种特殊的二叉查找树,红黑树的每一个节点上都有存储位表示节点的颜色,可以是红或者黑;
红黑树不是高度平衡的,它的平衡是通过"红黑树的特性"进行实现的;
红黑树的特性:
1. 每一个节点或是红色的,或者是黑色的。
2. 根节点必须是黑色
3. 每个叶节点(Nil)是黑色的;(如果一个节点没有子节点,则该节点相应的指针属性值为Nil,这些 Nil视为叶节点)
4. 如果某一个节点是红色,那么它的子节点必须是黑色(不能出现两个红色节点相连的情况)
5. 对每一个节点,从该节点到其所有后代叶节点的路径上,均包含相同数目的黑色节点
如下图所示就是一个红黑树
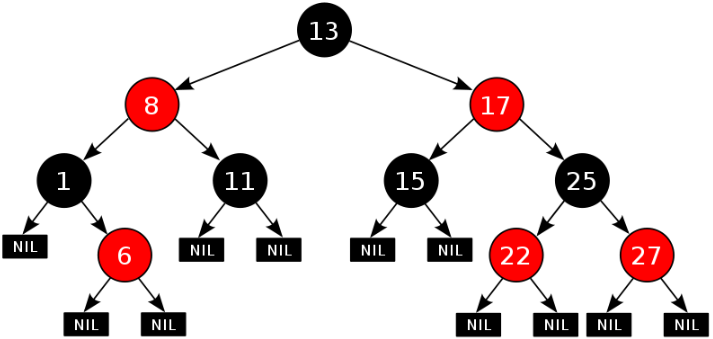
在进行元素插入的时候,和之前一样; 每一次插入完毕以后,使用红黑规则进行校验,如果不满足红黑规则,就需要通过变色,左旋和右旋来调整树,使其满足红黑规则;