目录
什么是k近邻算法
模型的三个基本要素
构造kd树
kd树的最近邻搜索
kd树的k近邻搜索
Python代码(sklearn库)
|
什么是K近邻算法(k-Nearest Neighbor,kNN) |
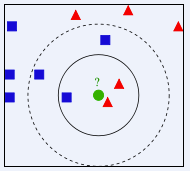
引例
假设有数据集,其中前6部是训练集(有属性值和标记),我们根据训练集训练一个KNN模型,预测最后一部影片的电影类型。

首先,将训练集中的所有样例画入坐标系,也将待测样例画入

然后计算待测分类的电影与所有已知分类的电影的欧式距离

接着,将这些电影按照距离升序排序,取前k个电影,假设k=3,那么我们得到的电影依次是《He's Not Really Into Dudes》、《Beautiful Woman》和《California Man》。而这三部电影全是爱情片,因此我们判定未知电影是爱情片。
百度百科定义
邻近算法,或者说K最近邻(kNN,k-NearestNeighbor)分类算法是数据挖掘分类技术中最简单的方法之一。所谓K最近邻,就是k个最近的邻居的意思,说的是每个样本都可以用它最接近的k个邻居来代表。
kNN算法的核心思想是如果一个样本在特征空间中的k个最相邻的样本中的大多数属于某一个类别,则该样本也属于这个类别,并具有这个类别上样本的特性。该方法在确定分类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。 kNN方法在类别决策时,只与极少量的相邻样本有关。由于kNN方法主要靠周围有限的邻近的样本,而不是靠判别类域的方法来确定所属类别的,因此对于类域的交叉或重叠较多的待分样本集来说,kNN方法较其他方法更为适合。
|
模型的三个基本要素 |
kNN模型的三个基本要素:(1)距离度量、(2)k值的选择、(3)分类决策规则。接下来,我们一一介绍这三要素。
(1)距离度量
在引例中所画的坐标系,可以叫做特征空间。特征空间中两个实例点的距离是两个实例点相似程度的反应(距离越近,相似度越高)。kNN模型使用的距离一般是欧氏距离,但也可以是其他距离如:曼哈顿距离
(2)k值的选择
k值的选择会对kNN模型的结果产生重大影响。选择较大的k值,相当于用较大邻域中的训练实例进行预测,模型会考虑过多的邻近点实例点,甚至会考虑到大量已经对预测结果没有影响的实例点,会让预测出错;选择较小的k值,相当于用较小邻域中的训练实例进行预测,会使模型变得敏感(如果邻近的实例点恰巧是噪声,预测就会出错)。
在应用中,k值一般取一个比较小的数值。通常采用交叉验证法来选取最优的k值。
(3)分类决策规则
kNN中的分类决策规则往往是多数表决,即由输入实例的k个邻近的训练实例中的多数类决定待测实例的类。
|
构造kd树 |
k近邻法最简单的实现方式是线性扫描,需要计算待测实例与每个实例的距离,在大数据上不可行。为了提高k近邻搜索效率,考虑使用特殊的结构存储训练数据,以减少计算距离的次数,可以使用kd树(kd tree)方法。kd树分为两个过程——构造kd树(使用特殊结构存储训练集)、搜索kd树(减少搜索计算量)。
下面用一个例子演示构造kd树的过程:
给定一个二维空间的数据集(含有标记的一般叫训练集,不含标记的一般叫数据集): ,请画出:特征空间的划分过程、kd树的构造过程。
,请画出:特征空间的划分过程、kd树的构造过程。
第一步:
选择x(1)轴,6个数据点的x(1)坐标上的数字分别是2,5,9,4,8,7。取中位数7(这里不是严格意义的中位数,默认取较大的数),以x(1)=7将特征空间分为两个矩形:
特征空间: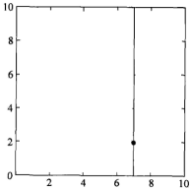 kd树:
kd树: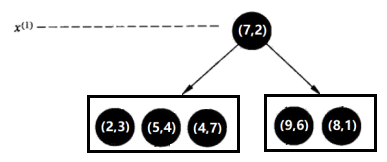
第二步:
选择x(2)轴,处理左子树,3个数据点的x(2)坐标上的数字分别是3,4,7。取中位数4,以x(2)=4将左子树对应的特征空间分为两个矩形;处理右子树,2个数据点的x(2)坐标上的数字分别是6,1。取中位数6(这里不是严格意义的中位数,默认取较大的数),以x(2)=6将右子树对应的特征空间分为两个矩形:
特征空间: kd树:
kd树: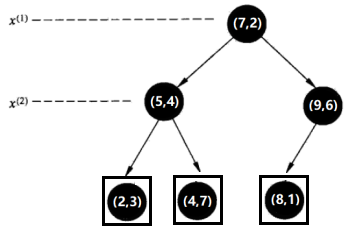
第三步:
选择x(循环数%特征数+1)轴,即x(3%2+1),即x(1)轴,分别处理所有待处理的节点:
特征空间: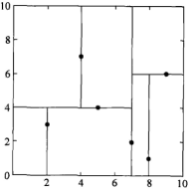 kd树:
kd树: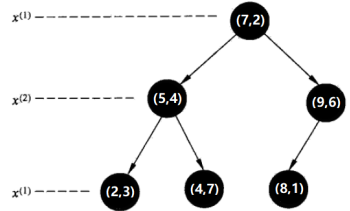
|
kd树的最近邻搜索 |
假设要对待测样本点(2,4.5)进行类别预测,那么就要在kd树里搜索它的k个邻居,然后投票决定其类别。
先介绍:kd树的最近邻搜索(k=1)。即,已构造的kd树、目标点x(2,4.5);输出:x的最近邻。
第一步:
在kd树中找出包含目标点x的叶结点:从根结点出发,递归地向下访问kd树。若目标点x当前维的坐标小于切分点的坐标,则移动到左子结点,否则移动到右子结点。直到子结点为叶结点为止。由于2<7,进入左子树;4.5>4,进入右子树,因此当前到达的叶节点是(4,7)。
第二步:
先将以此叶结点(4,7)定为“当前最近点”。

第三步:
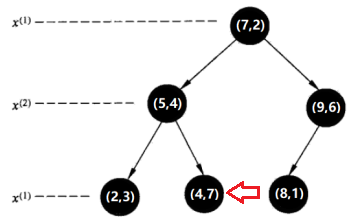
回退到(5,4),如果该结点(5,4)保存的实例点比当前最近点距离目标点更近,则以该实例点为“当前最近点”。计算发现确实(5,4)距(2,4.5)更近,因此将(5,4)定为“当前最近点”,将节点(5,4)到待测点的距离设为L(5,4)。

第四步:
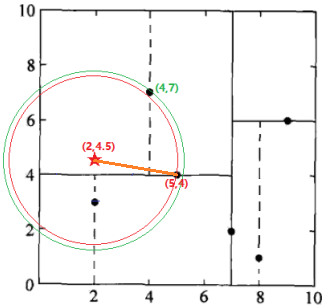
检查(5,4)的另一子节点(2,3)对应的区域是否与以待测点为球心、以待测点与“当前最近点”间的距离为半径的超球体(红色圆圈)相交(这里是相交的)。
如果不相交:向上回退到(7,2),转入第三步。
如果相交:可能在(2,3)结点对应的区域内存在距目标点更近的点,移动到(2,3)结点。接着,递归地进行最近邻搜索(执行结果:节点(2,3)是到待测点的距离是最近的,将这个距离设为L(2,3)),接着比较L(2,3) < L(5,4),因此,将(2,3)定为“当前最近点”,向上回退到(7,2),转入第三步。

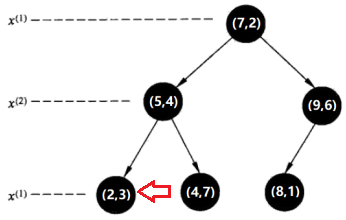
第五步(其实是第三步,这里是为了将搜索过程演示完毕):
回退到(7,2),如果该结点(7,2)保存的实例点比当前最近点距离目标点更近,则以该实例点为“当前最近点”。计算发现(7,2)距(2,4.5)更远,因此,无需更新“当前最近点”。
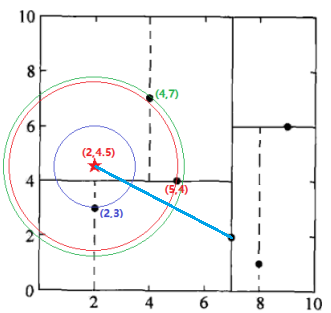
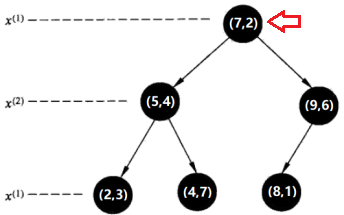
第六步(其实是第四步,这里是为了将搜索过程演示完毕):
检查(7,2)的另一子节点(9,6)对应的区域是否与以待测点为球心、以待测点与“当前最近点”间的距离为半径的超球体(蓝色圆圈)相交(这里是不相交的)。
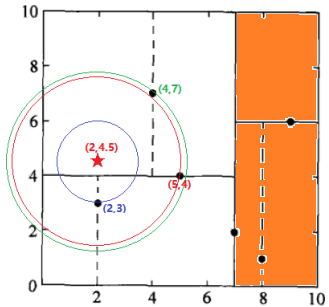
如果不相交:向上回退,发现已经是根节点了,无法回退,程序停止,最终得到的最近邻节点是(2,3)。
二娃:看你啰嗦了半天,kd树的搜索,究竟是如何减少搜索计算量的呢?
其实,主要减少计算量的步骤在于:判断超球体与某点对应区域是否相交。如果不相交,那就直接舍弃对那个节点及其子节点的搜索。
|
kd树的k近邻搜索 |
我们知道最近邻搜索(k=1)中,我们首先存储一个我们自认为是“当前最近点”的节点,然后在搜索过程中,找到更近的就替换掉。
其实这种思想在k近邻搜索(k>1)中同样适用,即,我们首先存储k个我们自认为是“当前最近点”的节点集合,然后在搜索过程中,找到比集合中任何一个更近的,就取代集合中距离待测点位置最远的节点。
|
Python代码(sklearn库) |
# -*- coding: utf-8 -*- import numpy as np from sklearn.datasets import load_iris from sklearn import neighbors iris = load_iris() trainX = iris.data trainY = iris.target clf=neighbors.KNeighborsClassifier(n_neighbors=6, weights='uniform', algorithm='auto', leaf_size=30, p=2, metric='minkowski', metric_params=None, n_jobs=1) ''' @param n_neighbors: 指定kNN的k值 @param weights: 'uniform': 本节点的所有邻居节点的投票权重都相等 'distance': 本节点的所有邻居节点的投票权重与距离成反比 @param algorithm: 惩罚项系数的倒数,越大,正则化项越小 'ball_tree': BallTree算法 'kd_tree': kd树算法 'brute': 暴力搜索算法 'auto': 自动决定适合的算法 @param leaf_size: 指定ball_tree或kd_tree的叶节点规模。他影响树的构建和查询速度 @param p: p=1:曼哈顿距离; p=2:欧式距离 @param metric: 指定距离度量,默认为'minkowski'距离 @param n_jobs: 任务并行时指定使用的CPU数,-1表示使用所有可用的CPU @method fit(X,y): 训练模型 @method predict(X): 预测 @method score(X,y): 计算在(X,y)上的预测的准确率 @method predict_proba(X): 返回X预测为各类别的概率 @method kneighbors(X, n_neighbors, return_distance): 返回样本点的k近邻点。如果return_distance=True,则也会返回这些点的距离 @method kneighbors_graph(X, n_neighbors, mode): 返回样本点的连接图 ''' clf.fit(trainX,trainY) print "训练准确率:" + str(clf.score(trainX,trainY)) print "测试准确率:" + str(clf.score(trainX,trainY)) ''' 训练准确率:0.973333333333 测试准确率:0.973333333333 '''