1、介绍
Logistic回归主要用于二分类。属于监督学习算法的一种。
2、过程
1)logistic sigmoid函数
其具体公式为:
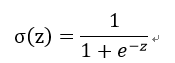
下图给出了其图像:
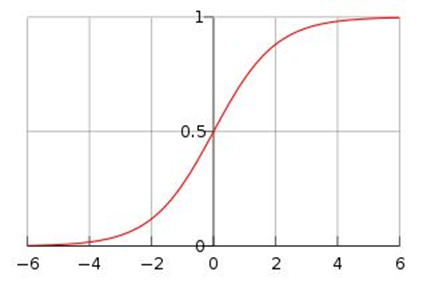
当x为0时,其函数值为0.5,随着x的增大,对应的函数值会逼近于1;随着x的减少,其值会趋于0.当横坐标刻度足够大时,其看上去会像一个阶跃函数。
采用该函数进行回归时,可以在每个特征上乘以一个回归系数,然后把结果相加,总和代入函数中,当函数值大于0.5的被分为1类,否则分为0类。
那么,怎么确定回归系数呢?
假设一个数据含有n个特征值,记为x1,x2,…,xn,对应的回归系数记为w1,w2,w3,…,wn,那么我们可以以矩阵(向量)的形式来表示:
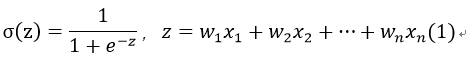
其中:
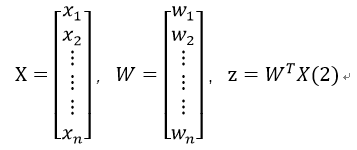
现在我们需要确定W列向量中每个变量的值。
假设有P0和P1两个条件概率:
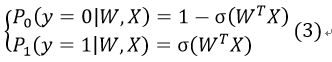
P0表示在当前W、X的情况下,函数值(我们记为y)为0,即当前数据被分到0类的概率,P1表示被分到1类的概率。
因此我们得到概率函数为:
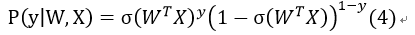
该函数是指,y为1时,就只考虑其为1的概率;y为0时,只考虑为0的概率。我们需要找到合适的W,然后最大化这个概率,尽可能使其分类正确。
2)最佳回归系数确定--基于最优化方法
假定样本与样本之间相互独立,那么整个样本集分类正确的概率即为所有样本分类正确的概率的乘积(似然估计函数),这里我们设总样本数目为m:
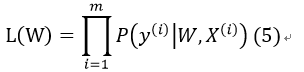
其中,y(i)表示第i个样本的分类,X(i)为第i个样本的特征向量。将式(4)代入式(5),得:
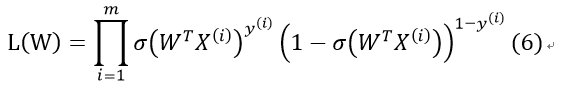
我们通过对该算式取对数ln()进行简化(对数似然函数):
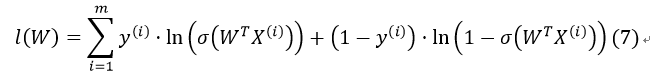
满足该函数最大的W即为我们所要求解的值(最大似然估计值)。
梯度上升法
我们通过用梯度上升法来求其局部极大值(也可以取负对数采用梯度下降法)。即让参数W沿着该函数梯度上升的方向变化:

其中,α为步长,即表示向梯度上升方向移动的距离。
对于函数σ(z),其对z的导数为:
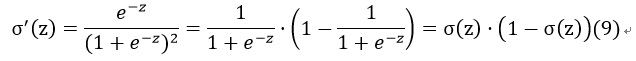
接下来,我们对l(W)求偏导:
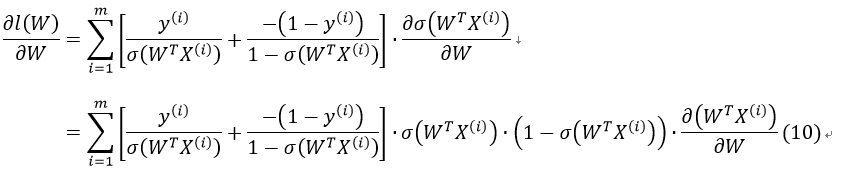
由于:

所以有:
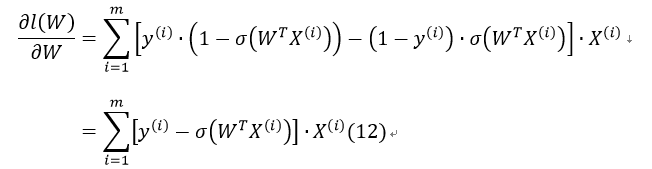
因此,最后梯度上升的迭代公式为:
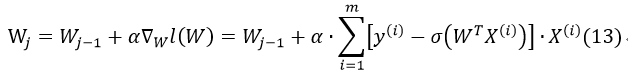
如果把m个样例的特征及其正确分类按行排成矩阵:
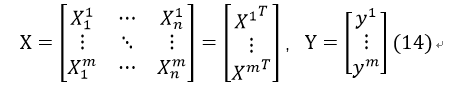
其中第i行表示第i个样例的n个特征及其分类。
这样,式13可更改为:
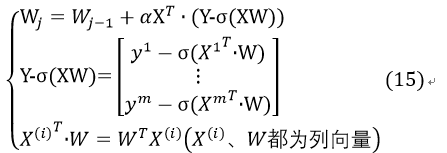
接下来,只需要确定步长α和适宜的迭代次数即可通过X这一训练样本得到符合要求的W,通过W结合logistic sigmoid函数来估计测试数据的分类。
梯度下降法
将对数似然函数乘以一个负系数:

此时可将该式理解为对数损失函数。
此时需要求使得J(W)最小的W值,采用梯度下降法:
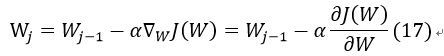
对J(W)求偏导:
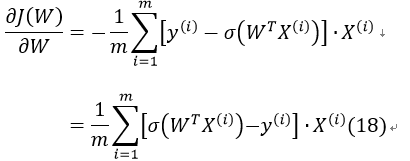
因此式17可改为:
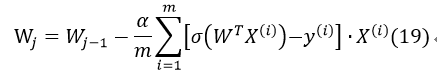
将X,Y改写成矩阵(式14所示),并可将常数1/m省略,则有:
