1. 基本原理
通过一个变换,将输入图像的灰度级转换为`均匀分布`,变换后的灰度级的概率密度函数为
$$P_s(s) = frac{1}{L-1}$$
直方图均衡的变换为
$$s = T(r) = (L-1)int_0^r {P_r(c)} \,{
m d}c $$
- $s$为变换后的灰度级,$r$为变换前的灰度级
- $P_r(r)$为变换前的概率密度函数
2. 测试结果
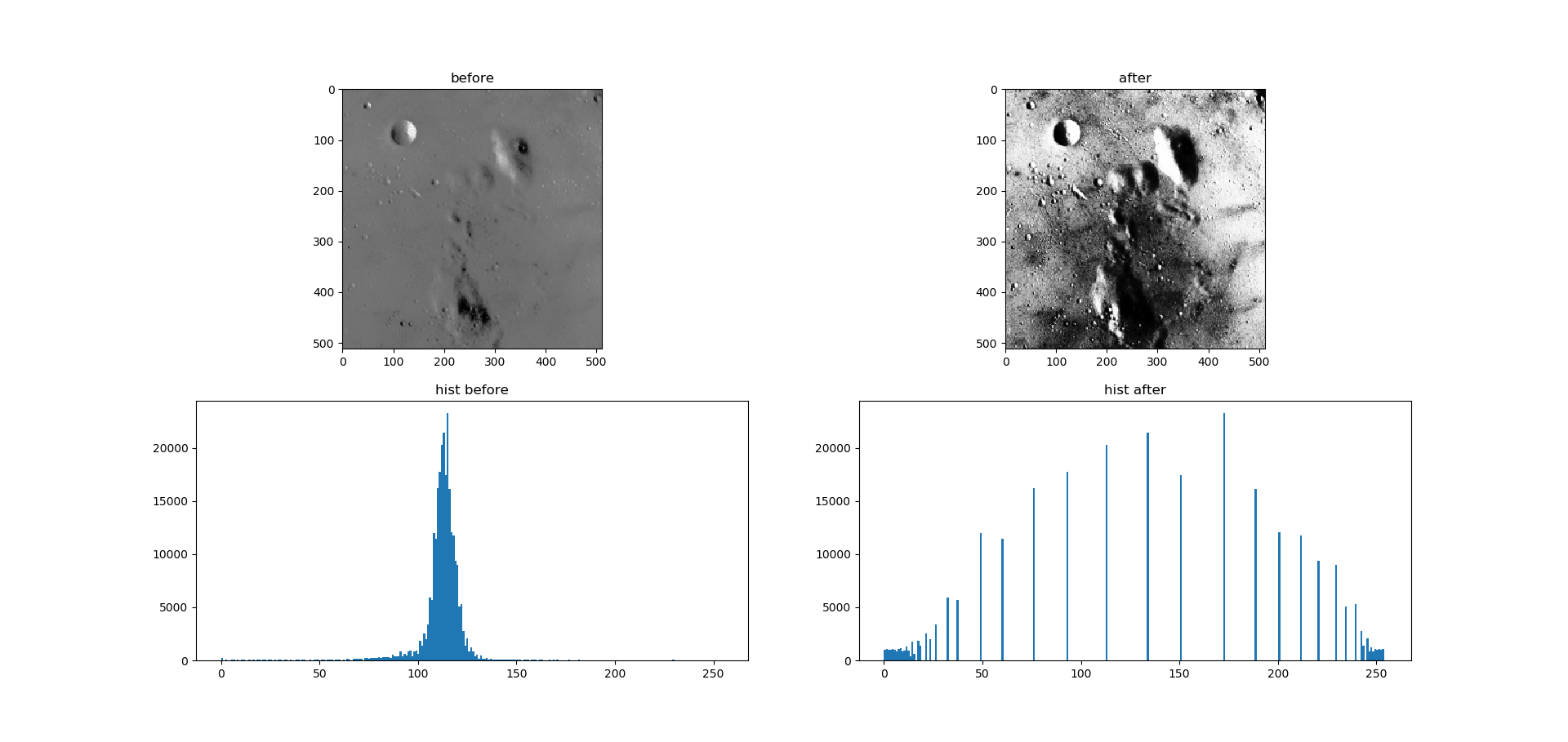
图源自skimage
3.代码
1 import numpy as np 2 3 def hist_equalization(input_image): 4 ''' 5 直方图均衡(适用于灰度图) 6 :param input_image: 原图像 7 :return: 均衡后的图像 8 ''' 9 output_imgae = np.copy(input_image) # 输出图像,初始化为输入 10 11 input_image_cp = np.copy(input_image) # 输入图像的副本 12 13 m, n = input_image_cp.shape # 输入图像的尺寸(行、列) 14 15 pixels_total_num = m * n # 输入图像的像素点总数 16 17 input_image_grayscale_P = [] # 输入图像中各灰度级出现的概率,亦即输入图像直方图 18 19 # 求输入图像中各灰度级出现的概率,亦即输入图像直方图 20 for i in range(256): 21 input_image_grayscale_P.append(np.sum(input_image_cp == i) / pixels_total_num) 22 23 # 求解输出图像 24 t = 0 # 输入图像的灰度级分布函数F 25 for i in range(256): 26 27 t = t + input_image_grayscale_P[i] 28 29 output_imgae[np.where(input_image_cp == i)] = 255 * t 30 31 return output_imgae
4. 数学证明
目标变换
$$S = T(r) = (L-1)int_0^rp_r(w)dw$$
- $T(r)$为严格单调函数,可保证反映射时,消除二义性
- $p_r(w)$为源图像归一化后的直方图
4.1 假定
- 图像灰度级为:$[0, L-1]$
- 源图像中,$k$灰度级的像素个数:$n_k$
- 源图像像素总数:$n$
- 原图像直方图$h(r_k) = n$
4.2 归一化后的直方图
$$p(r_k) = n_k / n$$
$p(r_k)$即为灰度级$r_k$在源图像中出现的概率估计
4.3 证明
概率密度函数的积分为分布函数,即对分布函数的导数为概率密度函数。
因为$p_r(r)$与$T(r)$已知,则由
$$frac{{
m d}r}{{
m d}S} = frac{p_s(s)}{p_r(r)}$$
又因为
$$S = T(r)$$
即
$$frac{{
m d}S}{{
m d}r} = frac{T(r)}{r}$$
联立上三式及目标变换
$$S = T(r) = (L-1)int_0^rp_r(w)dw$$
可得
$$p_s(s) = frac{1}{L-1}$$
故,这意味着变换之后的图像的灰度级为均匀分布,证毕。