矩阵分析与应用笔记 | 国科大李保滨课程总结

目录

• 1 课程介绍
• 2-3 线性方程组
• 4 矩阵代数
• 5 向量空间
• 6 线性变换
  • 基变换
  • 不变子空间
• 7-8 模和内积
  • Norms模--长度
  • Inner Products内积--夹角/几何关系
  • 正交
  • 正交矩阵
  • 互补子空间 Complementary Subspace
  • 值零分解Range-Nullspace Decomposition –方阵
  • 正交分解
  • 奇异值分解
  • 正交投影
• 9 矩阵行列式
• 10 特征值

1 课程介绍

2-3 线性方程组

高斯消去法

交换两行，任意行数乘，一行数乘加到另一行

==> 上三角形

==> 回代

复杂度

乘法 \(\frac {n^3} 3 + n^2 - \frac n 3\)

加法 \(\frac {n^3} 3 + \frac {n^2} 2 - \frac {5n} 6\)

Gauss-Jordan法

多了两个步骤

• pivot变为1
• 消去pivot上面的元素

变换为单位阵

复杂度

乘法 \(\frac {n^3} 2 + \frac {n^2} 2\)

加法 \(\frac {n^3} 2 - \frac {n} 2\)

部分主元法

交换行使主元最大（绝对值）

行阶梯形 定义了矩阵的秩

修改高斯消去法

每行从左到右找非零元，消去后不一定得到上三角形式

秩

• 主元pivot的数量
• 非零行的数量
• 基本列（包含主元）的数量

齐次方程

\([A|0]\)

非齐次方程

右边含有非零数值

平凡解

x=0

[A|b] ==> E[A|b]

解的形式

x = p非齐次方程特解 + (n-r)齐次方程通解

4 矩阵代数

矩阵加法性质

标量乘法性质

共轭转置

对称性

矩阵乘法

不可交换

乘积的行列

\([AB]_{i*} = A_{i*}B\)

\([AB]_{*j} = AB_{*j}\)

分配律 结合律

转置

\((AB)^T = B^TA^T\)

分块乘法

逆矩阵

逆存在性等价描述

• rank(A) = n
• Gauss-Jordan, A –> I
• Ax = 0 ==> x =0

逆的计算

\([A|I] –-> [I|A^{-1}]\)

复杂度 \(n^3\)

\((I+cd^T)^{-1} = I - \frac {cd^T}{1+d^Tc}\)

三种基本行变换

\(E1 = I - uu^T, u = e_1 - e_2\) 交换两行

\(E2 = I - (1-a)e_2e_2^T\) 乘上a倍

\(E3 = I +ae_3e_1^T\) 第一行a倍加到第三行

左乘：基本行变换

相似矩阵

秩相等

推论：与非奇异矩阵的乘法不改变秩

LU分解

A = LU

解方程

LUx = b

Ux = y, Ly = b

5 向量空间

定义 两个集合 \(x\in \mathcal V, \alpha \in \mathcal F\) 两个基本运算：加法和标量乘法

（1）加法封闭

（2）加法结合律

（3）加法交换律

（4）加法零元

（5）加法逆元

（6）数乘封闭

（7）数乘结合律

（8）数乘分配律

（9）数乘分配律

（10）单位元

子空间

是V的子集且满足

（1）加法封闭

（6）数乘封闭

张成集合

\(\mathcal S = {v_1, v_2, …, v_r}\),

子空间 \(span\{\mathcal S \}=\{\alpha_1v_1+\alpha_2v_2+...+\alpha_rv_r\ | \alpha_i \in \mathcal F \}\)

Range Spaces值域空间

列空间

R(A)，相当于\(f(x) = Ax, A \in R^{m \times n}\)，也叫 A 的像空间(image space)

行空间，左值域

\(R(A^T)\)

Nullspace 零空间

• \(N(A)\)

  \(N(f) = \{x_{n\times 1}|Ax=0\}, A \in R^{m\times n}\)

• \(N(A^T)\) 左零空间

  \(N(g) = \{x_{m\times 1}|A^Tx=0\}, A \in R^{m\times n}\)

线性无关

A 的列构成线性无关集合

等价于

• rank(A)=n

• N(A) = {0}

对角占优矩阵是非奇异的

Vandermonde Matrices

\[\mathbf{V}_{m \times n}=\left(\begin{array}{ccccc} 1 & x_{1} & x_{1}^{2} & \cdots & x_{1}^{n-1} \\ 1 & x_{2} & x_{2}^{2} & \cdots & x_{2}^{n-1} \\ \vdots & \vdots & \vdots & \cdots & \vdots \\ 1 & x_{m} & x_{m}^{2} & \cdots & x_{m}^{n-1} \end{array}\right) \]

Wronski matrix

\[\mathbf{W}=\left(\begin{array}{cccc} f_{1}(x) & f_{2}(x) & \cdots & f_{n}(x) \\ f_{1}^{\prime}(x) & f_{2}^{\prime}(x) & \cdots & f_{n}^{\prime}(x) \\ \vdots & \vdots & \ddots & \vdots \\ f_{1}^{(n-1)}(x) & f_{2}^{(n-1)}(x) & \cdots & f_{n}^{(n-1)}(x) \end{array}\right) \]

basis 基

A linearly independent spanning set for a vector space V is called a basis of V.

一组线性无关的张成集合

标准基

\(R^n\) 空间： \(\mathcal S = {e_1, e_2, …, e_n}\)

多项式：{1, x, x^2, … x^n}

{0}：空集

等价命题

• 最小的张成集合
• 最大线性无关子集

维度

等价命题

• V 基的向量个数

• V 最小张成集合的向量个数

• V 最大线性无关子集的向量个数

秩

等价命题

rank(A) \(A \in R^{m \times n}\)

• 等价A的行阶梯矩阵的非零行
• 行阶梯矩阵主元数量
• 基本列数量
• 线性无关列数量
• 线性无关行数量
• dim R(A)
• dim R(A^T)
• n - dim N(A)
• m - dim N(A^T)
• A中最大非奇异矩阵

incidence matrix 入射矩阵

包含 m 个节点 n 条边

每条边对应一列中，一列中包含一组 1， -1 ，对应出点和入点

\[e_{k,j} = \cases{ 1 \text{, 边指向 N_k} \\-1 \text{, 边来自 N_k}\\0} \]

连通图，rank(E) = m - 1

Normal Equations

\(A^TAx = A^Tb\)

\(x = (A^TA)^{-1}A^Tb\)

Rank等价定义

6 线性变换

零变换

恒等变换

线性变换 \(A \in R^{m \times n}\)

从 \(R^n ==> R^m\)

线性算子 \(A \in R^{n \times n}\)

旋转 Q

投影 P

反射 R

有限维空间的线性变换都有矩阵表示

\(\mathcal U\) 空间的向量u 在基 \(\mathcal B = {u_1, u_2, …, u_n}\) 下表示为

\(u = \alpha_1u_1+\alpha_2u_2+...+\alpha_ru_n\)

\(\alpha_i\) 称为 关于B的坐标 \([v]_B = (\alpha_1, \alpha_2, …, \alpha_n)^T\)

线性变换空间

\(\mathcal L(\mathcal U, \mathcal V)\) 表示所有从U变换到V的集合

\(B_{ji}(u) = \xi_jv_i\)， 其中 \((\xi_1, \xi_2, …, \xi_n)^T = [u]_B\)

• 基 \(B_L = \{B_{ji}\}_{j=1...n}^{i=1...m}\)

• dim L(U,V) = (dim U) (dim V)

坐标矩阵表示

每个 u 在 B’ 下的坐标表示作为每一列

坐标变换转化为矩阵乘法

\([T(u)]_{B’} = [T]_{BB’} [u]_{B}\)，其中 \([T]_{BB’}\) 为 u 经过 T 变换后在 v 下的坐标表示。

\([T]_B\) 代表 \([T]_{BB}\)，为方阵

基变换

坐标变换

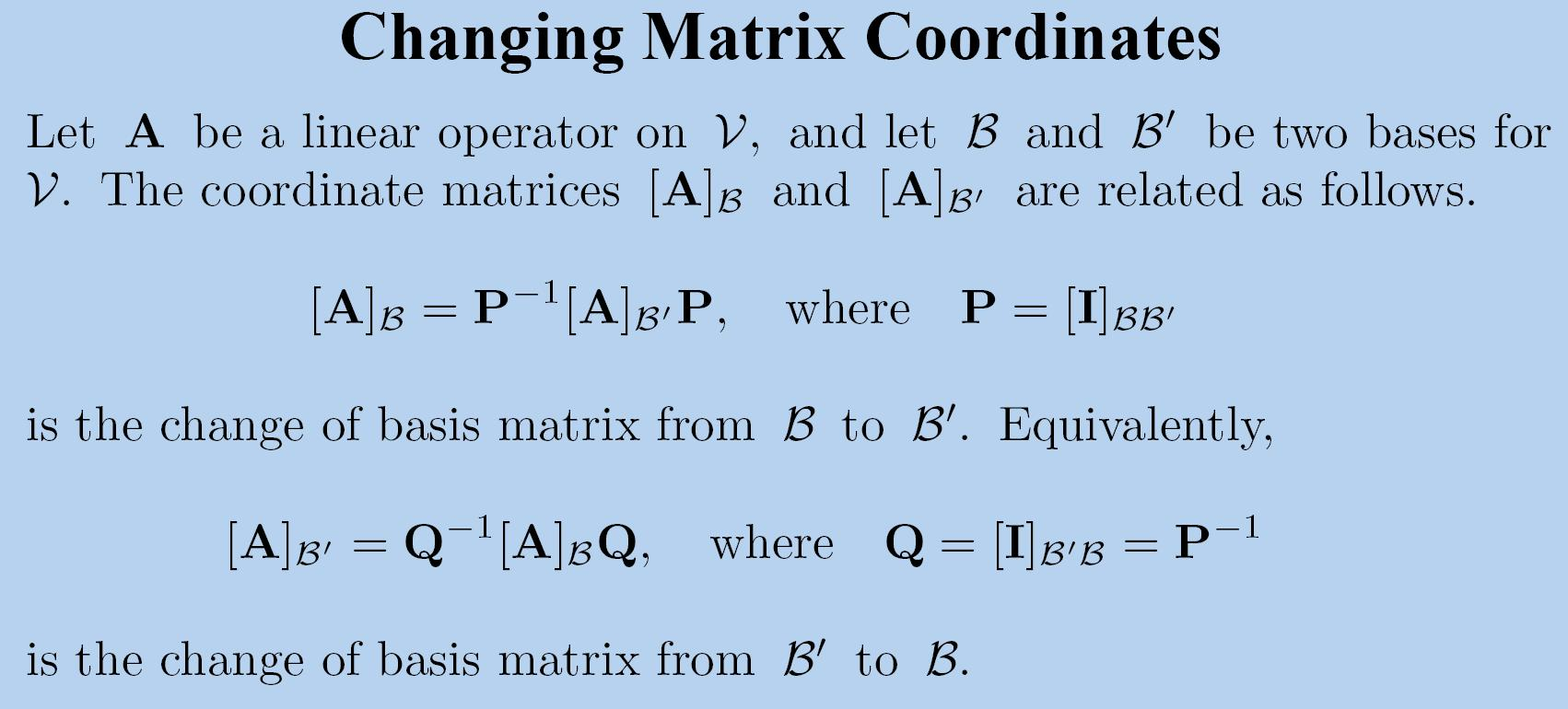
相似性

\(B \simeq C\) ：存在非奇异矩阵Q，使得 \(B = Q^{-1}CQ\) 。

相似变换：\(f: R^{n\times n} \to R^{n \times n}\) ，\(f(C) = Q^{-1}CQ\) 。

不变子空间

定义

• 在变换T下的不变子空间 \(\mathcal{X \subseteq V}\), 且 \(\bold T(\mathcal X) \subseteq \mathcal X\)

• T 这时可以作为一个线性算子，表示为 \(\bold T_{/ \mathcal X}\) 。

上三角和对角块形式

T 是 n x n矩阵，下面的命题是等价的

• \(\mathbf{Q}^{-1} \mathbf{T Q}=\left(\begin{array}{cc} \mathbf{A}_{r \times r} & \mathbf{B}_{r \times q} \\ \mathbf{0} & \mathbf{C}_{q \times q} \end{array}\right)\) 当且仅当 Q 的前 r 列张成 T 下的不变子空间
• \(\mathbf{Q}^{-1} \mathbf{T Q}=\left(\begin{array}{cccc} \mathbf{A}_{r_{1} \times r_{1}} & \mathbf{0} & \cdots & \mathbf{0} \\ \mathbf{0} & \mathbf{B}_{r_{2} \times r_{2}} & \cdots & \mathbf{0} \\ \vdots & \vdots & \ddots & \vdots \\ \mathbf{0} & \mathbf{0} & \cdots & \mathbf{C}_{r_{k} \times r_{k}} \end{array}\right)\) 当且仅当 Q = (Q1|Q2|…|Qk)，每一个 Qi 张成 T 下的不变子空间

7-8 模和内积

Norms模--长度

模：空间几何的概念

范数：线性代数中的概念

向量的模满足

• 正定性 \(\|x\| \ge 0\) 当且仅当 x=0， \(\|x\| = 0\)
• 齐次性
• 三角不等式 \(\|x+y\| \le \|x\| + \|y\|\)

欧几里得模

\(\|x\| = \sqrt{x^Tx}\)

\(\|x\| = \sqrt{x^*x}\) 复数向量

p-模

\(\|x\|_p = (\sum_{i=1}^n\|x_i|^p)^{1/p}\)

矩阵的模满足

• 正定性
• 齐次性
• 三角不等式
• 相容性 \(\|AB\| \le \|A\| \|B\|\)

Frobenius矩阵模

\(\|A\|_F^2=\sum_{i,j}|a_{ij}|^2 = trace(A^*A)\)

矩阵2模

\(\|A\|_2 = \max_{\|x\|_2=1} \|Ax\|_2 = \sqrt {\lambda_{\max}}\) ，其中 \(\lambda\) 为 \(A^*A\) 的最大的特征值。

矩阵1模、无穷模

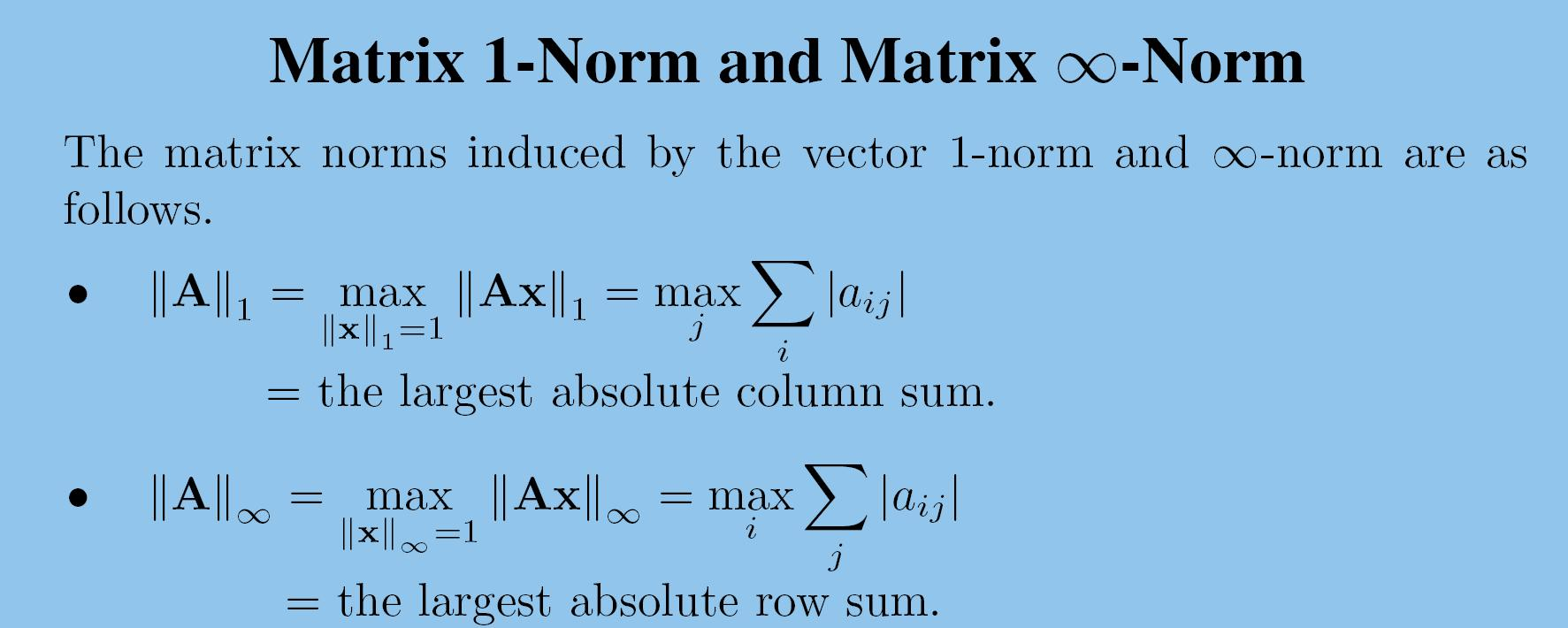
Inner Products内积--夹角/几何关系

内积

标准向量内积 \(<x|y> = x^Ty\)

椭圆内积 \(<x|y> = x^*A^*Ay\)

标准矩阵内积 \(<A|B>=trace(A^TB)\)

内积空间可以定义模：

模等于内积开方

满足平行四边形法则，才有：

内积等于模平方 \(<*|*> = \|*\|^2\)

只有在 p=2情况下 平行四边形法则才满足，因此内积只能产生欧几里得模（二模）

\(\|x+y\|^2 + \|x-y\|^2 = 2(\|x\|^2+\|y\|^2)\)

因为左边p-模等于2* 2^(2/p)，右边p-模恒等于4

正交

正交

\(x \perp y <==> x^Ty=0\)

角度

\(\cos \theta = \frac {<x|y>}{\|x\|\|y\|}\)

标准正交集合/规范正交基

\(<u_i|u_j> =\cases {1 \ \text{when i==j}\\ 0 \ \text{when i/= j}}\)

GramSchmidt施密特正交化

QR分解

把A写成n列，进行施密特正交化分解

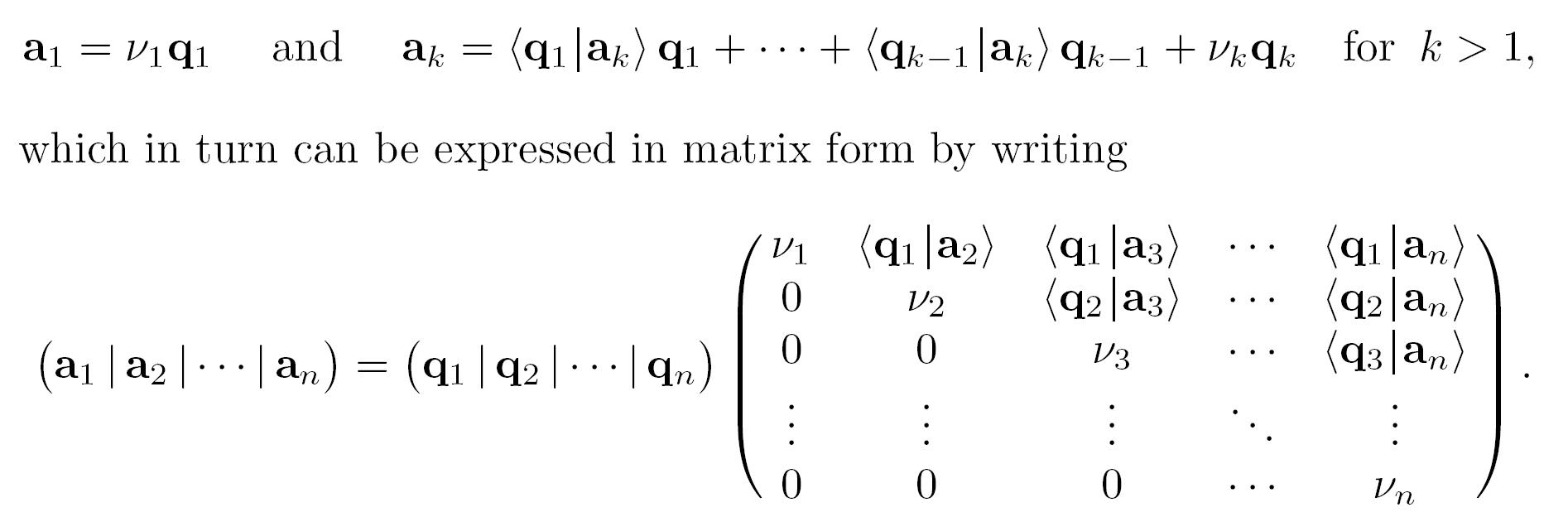
将A分解为 Q R

\(A_{m×n} = Q_{m×n}R_{n×n}\)

如果 \(A \in R^{n\times n}\) 是非奇异矩阵，Q是单位正交基，所以 \(Q^T=Q^{-1}\) 。

\(Ax = b ⇐⇒ QRx = b ⇔ Rx = Q^T b\)

改进的施密特正交化

正交矩阵

酉矩阵和正交矩阵

Unitary and Orthogonal Matrices

酉矩阵（正交矩阵） 列构成标准正交基（复数域、实数域）

\(U^∗U = I ⇐⇒ U^{−1} = U^∗, ⇐⇒ UU^∗ = I\)

与酉矩阵相乘，不改变向量的长度

\(∥Ux∥^2 = x^∗U^∗Ux = x^∗x = ∥x∥2 ∀x ∈ Cn\)

等价命题

• 行 标准正交
• 列 标准正交
• 逆等于转置
• 不改变向量长度

单位矩阵(identity matrix) I是正交矩阵

置换矩阵是正交矩阵

初等正交投影算子

\(Q = I - uu^*\) 投影到u垂直上，其中 \(\|u\|=1\)

正交投影算子

\(P_u = \frac {uu^*}{u^*u}\) 投影到span{u}上

\(P_{u^{\perp}} = I- \frac {uu^*}{u^*u}\) 投影到u垂直上

初等镜面反射算子/Householder变换

\(R = I-2\frac {uu^*}{u^*u}\)

性质 \(R = R^{-1}\) \((由于R^2=I)\)

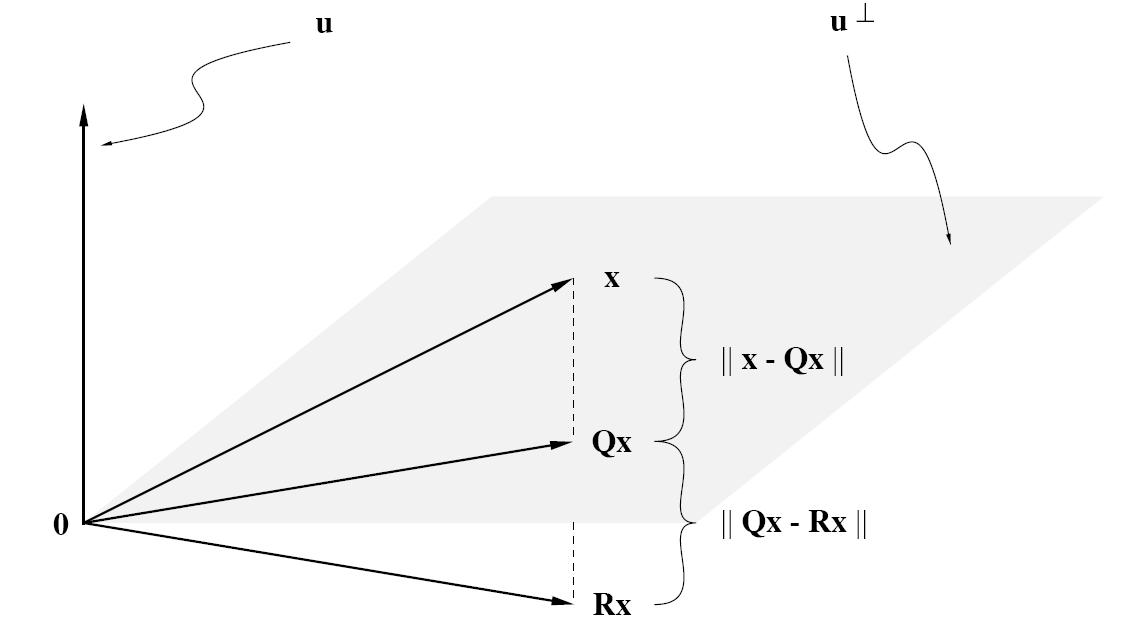
Householder reduction

\(A_{m×n} = [A∗1|A∗2| · · · |A∗n]\)

首先用第一列构造镜面反射算子：

\(R_1 = I − 2\frac {uu^∗} {u^*u}\), \(u = A_{∗1} ± µ\| A_{∗1}\|e_1\)，其中 \(\mu = \cases {1 \ ,x_1 是实数\\ x_1/|x_1| \ ,x_1是复数}\)

使得 \(R_1A_{*1} = ∓ µ\| A_{∗1}\|e_1 = (t_{11},0,\cdots,0)^T\)

平面旋转/Givens旋转

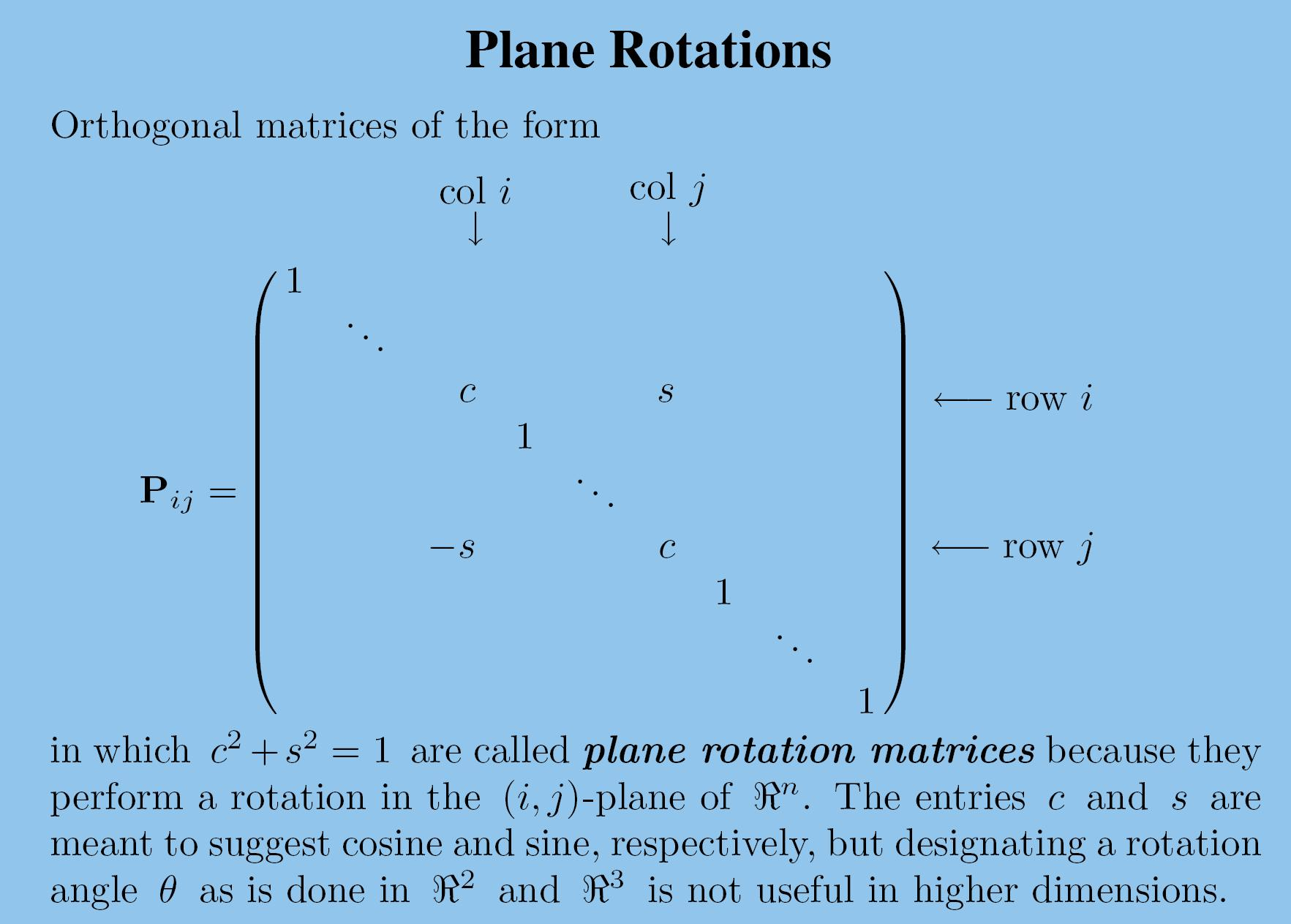
\(P_{ij}x\) 通过旋转，使 \(x_j\) 的坐标值为0

任意向量，旋转到第 i 个坐标轴上，得到 \(Px = \|x\| e_i\)， 其中 \(P = P_{in}\cdots P_{i,i+1}P{i,i-1}\cdots P_{i1}\)

互补子空间 Complementary Subspace

互补子空间

\(\mathcal {V = X+ Y}\) 并且 \(\mathcal {X\cap Y}=0\)

直和

\(\mathcal {V = X\oplus Y}\)

等价命题

• \(\mathcal {V = X\oplus Y}\)
• 任意v，有唯一x, y 使得 v = x + y
• \(B_X \cap B_Y = \emptyset\) 并且 \(B_X \cup B_Y\) 是 V 的基

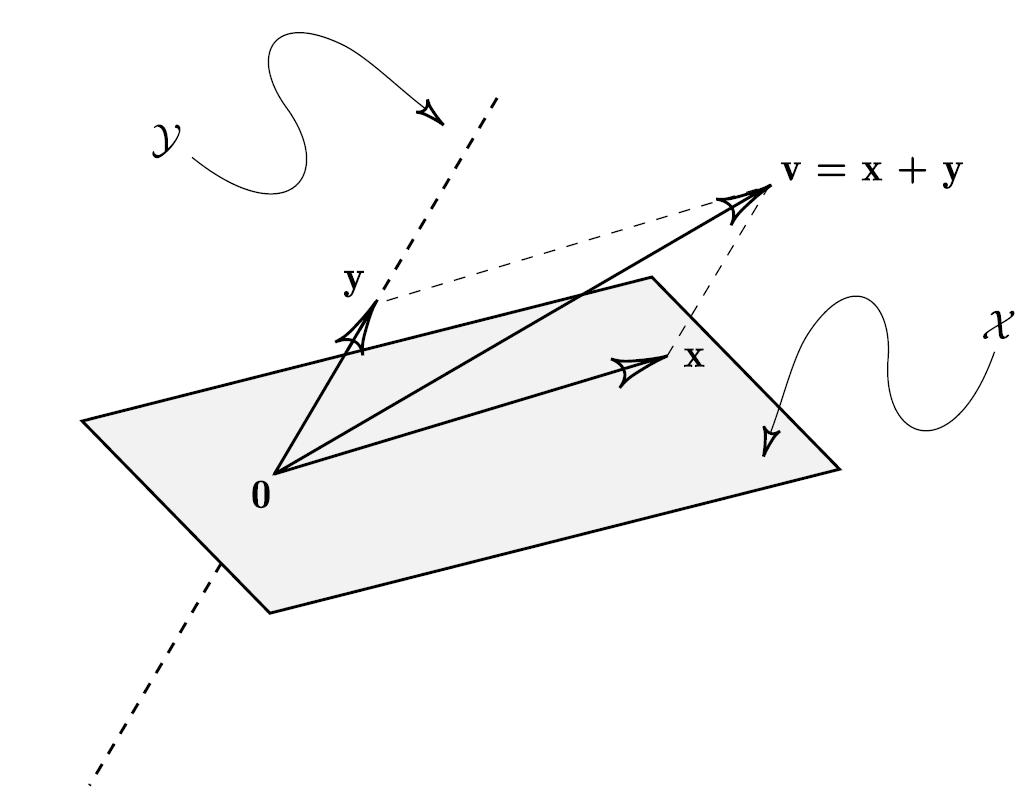
投影

如果 \(\mathcal {V = X\oplus Y}\)， v = x + y

x 被称为 v 沿 Y 到 X 上的投影

y 被称为 v 沿 X 到 Y 上的投影

投影算子

Pv = x

性质

• P^2 = P

• I - P 是互补投影算子（投影到Y）

• R(P)=N(I-P)=X R(I_P)=N(P)=Y

• \(P = [X|0][X|Y]^{-1} = [X|Y]\left[\matrix{I \ 0 \\ 0 \ 0}\right][X|Y]^{-1}\)，其中 X, Y 分别为 \(\mathcal {X, Y}\) 的基。

满足幂等性质的线性算子就是投影算子 P^2 = P

值零分解Range-Nullspace Decomposition –方阵

值零分解

若A是奇异的，则存在k，使得

\(R^n=R(A^k)⊕N(A^k)\)，其中 最小的 k 为 A 的 index

若A是非奇异的， 定义index(A)=0

求index

计算 A^k, A^{k+1} 秩不变

幂零矩阵 N^k = 0

核零分解 Core-Nillpotent分解

通过相似变换

\(Q^{-1}AQ = \left(\matrix{C_{r\times r} 0\\ 0 N}\right)\)，其中 rank(A^k) = r , N^k = 0

Drazin Inverse

方阵

\[\mathbf{A}=\mathbf{Q}\left(\begin{array}{ll} \mathbf{C} & 0 \\ 0 & \mathbf{N} \end{array}\right) \mathbf{Q}^{-1}, \text { then } \mathbf{A}^{D}=\mathbf{Q}\left(\begin{array}{ll} \mathbf{C}^{-1} & 0 \\ 0 & 0 \end{array}\right) \mathbf{Q}^{-1} \]

\(A^DAA^D = A^D,AA^D = A^DA, A^{k+1}A^D = A^k\)， 其中 k = index(A)

正交分解

正交补

与 W 正交的所有向量的集合 \(W^\perp\)

正交补子空间

M 是 V 的子空间，则

\(\mathcal {V = M\oplus M^{\perp}}\)

若 \(\mathcal {V = M\oplus N}\) 并且 \(\mathcal {N \perp M}\)

那么 \(\mathcal {N = M^{\perp}}\)

垂直运算

• \(\dim M^{\perp} = n - \dim M\)

• \(M^{\perp ^\perp} = M\)

正交分解理论

对于任意矩阵 A，都有：

• \(R(A) ^{\perp}= N(A^T)\)
• \(N(A)^{\perp}= R(A^T)\)
• \(R^m = R(A) \oplus N(A^T)\)
• \(R^n = N(A) \oplus R(A^T)\)

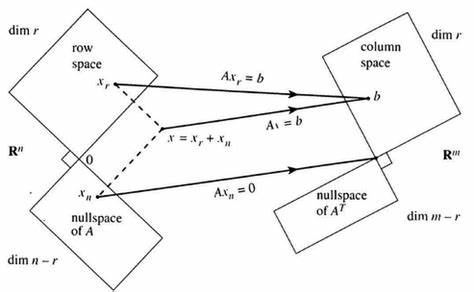
矩阵的四个基本子空间

• R(A) 是行空间 \(N(A^T)\) 的正交补
• N(A) 是行空间 \(R(A^T)\) 的正交补

URV分解 – 非方阵

数值计算稳定

每个 \(A \in R^{m \times n}\) 都有 正交矩阵U， V 和非奇异矩阵 C

\[\mathbf{A}=\mathbf{U R V}^{T}=\mathbf{U}\left(\begin{array}{cc} \mathbf{C}_{r \times r} & \mathbf{0} \\ \mathbf{0} & \mathbf{0} \end{array}\right)_{m \times n}V^{T} \]

• U 的前 r 列是 R(A) 的标准正交基
• U 的后 m-r 列是 R(A)垂直/N(A^T) 的标准正交基
• V 的前 r 列是 N(A)垂直/R(A^T) 的标准正交基
• V 的后 n-r 列是 N(A) 的标准正交基

RPN矩阵 Range Perpendicular to Nullspace

也叫 值域对称矩阵，EP矩阵

非奇异矩阵是平凡 RPN矩阵，零空间是 0

正规矩阵 AA* = A*A

Hermitian A=A*

对称矩阵 A = A^T

等价命题 R(A) = R(A^T)

• \(R(A) {\perp} N(A)\)
• \(R(A)= R(A^T)\)
• \(N(A)= N(A^T)\)
• \(\mathbf{A}=\mathbf{U}\left(\begin{array}{cc} \mathbf{C}_{r \times r} & \mathbf{0} \\ \mathbf{0} & \mathbf{0} \end{array}\right)U^{T}\)

奇异值分解

每个 \(A \in R^{m \times n}\) 都有 正交矩阵U， V 和对角矩阵 \(D=diag(\sigma_1, \sigma_2, …, \sigma_r)\)

\(\mathbf{A}=\mathbf{U}\left(\begin{array}{cc} \mathbf{D} & \mathbf{0} \\ \mathbf{0} & \mathbf{0} \end{array}\right)_{m \times n}V^{T}\)

应用

• 对单位球变换的拉伸度量
• 线性系统敏感性分析
• 最近的 rank(k)矩阵距离 $ \min |A-B|_2$
• 整理嘈杂的数据，提取相关信息，相当于傅里叶展开

伪逆（非方阵）

满足四条 Penrose方程

AA†A = A, A†AA† = A†, (AA†)T = AA†, (A†A)T = A†A

正交投影

每对互补子空间定义了一个投影算子

当子空间互相垂直，则为正交投影

定义

v = m + n， \(m \in M\) 并且 \(n \in M^{\perp}\)

• m 被称为 v 到 M 上的正交投影
• \(P_{M}\) 沿着 \(M^{\perp}\) 到 M 上的投影算子
• \(P_{M}v = m\)

构造投影算子

M 是 \(\mathcal M\) 的基，则

• \(P_{M}=M(M^TM)^{-1}M^T\) , \(P_{M^{\perp}}=N(N^TN)^{-1}N^T\)

M 包含标准正交基

• \(P_M = MM^T\)
• \(P_{M} = (M|N)\left( \matrix{I_r 0 \\ 0 0}\right)(M|N)^T\)
• \(P_{M^{\perp}}=I-P_M\)

正交投影算子

投影算子P 是正交投影算子

等价命题

• \(R(P) \perp N(P)\)
• \(P^T = P\)
• \(\|P\|_2 = 1\)

最近点理论

M 是 内积空间 V 的子空间， b 是 V 的向量，M 上离 b 最近的向量是

p = PMb， b 到 M 上的正交投影

b 和 M 的正交距离：

\[\min _{\mathbf{m} \in \mathcal{M}}\|\mathbf{b}-\mathbf{m}\|_{2}=\left\|\mathbf{b}-\mathbf{P}_{\mathcal{M}} \mathbf{b}\right\|_{2}=\operatorname{dist}(\mathbf{b}, \mathcal{M}) \]

最小平方解

等价命题

• \(\left\|\mathbf{A \hat x} - \mathbf{b}\right\|_{2}= \min _{x \in R^n}\left\|\mathbf{Ax} - \mathbf{b}\right\|_{2}\)

• \(A\hat x = P_{R(A)}b\)

• \(A^TA\hat x = A^Tb\)

• \(\hat x \in A^{+}b + N(A)\)

9 矩阵行列式

定义

\(\det (\bold A) = \sum _p \sigma(p)a_{1p_1}a_{2p_2}\cdots a_{np_n}\)，其中 \(\sigma(p) = \cases {+1\ p是偶排列\\-1\ p是奇排列 }\)

行列式表示也可以用 \(|\bold A|\)

行操作对行列式的影响

两行交换：det(B) = - det(A)

某行数乘：det(B) = a det(A)

i 行 a 倍加到 j 行：det(B) = det(A)

可逆性与行列式

• 非奇异 <==> det(A) /= 0
• 奇异 <==> det(A) = 0

乘积法则

det(AB) = det(A)3det(B) 所有n x n矩阵

\(\det(\matrix{A \ B \\ 0 \ D}) = \det(A) \det(D)\) A，D为方阵

行列式计算

PA = LU

\(\det(A) = \sigma u_{11}u_{22}\cdots u_{nn}\)，\(\sigma\) 根据行交换次数奇偶性确定

行列式微分

\(A_{n\times n} = [a_{ij}(t)]\) 的元素是 t 的可微函数

\(\frac {d(\det(A)) } {dt} = \det(D_1) + \det(D_2) + \cdots + det(D_n)\)，其中 \(D_i\) 表示 A 的第 i 行被该行的微分替代。

秩1矩阵更新

\(\det(I+cd^T) = 1 + d^Tc\)

\(\det(A+cd^T) = \det(A)(1 + d^TA^{-1}c)\)

克莱姆法则

\(x_i = \frac {\det(A_i)} {\det(A)}\)，其中 \(A_i\) 表示 A 的第 i 列替换为 b

代数余子式

\(\AA_{ij}=(-1)^{i+j}M_{ij}\)

求逆

adjugate 伴随矩阵 adj(A) = \(\AA^T\) 代数余子式构成的矩阵的转置

adjoint 伴随矩阵 \(A^*\)

\(A^{-1} = \frac {\AA^T} {\det(A)}\)

10 特征值

定义

\(Ax = \lambda x\)，其中 \(\lambda\) 和 x 被称为特征值和特征向量

\(\sigma(A)\) 特征值集合， A的频谱spectrum

\(\lambda \in \sigma(A) <==> A-\lambda I 是奇异矩阵 <==> \det(A-\lambda I)=0\)

特征方程

A的行列式 为 特征值之积

A的迹 为 特征值之和

谱半径

A 的最大特征值的绝对值

相似变换对角化

相似性

\(P^{-1}AP = B\) 则A 与 B 相似，左边为A的相似变换

可对角化

A 相似于对角阵 <=> A 有 n 个特征向量 <=> \(P^{-1}AP=diag(\lambda…)\),P每一列为特征向量​

代数重数

特征方程的指数

几何重数

\(geo\ mult_A(\lambda)=dim N(A-\lambda I) \leq alg \ mult_A(\lambda)\)

对于每个特征值，代数重数等于几何重数，等价于 A 可对角化

频谱分解

)

正规矩阵

\(A^*A = AA^*\) <==> A 可酉对角化，被称为正规矩阵

性质

• A 是 RPN矩阵

• R(A − λiI)⊥N(A − λiI).

对称矩阵和Hermitian矩阵

A 是 实对称矩阵 <==> A 正交相似于 实对角矩阵 \(P^TAP = D\)

正定矩阵

等价定义

• \(x^TAx>0\)

• 对称矩阵A的特征值是正数

• \(A=B^TB\) 能分解为非奇异矩阵

• LU分解后，主元为正

• 顺序主子式为正

• 主子式为正

二次型

\(f(x) = x^TAx\)