1493: 平面划分

http://www.acmore.net/problem.php?id=1493

Time Limit: 1 Sec Memory Limit: 128 MB
Submit: 139 Solved: 32

Description

一条直线能够将平面分成2部分，两条直线能够将平面分成4部分，而对于一条“V”型线而言，平面被分成2部分，两条“V”型线最多能够将平面分成7部分。对于椭圆封闭曲线对平面的划分又将不一样，任意两个椭圆至多有两个交点。现在给定一个N，你能够计算出三种不同情况下，空间最多被划分出多少个部分吗？

Input

若干组测试数据，每组测试数据占一行，每行一个正整数N（1<=N<=10^6）。

Output

每组数据输出一行，每行3个整数，之间用空格隔开。

分别输出N条直线，N条“V”型线，和N个椭圆最多能够将平面划分成多少部分，结果保证在10^18以内？

Sample Input

Sample Output

2 2 2

4 7 4

HINT

Source

Lyush

推理题：

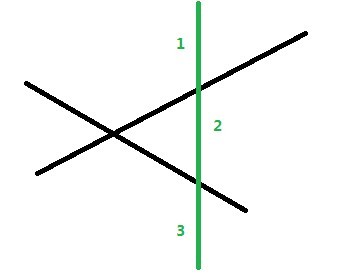
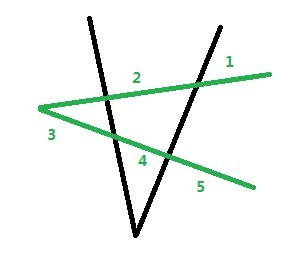
新加入的一条直线与前面的直线都相交能够得到最多的空间划分。考虑到绿色的线是第三根插入的线，那么标号为1,2,3的线就是新区域的边界。对于如图加入第二个V型线，新增5个区域。如果增加第三个椭圆，新增4个区域。最后推出对于直线f[i] = f[i-1] + i；对于V型线f[i] = f[i-1] + 4*i-3；对于椭圆f[i] = f[i] + 2*i-2。

 1 #include<iostream>
 2 #include<cstdio>
 3 #include<cstring>
 4 
 5 using namespace std;
 6 
 7 const int maxn=1000010;
 8 
 9 long long f1[maxn],f2[maxn],f3[maxn];
10 
11 void Init(){
12     f1[1]=f2[1]=f3[1]=2;
13     for(int i=2;i<=1000000;i++){
14         f1[i]=f1[i-1]+i;
15         f2[i]=f2[i-1]+4*i-3;
16         f3[i]=f3[i-1]+2*i-2;
17     }
18 }
19 
20 int main(){
21 
22     //freopen("input.txt","r",stdin);
23 
24     int n;
25     Init();
26     while(scanf("%d",&n)!=EOF){
27         printf("%lld %lld %lld\n",f1[n],f2[n],f3[n]);
28     }
29     return 0;
30 }