POJ 3020 Antenna Placement

Antenna Placement

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 5302		Accepted: 2645

Description

The Global Aerial Research Centre has been allotted the task of building the fifth generation of mobile phone nets in Sweden. The most striking reason why they got the job, is their discovery of a new, highly noise resistant, antenna. It is called 4DAir, and comes in four types. Each type can only transmit and receive signals in a direction aligned with a (slightly skewed) latitudinal and longitudinal grid, because of the interacting electromagnetic field of the earth. The four types correspond to antennas operating in the directions north, west, south, and east, respectively. Below is an example picture of places of interest, depicted by twelve small rings, and nine 4DAir antennas depicted by ellipses covering them. 
 
Obviously, it is desirable to use as few antennas as possible, but still provide coverage for each place of interest. We model the problem as follows: Let A be a rectangular matrix describing the surface of Sweden, where an entry of A either is a point of interest, which must be covered by at least one antenna, or empty space. Antennas can only be positioned at an entry in A. When an antenna is placed at row r and column c, this entry is considered covered, but also one of the neighbouring entries (c+1,r),(c,r+1),(c-1,r), or (c,r-1), is covered depending on the type chosen for this particular antenna. What is the least number of antennas for which there exists a placement in A such that all points of interest are covered? 

Input

On the first row of input is a single positive integer n, specifying the number of scenarios that follow. Each scenario begins with a row containing two positive integers h and w, with 1 <= h <= 40 and 0 < w <= 10. Thereafter is a matrix presented, describing the points of interest in Sweden in the form of h lines, each containing w characters from the set ['*','o']. A '*'-character symbolises a point of interest, whereas a 'o'-character represents open space. 

Output

For each scenario, output the minimum number of antennas necessary to cover all '*'-entries in the scenario's matrix, on a row of its own.

Sample Input

2
7 9
ooo**oooo
**oo*ooo*
o*oo**o**
ooooooooo
*******oo
o*o*oo*oo
*******oo
10 1
*
*
*
o
*
*
*
*
*
*

Sample Output

17
5

Source

Svenskt Mästerskap i Programmering/Norgesmesterskapet 2001

 

 

题目大意：

一个矩形中，有N个城市’*’，现在这n个城市都要覆盖无线，若放置一个基站，那么它至多可以覆盖相邻的两个城市。
问至少放置多少个基站才能使得所有的城市都覆盖无线？

解题思路：

思前想后，依稀可以认为是一道求二分图的最小路径覆盖问题

（注意不是最小点覆盖）

那么接下来需要确认的是，

究竟是求 有向二分图的最小路覆盖，还是求 无向二分图的最小路覆盖

因为有向和无向是截然不同的计算方法。

要确认是构造有向图，还是构造无向图，那么就需要先根据题意，看看构造二分图时所使用的方式，更适合构造哪一种二分图。

然后就进入了本题难点：如何构造二分图

首先要明确的是，输入的一堆“圈圈星星”可以看做是一张大地图，地图上有所有城市的坐标，但是这里有一个误区：不能简单地把城市的两个x、y坐标作为准备构造的二分图的两个顶点集。

城市才是要构造的二分图的顶点！

构造方法如下：

例如输入：

*oo

***

O*o

时，可以抽象为一个数字地图：

100

234

050

数字就是根据输入的城市次序作为该城市的编号，0代表该位置没有城市。

然后根据题目的“范围”规则，从第一个城市开始，以自身作为中心城市，向四个方向的城市进行连线（覆盖）

因此就能够得到边集：

e12  e21     e32     e43    e53

     e23     e34

             e35

可以看到，这些边都是有向边，但是每一条边都有与其对应的一条相反边。

即任意两个城市（顶点）之间的边是成对出现的

那么我们就可以确定下来，应该 构造无向二分图（其实无向=双向）

因为若要构造有向的二分图时，需要判断已出现的边，是很麻烦的工作

为了把有向图G构造为无向二分图，这里需要引入一个新名词“拆点”

其实就是把原有向图G的每一个顶点都”拆分（我认为复制更准确）”为2个点，分别属于所要构造的二分图的两个顶点集

例如在刚才的例子中抽出一条有向边e12举例说明：

复制顶点1和顶点2，使得1，2∈V1；  1’，2’∈V2 ，不难发现|V1|=|V2|

根据边e12和e21，得到无向二分图：

 

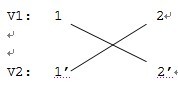
那么同理就可以得到刚才的例子的 无向二分图为：

 

再继而通过无向二分图，以V1的元素作为row，V2的元素作为col，构造 可达矩阵 存储到计算机

   1’  2’  3’  4’  5’

1  F  T   F   F   F

2  T  F   T   F   F

3  F  T   F   T   T

4  F  F   T   F   F

5  F  F   T   F   F

接下来就是要求这个 无向二分图的最小路径覆盖 了

利用公式：

无向二分图的最小路径覆盖 = 顶点数 – 最大二分匹配数/2

顶点数：就是用于构造无向二分图的城市数，即进行“拆点”操作前的顶点数量

最大二分匹配书之所以要除以2，是因为进行了“拆点”擦奥做做使得匹配总数多了一倍，因此除以2得到原图的真正的匹配数

最后剩下的问题就是求最大二分匹配数了，用匈牙利算法，这就不多说了，参考POJ3041的做法，基本一摸一样。
从这道题得出了一个结论：

当二分图的两个顶点子集基数相等时，该二分图所有顶点的匹配数 等于 任意一个顶点子集匹配数的2倍

（注：以上报告摘自 http://blog.csdn.net/lyy289065406/article/details/6647040 ）

 

 

#include<iostream>
#include<cstdio>
#include<cstring>

using namespace std;

int n,m,cnt,map[2520][2520],linker[2520],vis[2520];
int g[60][60],tg[60][60];
char str[60][60];

int DFS(int u){
    int v;
    for(v=1;v<=cnt;v++)
        if(map[u][v] && !vis[v]){
            vis[v]=1;
            if(linker[v]==-1 || DFS(linker[v])){
                linker[v]=u;
                return 1;
            }
        }
    return 0;
}

int Hungary(){
    int u,ans=0;
    memset(linker,-1,sizeof(linker));
    for(u=1;u<=cnt;u++){
        memset(vis,0,sizeof(vis));
        if(DFS(u))
            ans++;
    }
    return ans;
}

int main(){

    //freopen("input.txt","r",stdin);

    int t;
    scanf("%d",&t);
    while(t--){
        scanf("%d%d",&n,&m);
        cnt=0;
        memset(g,0,sizeof(g));
        for(int i=0;i<n;i++){
            scanf("%s",str[i]);
            for(int j=0;j<m;j++)
                if(str[i][j]=='*')
                    g[i][j]=++cnt;
        }
        //printf("cnt=%d\n",cnt);
        memset(map,0,sizeof(map));
        for(int i=0;i<n;i++)
            for(int j=0;j<m;j++)
                if(str[i][j]=='*'){
                    if(i>0 && str[i-1][j]=='*')
                        map[g[i][j]][g[i-1][j]]=1;
                    if(i<n-1 && str[i+1][j]=='*')
                        map[g[i][j]][g[i+1][j]]=1;
                    if(j>0 && str[i][j-1]=='*')
                        map[g[i][j]][g[i][j-1]]=1;
                    if(j<m-1 && str[i][j+1]=='*')
                        map[g[i][j]][g[i][j+1]]=1;
                }
        int ans=Hungary();
        //printf("ans=%d\n",ans);
        printf("%d\n",cnt-ans/2);
    }
    return 0;
}