数据结构1---红黑树

^红黑树

红黑树本质上也是二叉查找树，但是红黑树是一种含有红黑结点并且能够自动平衡的二叉查找树

1、红黑树的原则：

1、所有结点要么是红色要么是黑色
2、根结点必须是黑色
3、叶子结点必须是黑色（NIL结点）
4、红结点的两个子结点必须是黑色
5、任意一结点到每个叶子结点的路径都包含数量相同的黑结点

红黑树和AVL树的区别是AVL树是完全平衡二叉树，保证了每个结点的左右子树的深度差不会大于1，而红黑树根据性质5可以推论出红黑树是不关心左右子树的深度的，
只需要保证每个结点到其所有叶子结点到路径中包含到黑色结点数量相等即可。所以每个结点要么没有黑色子结点，要么肯定是有两个黑色子结点
红黑树不是完美平衡二叉树，不保证左右子树的高度差，只保证左右子树的黑色结点的层数相等，所以是遵循黑色完全平衡规律。

和平衡二叉树一样，红黑树为了达到自身的平衡规律，在增删结点时也需要对整个树进行平衡调整，主要分成三步：
左旋：以某个结点作为支点(旋转结点)，其右子结点变为旋转结点的父结点，右子结点的左子结点变为旋转结点的右子结点，左子结点保持不变

右旋：以某个结点作为支点(旋转结点)，其左子结点变为旋转结点的父结点，左子结点的右子结点变为旋转结点的左子结点，右子结点保持不变

变色：将黑色变成红色；将红色变成黑色

其中左旋和右旋和平衡二叉树的逻辑基本上一致，只是额外增加了变色的调整规则。
另外红黑树每次插入新结点，都是红色的，因为如果是黑色的，就必然会导致红黑树结构变得不平衡了，因为这个黑结点的父结点只有这一个子结点，就破坏了红黑树的第五个性质。

2、红黑树变色旋转规则

左旋：以某个结点作为支点(旋转结点),其右子结点变成支点的父结点，右子结点的左子结点变成支点的右子结点，左子结点不变；且右子结点替代支点成为原父结点的子结点

如下图示(图中红黑色非红黑树的颜色，只是黑色表示需要左旋操作的相关结点)

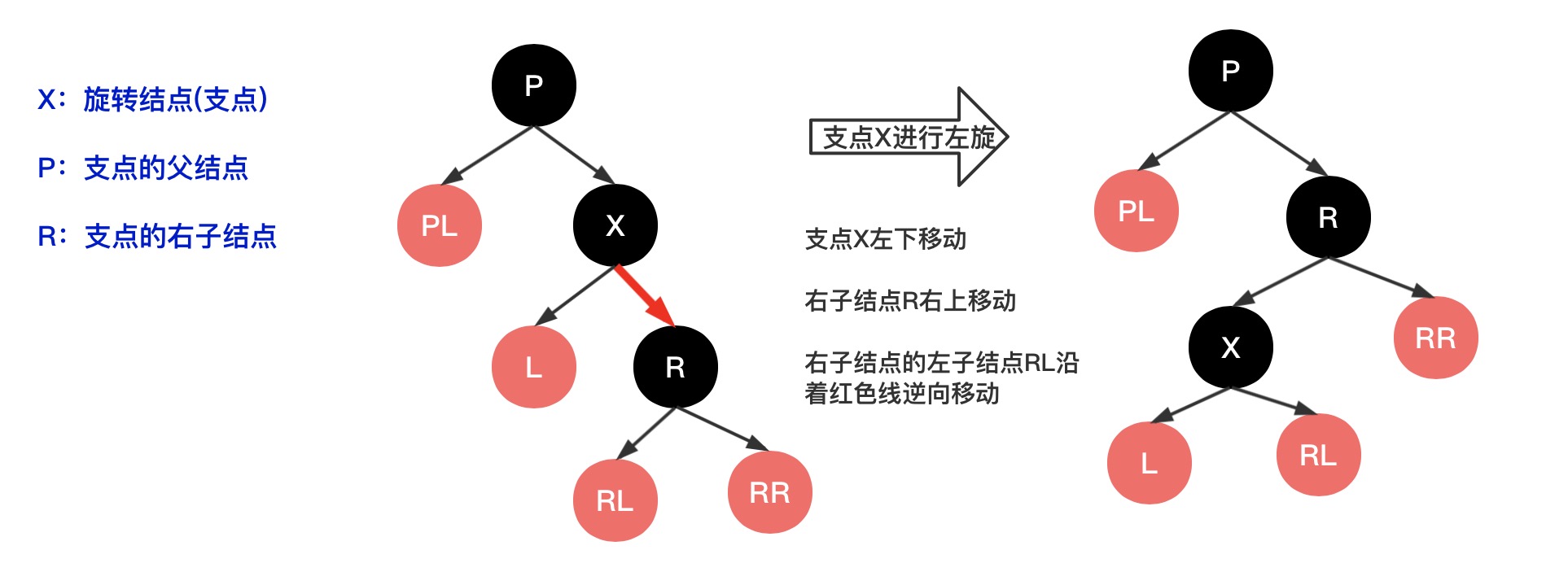
以支点X和右子结点R为点，两个点之间的连线比如叫做 结线 (临时简称),可以看出左旋之前的 结线 是""，而左旋之后变成了 "/",然后将右子结点变成父结点的子结点，右子结点的左子结点变成支点的右子结点即可

右旋：以某个结点作为支点(旋转结点)，其左子结点变成支点的父结点，左子结点的右子结点变成支点的左子结点，右子结点不变；且左子结点替代支点成为原父结点的子结点

如下图示(图中红黑色非红黑树的颜色，只是黑色表示需要左旋操作的相关结点)

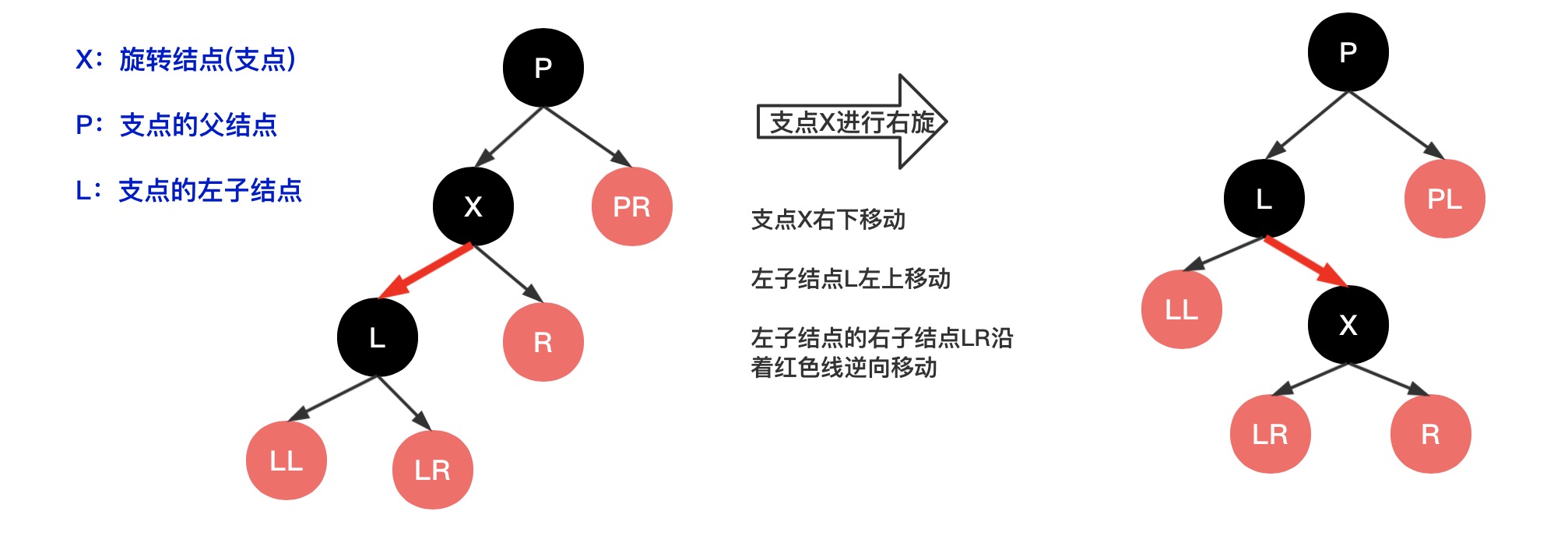
可以看出右旋和左旋的逻辑完全相反

总结：

左旋：

1、支点和右子结点的连线方向从 变成 /

2、右子结点成支点父结点的子结点，且成为支点点父结点

3、支点成为右子结点的左子结点

4、右子结点的左子结点变成支点的右子结点

右旋：

1、支点和左子结点的连线方向从 / 变成

2、左子结点成支点父结点的子结点，且成为支点点父结点

3、支点成为左子结点的右子结点

4、左子结点的右子结点变成支点的左子结点

变色方案：

1、新点为根结点则变色为黑色

2、父结点和右叔结点为红色，则将父结点和右叔结点变成黑色，将爷结点变成红色

3、父结点为红色，右叔结点不存在或为黑色，则选择之后(如有需要)，将父结点变成黑色，爷结点变成红色

3、红黑树插入结点的整体流程流程（假设将新插入的结点简称为 新点）

（插入的逻辑和二叉查找树一样，先找到指定位置，直接插入，只是插入之后需要做一下的平衡操作）

1、将新点颜色变色为红色（新插入结点颜色为红色）

2、将新点作为起点进行递归以下逻辑判断，直到新点达到以下任何一个流程结束的条件（流程结束的条件是没有父结点或者父结点颜色为黑色）

3、如果新点没有父结点，则表示新点为根结点，将新点变色为黑色，流程结束（如下图例子1）

4、如果新点有父结点，且父结点颜色为黑色，由于不会破坏红黑树结构，无需平衡操作，流程结束（如下图例子2）

5、如果新点有父结点，且父结点颜色为红色，根据红黑树原则的值，父结点肯定还有父结点，所以新点必然有爷结点，则有以下多种情况：

5.1、父结点是爷结点的左子结点（如下图例子4）

 5.1.1、右叔结点不为空，且右叔结点是红结点，则将父结点和右叔结点变成黑结点，将爷结点变成红结点，然后将爷结点作为新点，继续从第2步开始执行

 5.1.2、右叔结点为空,或者右叔结点是黑结点（如下图例子7）

   5.1.2.1、如果新点是父结点的右子结点（如下图例子7），则需要先对父结点进行一次左旋操作，使得新点成为父结点的父结点，父结点成为新点的左子结点，然后将父结点作为新点继续从第2步开始执行

   5.1.2.2、如果父结点不为空，则将父结点变色黑色

   5.1.2.3、如果爷结点不为空，则将爷结点变成红色，并且将爷结点作为新点继续从第2步开始执行（如下图例子7）

5.2、父结点是爷结点的右子结点（流程和5.1完全一致，逻辑完全左右相反即可，有兴趣可自行总结）

纸上得来终觉浅，下面在实际案例中来具体分析，如下从无到有依次插入8个结点的完整流程
1、插入第一个结点，值为100，如下图示

插入新结点，结点颜色为红色，由于是根结点，所以需要变色成黑色结点

2、插入第二个结点，值为120，如下图示

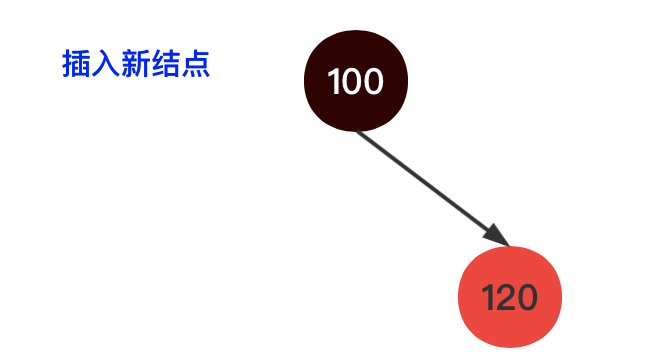
插入新红结点，由于比100大，所以是根结点的右子结点，不会破坏红黑树结构，插入结束

3、插入第三个结点，值为150，如下图示

插入新红结点150，由于比100和120都大，所以是120结点的左子结点；由于120结点是红色，破坏了红黑树的第4个规则，所以150结点需要变色成黑色；此时根结点左边黑结点层数为0，右边为1，破坏了红黑树第5个原则，所以需要进行左旋操作；

此时120结点为新的根结点，此时由于120为红色结点，又破坏了红黑树的第2个原则，继续进行变色操作，最终如上图示。

4、插入新结点，值为80，如下图示

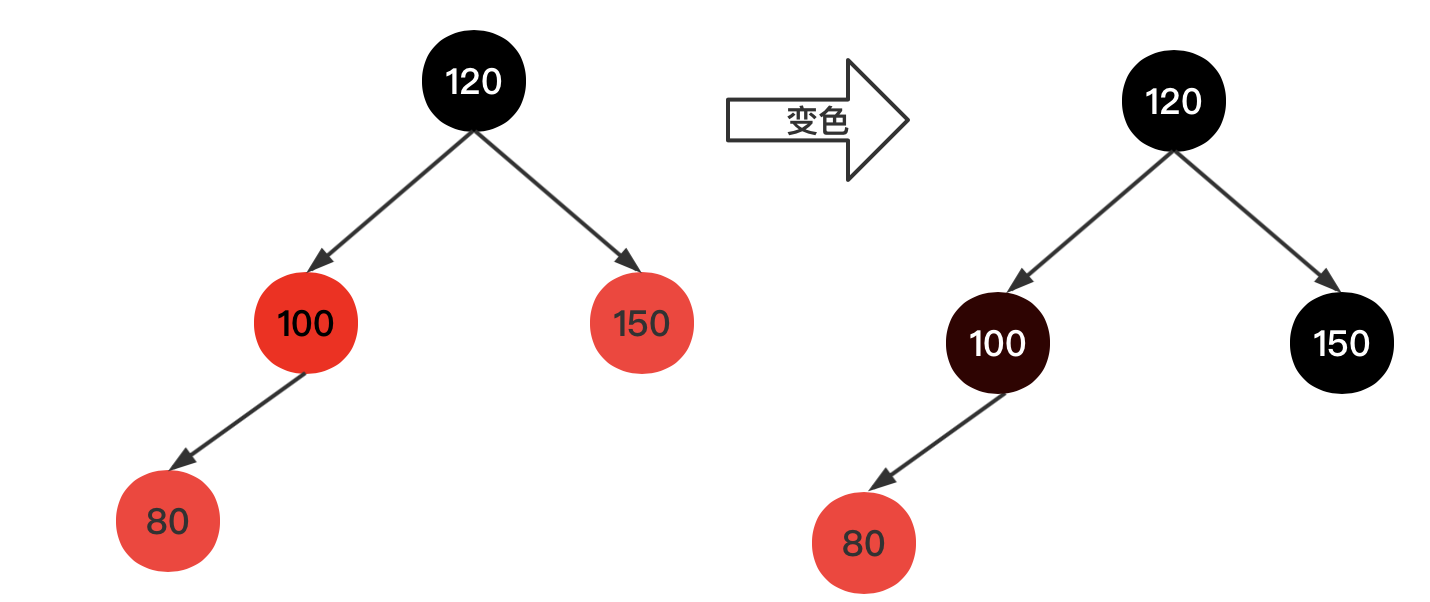
插入新红结点80，由于父结点100为红色，所以需要进行变色操作，将父结点和叔结点都变色成黑色，爷结点变成红色，由爷结点是根结点，所以再变成黑色

5、插入新结点，值为60，如下图示

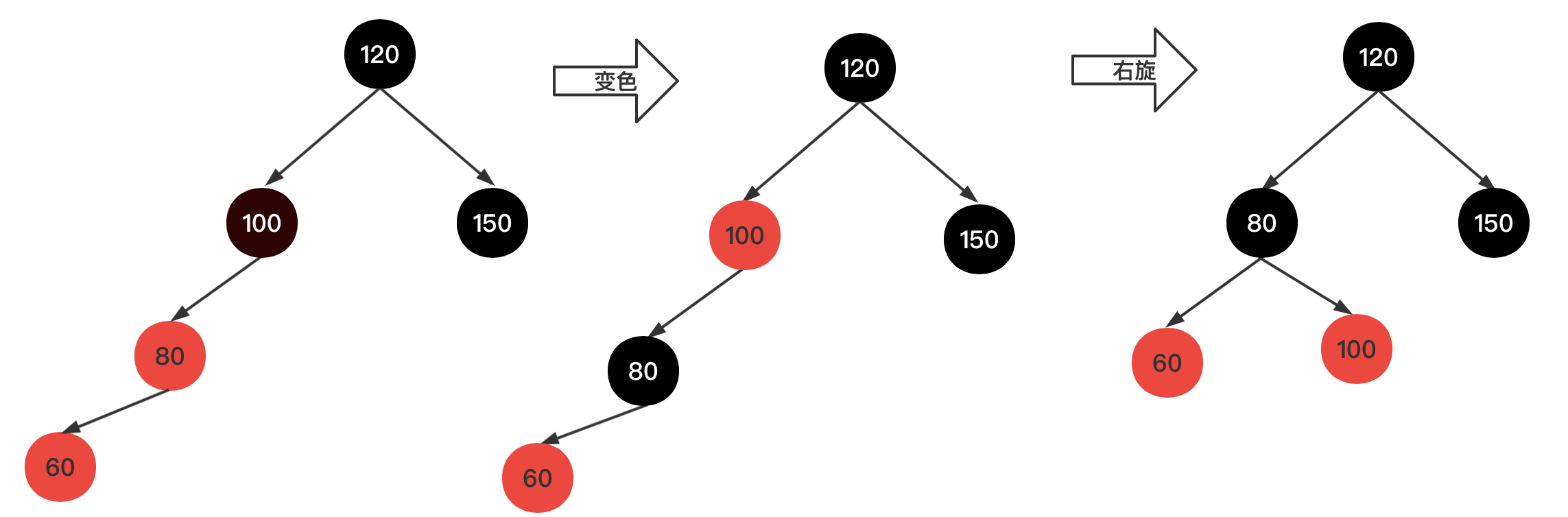
插入新红结点60，由于父结点80为黑色，进行变色操作，其中父结点变成黑色，爷结点变成红色，此时从节点100到左右两个叶子结点的黑色结点数量不一致，破坏第4规则，所以需要右旋操作

6、插入新结点，值为40，如下图示

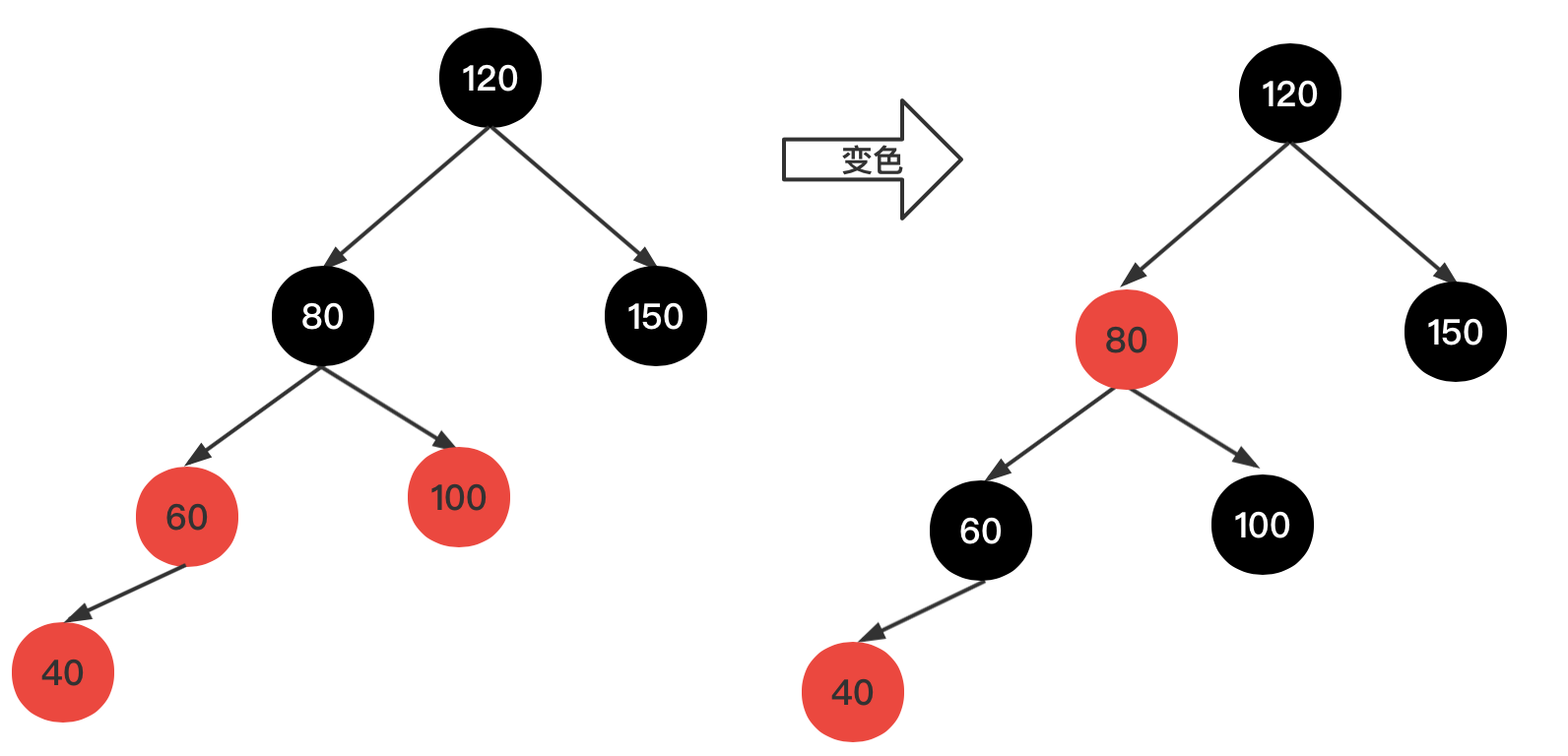
插入新红结点40，由于父结点为红色的，进行变色操作，将父结点60和叔结点100变成黑色，爷结点80变成红色

7、插入新结点，值为50，如下图示

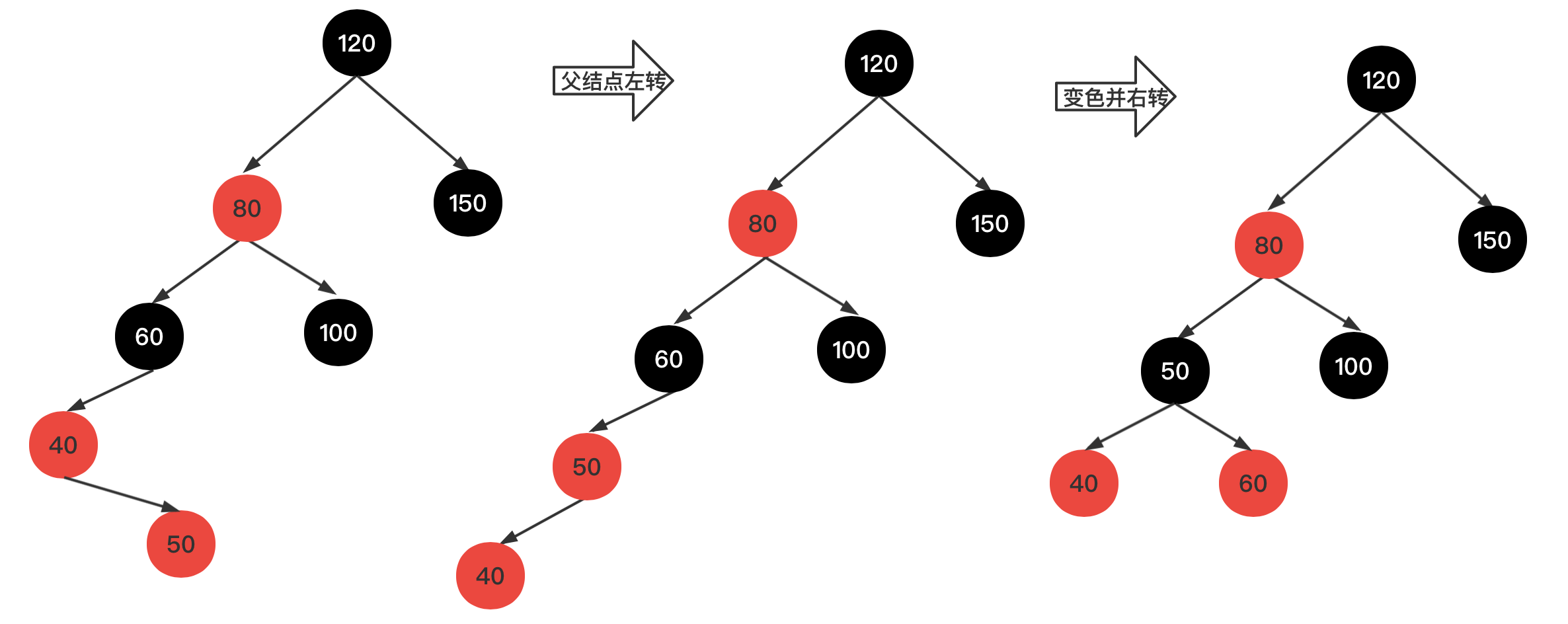
插入新红结点50，由于父结点为红色，破坏第4原则，将该结点的父结点进行左转操作，此时新结点和父结点互换身份，此时结点40当作是新结点，由于父结点50为红色，则将父结点50和爷结点60变色处理，并且对爷结点60进行右转操作。

8、插入新结点，值为70，如下图示

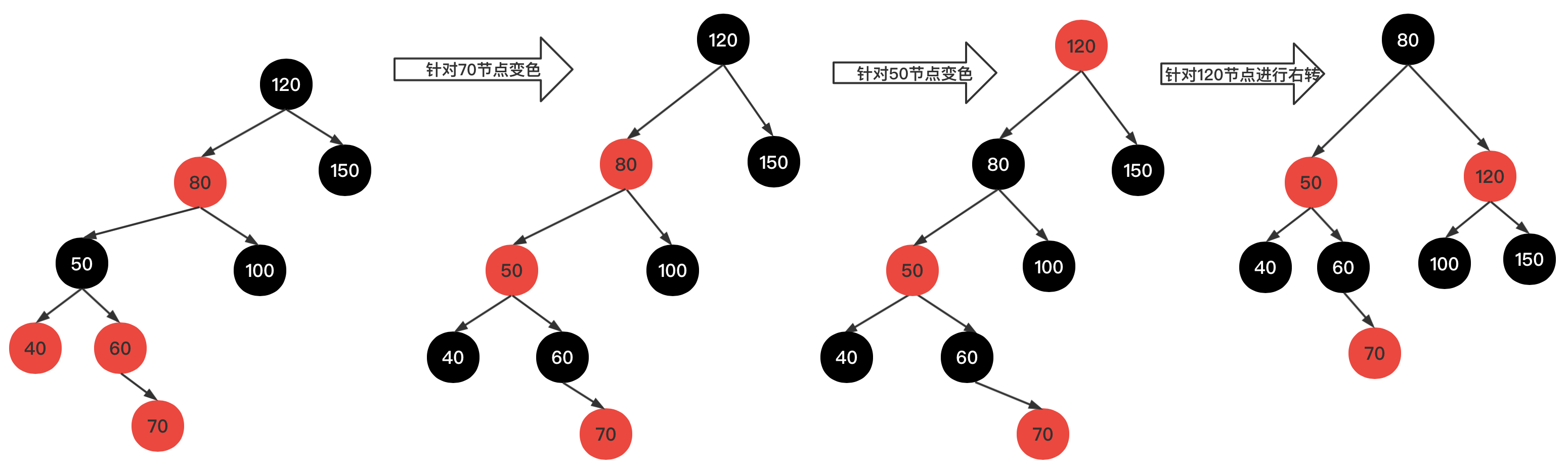
插入新红结点70，父结点为红结点，破坏第4原则，进行变色处理，并将爷结点50作为新插入点递归判断，针对50结点变色父结点80和爷爷结点120，然后针对120结点进行一次右转操作

 红黑树的变色旋转规则其实很简单，但是实际还是需要自行操作，尝试模拟红黑树的变色旋转流程才能彻底掌握。

4、红黑树删除结点

相对于插入结点，红黑树删除结点的流程要比插入流程复杂的多，插入流程分为插入和平衡两步，插入的过程比较简单，就是从根结点依次判断，直到找到需要插入的位置直接插入即可，然后就开始进行变色旋转等平衡操作。而红黑树的删除结点和插入类似，也分成删除结点和删除平衡两步

4.1、红黑树删除结点

红黑树的删除操作主要分成几种情况，以下将需要删除的结点简称为（删点）

1、删点没有子结点，则再分成两种情况

1.1、删点是红结点，不会破坏红黑树原则，直接删除即可,如下图示

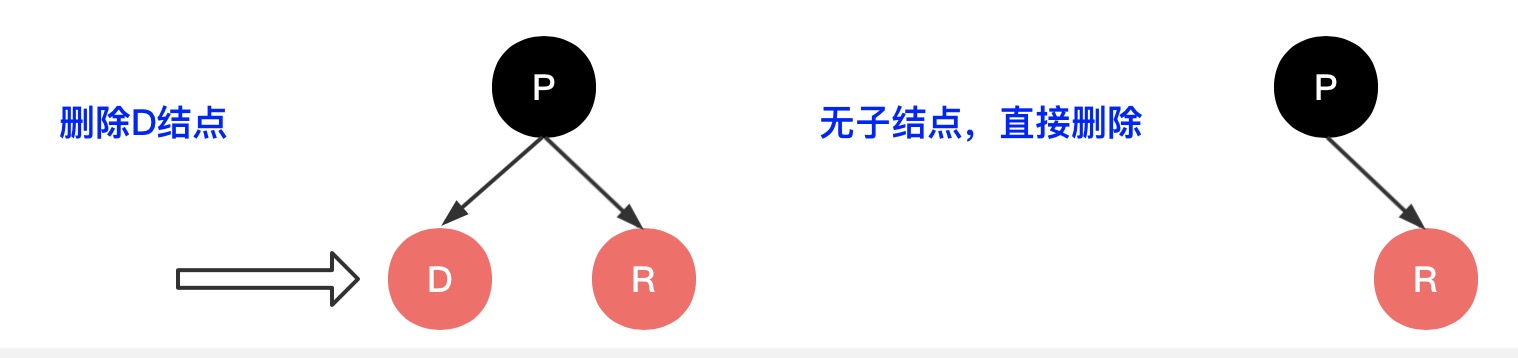
1.2、删点是黑结点，则此结点肯定有兄弟结点，有可能是黑色也有可能是红色，此时删除之后会造成红黑树不平衡，所以先直接删除，然后再走4.2的删除平衡操作如下图示

2、删点有一个子结点，则可以得出结论子结点肯定是红色，且删点必然是黑色，此时将子结点和删点位置互换，然后将删点直接删除，然后再走4.2的删除平衡操作，如下图示

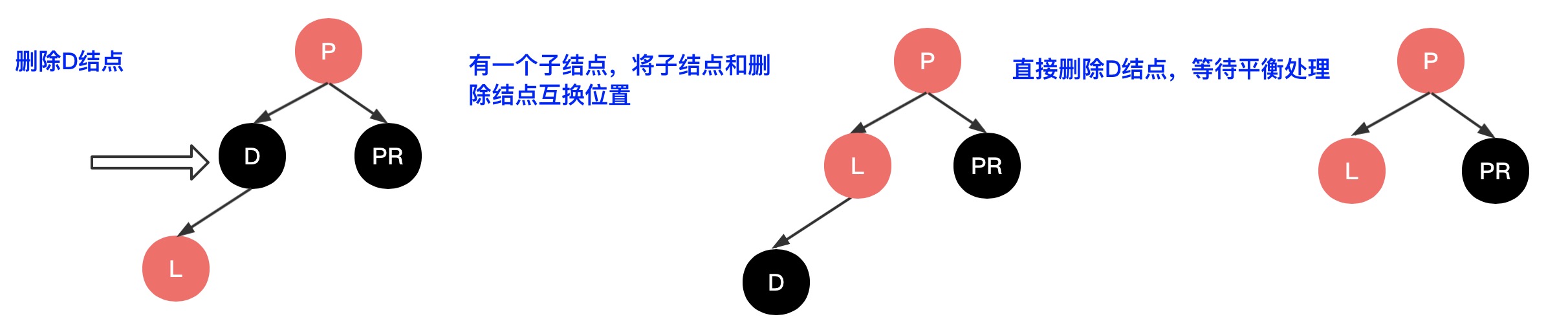
3、删点有两个子结点，那么先找到删点的后继结点（比删点的值小的最大一个结点，比如删点值为100，下面的子结点和孙子结点为80、90、110、120）则后继结点为90

将后继结点和删点的位置互换，然后将删点继续从第1步开始走删除流程，直到满足以上三种可以直接删除的条件，最后再走删除平衡操作，如下图示

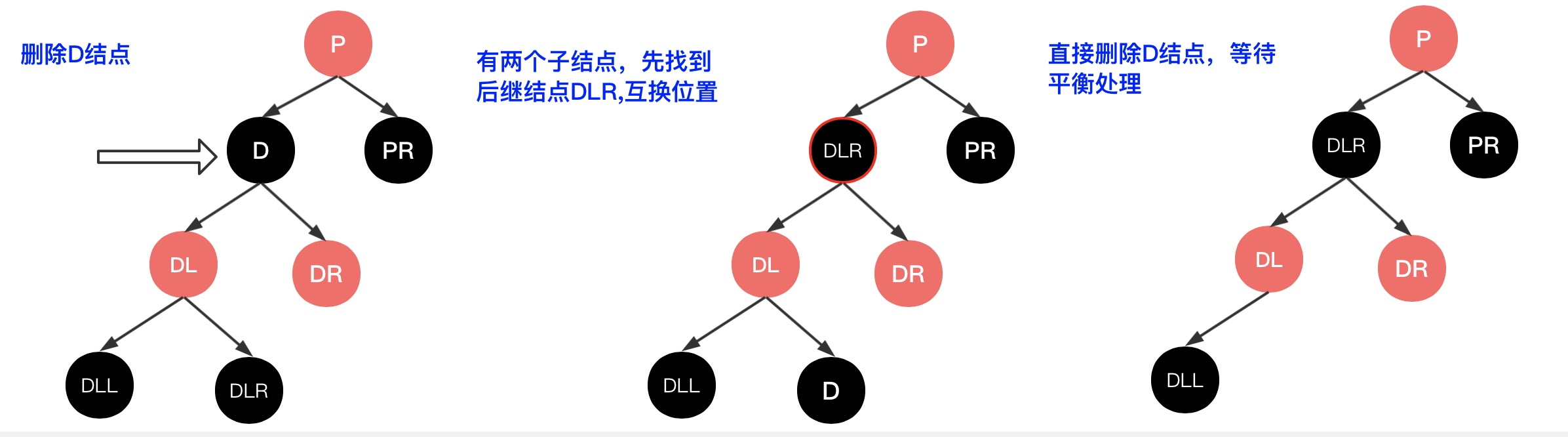
4.2、红黑树删除平衡

通过4.1可以将需要删除的结点删除掉，但是删除掉之后会破坏了红黑树的平衡，所以需要针对删除之后进行一次平衡操作。从4.1可知主要有以下其中情况需要进行删除平衡操作

1、删除结点无子结点，且为黑结点，此时兄弟结点分支的黑结点数必然多余被删除结点的分支

2、删除结点有一个子结点，子结点必然为红色，被删结点必然为黑色，需要平衡处理

3、删除结点有两个子结点，则需要递归判断，如果被删的是黑色结点，则必然需要进行平衡处理

其实就可以总结一句话：当被删结点为黑结点时，若不是根结点，则就必须进行平衡处理。

具体的平衡规则如下：

定义变量X为基点

 1、递归判断

 2、如果基点为空或者为根结点,平衡结束

 3、如果基点的父结点为空,则将基点变成黑色,平衡结束

 4、如果基点是红结点,将基点变成黑结点,平衡结束

 5、如果基点为黑色结点,且肯定存在父结点时,走以下逻辑

 5.1、如果基点是父结点左子结点

 5.1.1、如果基点存在兄弟结点(父结点的右子结点),且兄弟结点为红结点,则将兄弟结点变成黑结点,将父结点变成红结点,并且针对父结点进行一次左旋操作

 5.1.2、如果基点不存在兄弟结点,则将父结点当作基点重新从第1步开始执行递归判断

 5.1.3、如果基点存在兄弟结点,且兄弟结点为黑色,则分成以下几种情况

 5.1.3.1、如果兄弟结点没有红色子结点时,将兄弟结点变成红色,将父结点当作基点从第1步开始执行递归判断

 5.1.3.2、如果兄弟结点没有结点或者至少有一个红色子结点时,走以下逻辑:

 5.1.3.2.1、当兄弟结点的右子结点不为红结点时(表示左子结点为红或左子结点不存在),则将左子结点变成黑,并且将兄弟结点变成红色,则针对兄弟结点进行一次右旋操作

 5.1.3.2.2、如果兄弟结点存在,如果父结点不存在则变色为黑色;否则变色为和父结点同色(同色必然是黑色),并且将兄弟结点的右子结点变色为黑色

 5.1.3.2.3、如果父结点不为空,变色为黑色,并且将父结点做一次左转操作

 5.1.4、将根结点赋值给x,根据第2步得知,当x为根结点时,平衡结束

 5.2、如果基点是父结点右子结点
 (执行和5.1逻辑完全相反的逻辑)

总结：

1、当删除结点为根结点或者为红色结点时，不做任何平衡处理

2、当删除结点为黑结点，且不存在兄弟结点时，将父结点作为删除点重新判断

3、当删除结点为黑结点，且兄弟结点为红结点，则将兄弟结点变成黑色，父结点变成红色，针对父结点进行一次左旋操作，如下图2

4、当删除结点为黑结点，且兄弟结点为黑结点，且兄弟结点没有红色子结点时(无结点、或一个黑子结点、或两个黑子结点)，将兄弟结点变成红色，将父结点作为删除点重新判断

5.1、当删除结点为黑结点，且兄弟结点为黑结点，且兄弟结点有一个红结点，分下面两种情况

   5.1.1、红色子结点方向和删除结点的方向不同(一个为左结点一个为右结点)时， 

   5.1.2、红色子结点方向和删除结点的方向相同(同为左结点或同为右结点)时，则先将兄弟结点变红,兄弟结点的子结点变黑，然后将兄弟结点旋转(兄弟结点是左结点就是左旋，是右结点就右旋)

5.2、当删除结点为黑结点，且兄弟结点为黑结点，且兄弟结点有两个红结点

5.3、当删除结点为黑结点，且兄弟结点为黑结点，且兄弟结点有一个红结点和一个黑结点

接下来针对上面的删除结点的情况，根据平衡规则分别进行如下操作：

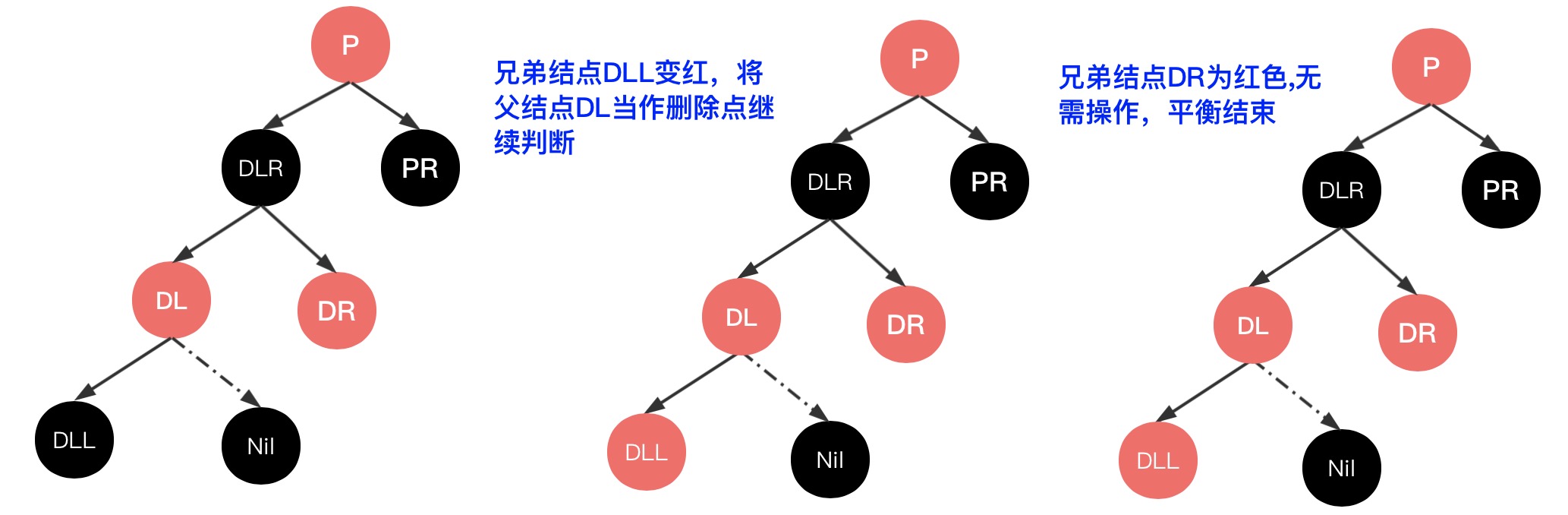
例子1.2、删除结点有兄弟结点，但是兄弟结点没有红色子结点，则将兄弟结点变红色，则将父结点当作删除点重新判断；由于父结点就是根结点，所以平衡结束

 

例子2、删点有一个红色子结点，删除之后和子结点互换位置删除，则此时子结点为红色，兄弟结点为黑色，但是兄弟结点没有红色子结点，所以和例子1.2平衡逻辑一样，将兄弟变成红色即可，然后将父结点当作删除点继续判断，父结点变成黑色；

例子3、删除点有一个无子结点的黑色兄弟结点DLL，将黑色兄弟结点变色，然后将父结点DL当作删除点继续判断；