一、概念
查找表(Search Table)是由同一类型的数据元素构成的集合,它是一种以查找为“核 心”,同时包括其他运算的非常灵活的数据结构。
查找就是从大量的数据元素中找出某个指定的数据元素。关键字分为主关键字和次关 键字两种。前者可以唯一标识一个数据元素,即对于不同的数据元素其主关键字均不同; 后者则可以识别若干数据元素。
静态查找表是以具有相同特性的数据元素集合为逻辑结构,包括下列三种基本运算 :建表 Create(ST)、查找 Search(ST, key)、 读表中元素 Get(ST, pos)
动态查找表是以集合为逻辑结构,包括下列五种基本运算: 初始化 Initiate (ST)、查找 Search(ST,key)、读表中元素 Get(ST, pos)、 插入 Insert(ST,key)、 删除 Delete(ST,key)。、
二、静态查找表
1、顺序查找
从表中 最后一个 记录开始 顺序 进行查找,若当前记录的关键字= 给定值,则 查找成功 ;否则,继续查上一记录…;若直至第一个记录尚未找到需要的记录,则 查找失败
//使用一种 设计技巧 :设立 岗哨 int SearchSqtable(Sqtable T, KeyType key){ /* 在顺序表R 中顺序查找其关键字等于key 的元素。 若找到,则函数值为该元素在表中的位置,否则为0*/ T.elem[0].key=key; //设置岗哨 i=T.n;//设置比较位置初值 while ( T.elem[i].key!=key ){ i-- } return i ; }
查找成功:最少1次、最多 n+1次 、 平均查找长度=(n+1)/2
查找失败:n+1次
例如:假设顺序表的(b1,b2,b3)的概率是0.2,0.2,0.6,顺序查找的平均长度?
ASL=0.2*(3-1+1)+0.2(3-2+1)+0.6(3-3+1)=1.6
时间复杂度:n
2、有序表上的查找—二分查找
二分查找基本思想: 每次将处于查找区间中间位置上的数据元素与给定值K 比较,若不等则缩小查找区间并在新的区间内重复上述过程,直到查找成功或查找区间长度为0 (查找不成功)为止
有序表:如果顺序表中数据元素是按照键值大小的顺序排列的,则称为有序表。
算法过程:
- 1、用给定值 key 与处在中间位置的数据元素 T.elem[mid]的键值 T.elem[mid] .key 进行 比较,可根据三种比较结果区分三种情况:
- 2、key=T.elem[mid].key,查找成功,T.elemEmid]即为待查元素;
- 3、key<t.elem[mid].key,说明若待查元素若在表中,则一定排在 t.elem[mid]="" 之前;
- 4、key>T.elem[mid].key,说明若待查元素若在表中,则一定排在 T.elem[mid]之后。
/*在有序表 T 中,用二分查找法查找键值等于 key 的元素,变量 low,hig 分别标记查找 区间的下界和上界*/ int SearchBin{SqTable T,KeyType key){ int low,high; low=l;high=T.n; //置查找区间初值 while (low<=high){ //区间长度不为 0 时继续查找 mid= (low+high) /2; //对区间进行折半,〃/〃为整除 if (key==T.elem[mid].key){ return mid; } else if(key<T.elem[mid] .key){ high=mid-1; //在前半区间查找 } else { low=mid+1; //在后半区间查找 } } return 0; //查找不成功,则返回 }

时间复杂度:log2n
3、索引顺序表上的查找-分块查找
索引顺序表是结合了顺序查找和二分查找的优点构造的一种带索引的存储结构
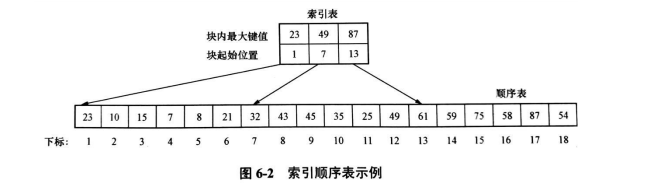
一个索引顺序表由两部分组成:一个索引表和一个顺序表。其中的顺序表在组织形式上 与普通的顺序表完全相同,而索引表本身在组织形式上也是一个顺序表。索引表通过索引将 顺序表分割为若干块,而顺序表呈现出“按块有序”的性质。
若静态查找表用索引顺序表表示,则查找操作可用分块查找来实现,也称为索引顺序查 找。根据上面对索引顺序表的描述,在索引顺序表上的查找即分块查找分两步进行:先确定 待查数据元素所在的块;然后在块内顺序查找。

二、动态查找表
1、二叉排序树上的查找
二叉排序树:一种实现动态查找的树表——二叉排序树,这种树表的结构本身是在查找过程中动态 生成的,即对于给定 key,若表中存在与 key 相等的元素,则查找成功,不然,插入关键字 等于 key 的元素。 一棵二叉排序树(Binary Sort Tree)(又称二叉查找树)或者是一棵空二叉树,或者是具有下列性质的二叉树:
- (1) 若它的左子树不空,则左子树上所有结点的键值均小于它的根结点键值;
- (2) 若它的右子树不空,则右子树上所有结点的键值均大于它的根结点键值;
- (3) 根的左、右子树也分别为二叉排序树。

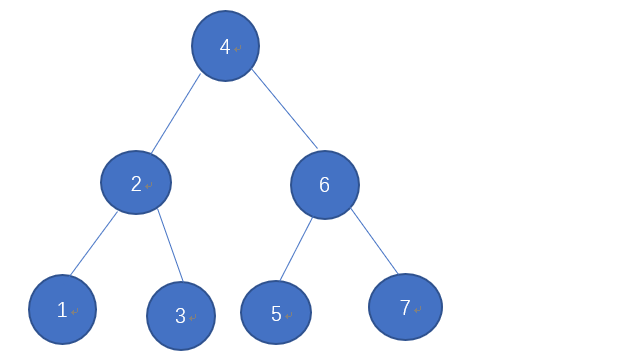
中序遍历一棵二叉排序树所得的结点访问序列是键值的递增序列:1,2,3,4,5,6,7
在二叉排序树上进行插入的原则是:必须要保证插入一个新结点后,仍为一棵二叉排序 树。这个结点是查找不成功时查找路径上访问的最后一个结点的左孩子或右孩子。
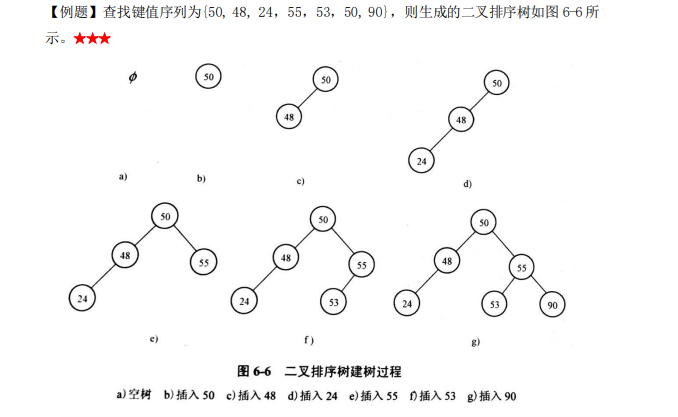
二叉排序树的查找分析:二叉排序树上的平均查找长度是介于O(n)和O(log 2 n)之间的,其查找效率与树的形态(树的生成过程)有关
二叉排序树的平均查找长度:O(log 2 n) ;最坏情况下单支树 平均查找长度:ASL=(n+1)/2;
二叉树的查找长度不仅与节点的数量有关,还与二叉排序树的生产过程有关
由n个键值构造的二叉排序树,在等概率查找的假设下,查找成功的平均查找长度的最大值可能达到 (n+1)/2

2、散列表
散列函数:数据元素的键值和存储位置 T 之间建立的对应关系 H 称为散列函数,用键值通过散列函数获取存储位置的这种存储方式构造的存储结构称为散列表,这一映射过程称为散列或哈希造表。所得存储位置称散列地址或哈希地址。
散列表进行查找的基本出发点是:减少查找过程中的比较次数

散列地址—— 由散列函数决定数据元素的存储位置,该位置称为散列地址。
散列表—— 通过散列法建立的表称为散列表
常用散列法
若对于键值集合中的任一个键值,经散列函数映射到地址集合中任何一个地址的概率是相等的,则称此种散列函数是均匀的。
- 1、数字分析法
- 2、除留余数法:除留余数法是一种简单有效且最常用的构造方法,其方法是选择一个不大于散列表长n的正整数p,以键值除以p所得的余数作为散列地址,即H(key)=key mod p(p≤n)注意:通常选 p 为小于散列表长度 n 的素数。
- 3、平方取中法
- 4、基数转换法
质数又称为素数,是一个大于1的自然数,除了1和它自身外,不能被其他自然数整除的数叫做质数
散列法主要工作
- 选择一个好的散列函数:函数计算简便,运算速度快;随机性好,地址尽可能均匀分布;冲突小
- 解决冲突
散列表的实现
通常用来解决冲突的方法有以下几种:
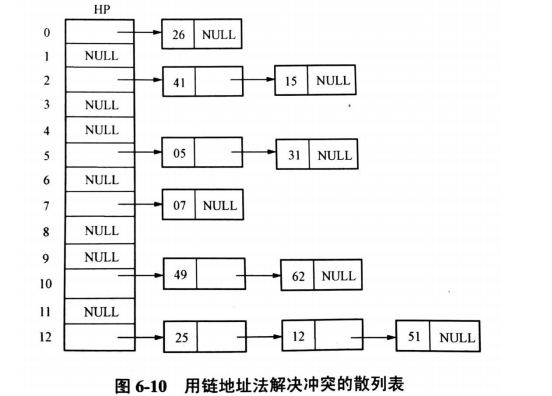
1、链地址法:避免冲突
思想:将散列地址相同记录存储在同一单链表中(称同义词表),同时按散列地址设立一个表头指针向量。
例如,若选定的散列函数为H(key)=key mod 13,已存入键值为 26,41,25,05, 07,15,12, 49, 51, 31, 62 散列表。