隐马尔可夫模型（四）——隐马尔可夫模型的评估问题(后向算法）（转载）

对于HMM的评估问题，利用动态规划可以用前向算法，从前到后算出前向变量；也可以采用后向算法，从后到前算出后向变量。

先介绍后向变量β_t(i):给定模型μ=（A,B,π），并且在时间 时刻t 状态为s_i 的前提下，输出序列为O_t+1O_t+2...O_T的概率，即

                                    β_t(i)=P(O_t+1O_t+2...O_T|q_t=s_i,μ)

归纳过程

    假设仍然有3个状态

                  

    当t=T时，按照定义：时间t  状态q_T 输出为O_T+1......的概率，从T+1开始的输出是不存在的（因为T时刻是终止终止状态），即T之后是空，是个必然事件，因此β_t(i)=1,1≤1≤N

    当t=T-1时，

                          

                 β_T-1(i)=P(O_T|q_T-1=s_i,μ) = a_i1*b₁（O_T)*β_T(1)  +  a_i2*b₂（O_T)*β_T(2)  +  a_i3*b₃（O_T)*β_T(3)

      ......

    当t=1时，

       β₁(1)=P(O₂O_3...O_T|q₂=s₁,μ) = a₁₁*b₁（O₂)*β₂(1) + a₁₂*b₂（O₂)*β₂(2) + a₁₃*b₃（O₂)*β₂(3)

       β₁(2)=P(O₂O_3...O_T|q₂=s₁,μ) = a₂₁*b₁（O₂)*β₂(1) + a₂₂*b₂（O₂)*β₂(2) + a₂₃*b₃（O₂)*β₂(3)

       β₁(3)=P(O₂O_3...O_T|q₂=s₁,μ) = a₃₁*b₁（O₂)*β₂(1) + a₃₂*b₂（O₂)*β₂(2) + a₃₃*b₃（O₂)*β₂(3)

       P(O₁O₂...O_T|μ) =    

                             =   

                             =  

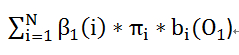
后向算法

    step1 初始化：β_T(i)=1, 1≤1≤N

    step2 归纳计算：

                       1≤t≤T-1, 1≤i≤N

    step3 求终结和：

                   P(O|μ）=  

时间复杂度

    计算某时刻在某个状态下的后向变量需要看后一时刻的N个状态，此时时间复杂度为O(N),每个时刻有N个状态，此时时间复杂度为N*O(N)=O(N²),又有T个时刻，所以时间复杂度为T*O(N²)=O(N²T)。

程序例证

              

后向算法

    计算P(O|M)：

    step1：β₄(1) = 1          β₄(2) = 1          β₄(3) = 1

    step2：β₃(1) = β₄(1)*a₁₁*b₁(white) + β₄(2)*a₁₂*b₂(white) + β₄(3)*a₁₃*b₃(white)

                     ...

    step3:P(O|M) = π₁*β₁(1)*b₁(O₁) + π₂*β₁(2)*b₂(O₁) + π₃*β₁(3)*b₃(O₁)

程序代码

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

int main()
{
        float a[3][3] = {{0.5,0.2,0.3},{0.3,0.5,0.2},{0.2,0.3,0.5}};
        float b[3][2] = {{0.5,0.5},{0.4,0.6},{0.7,0.3}};
        float result[4][3];
        int list[4] = {0,1,0,1};
        result[3][0] = 1;
        result[3][1] = 1;
        result[3][2] = 1;
        int i,j,k, count = 3;
        for (i=2; i>=0; i--)
        {
            for(j=0; j<=2; j++)
            {
                result[i][j] = 0;
                for(k=0; k<=2; k++)
                {
                   result[i][j] += result[i+1][k] * a[j][k] * b[k][list[count]];
                }
            }
            count -= 1;
        }
       for (i=0; i<=3; i++)
        {
            for(j=0; j<=2; j++)
            {
                printf("b[%d][%d] = %f
",i+1,j+1,result[i][j]);

            }
        }
        printf("backward:%f
", result[0][0]*0.2*0.5+result[0][1]*0.4*0.4+result[0][2]*0.4*0.7);
        return 0;
}

运行结果