AC自动机
AC自动机,说白了就是在trie树上跑kmp(其实个人感觉比kmp容易理解)。是一种多匹配串,单个主串的匹配。概括来说,就是将多个匹配串构造一个trie树,对于每个trie树的节点构造nxt指针,最后把主串放在上面跑。
构造trie树
和普通的trie树构建一样,没有什么区别
inline void insert(char *s){ int l=strlen(s); int u=1; REP(i,0,l-1){ int c=calc(s[i]); if(!tree[u][c]) tree[u][c]=++total; u=tree[u][c]; } isend[u]++;//注意isend的具体处理根据题目而定 return ; }
构造nxt数组
其实这一部分是AC自动机的核心,我们这样构造:对于每个节点,它的nxt是,它父亲的nxt的和它名字相同的儿子。如图,u的父亲是v,它父亲的nxt的a这个儿子就是u的nxt。
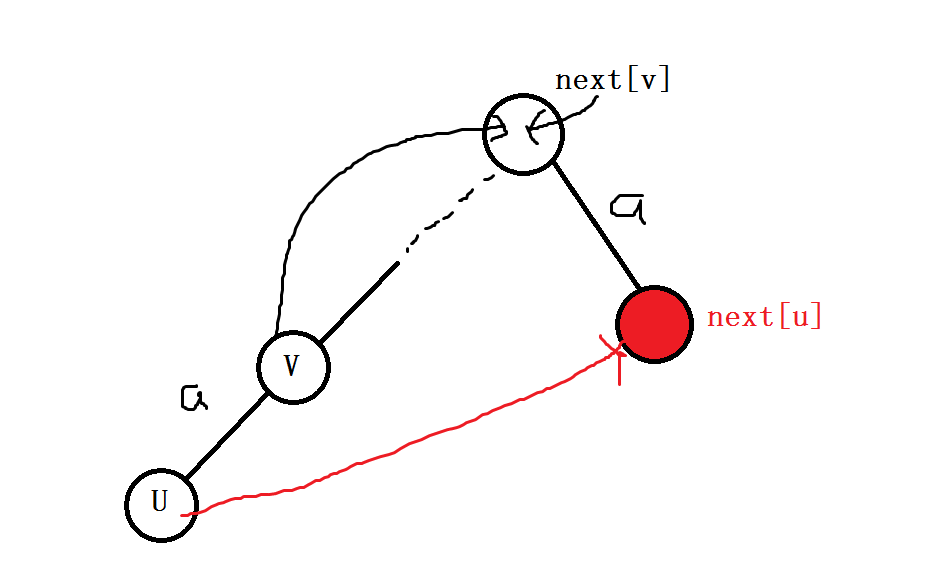
还有一种情况,就是如果节点u,它的没有a这个儿子,那么它就要把nxt[u]的a这个儿子当成他的儿子。
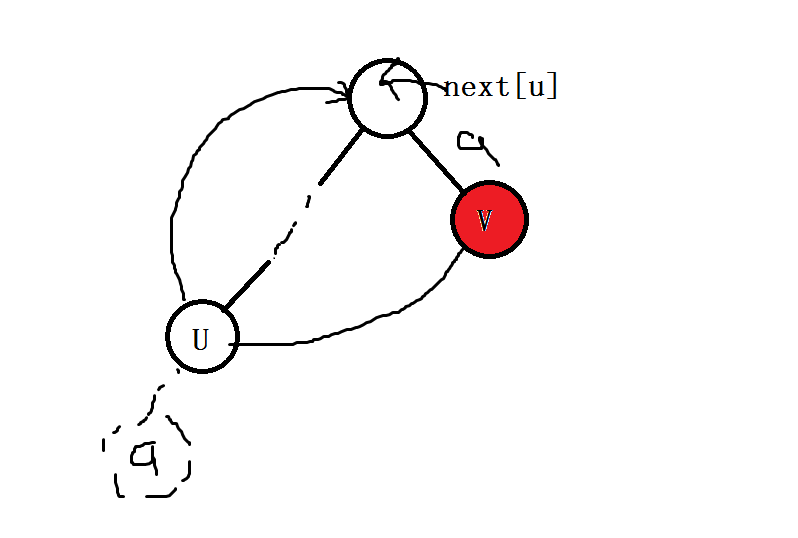
如图,因为u没有a的子节点,所以就连到nxt[u]的a子节点。
那么这么做的原因是什么?我们来看一下这个图:

如图,这个trie树中前7个节点的next都已经构造完成了(箭头表示他们的nxt,1的nxt是0,没有画出来).现在要找8的next。按照“它的nxt是,它父亲的nxt的和它名字相同的儿子”的原则,我们找到8的父亲,7,发现7的nxt,5也没有B这个儿子,这时候我们需要找5的next,2,最终发现2有B儿子,是4,将8连到4。
但是注意,其实我们这一个一个找nxt是可以省略的。如果按着刚才“因为u没有a的子节点,所以就连到nxt[u]的a子节点。”树就会变成这样(黑线表示连边,红线表示next)
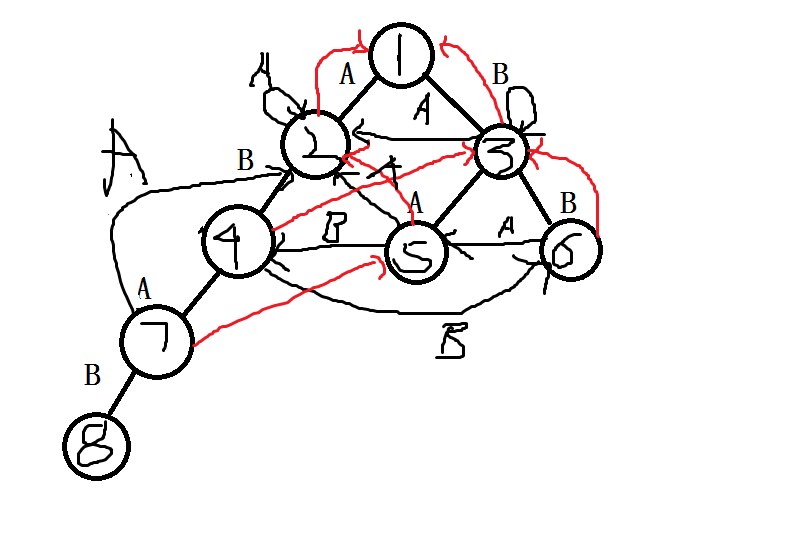
5因为没有B儿子,就把他的nxt:2,的B儿子:4,当成自己的儿子,7也同理,因为它没有A儿子,所以把他的nxt的A儿子:2,当成自己的A儿子。再来看8,发现它的父亲的nxt,5,的B儿子是4,所以自己的next就是4了。这样减少了刚才一个一个找nxt的步骤。
inline void getnxt(){//整个代码用BFS实现 while(!Q.empty()) Q.pop(); REP(i,0,25) tree[0][i]=1;//一个非常重要的细节处理,我们加一个虚拟节点0,并将它的所有边都连到1,方便以后的运算 nxt[1]=0; Q.push(1); while(!Q.empty()){ int u=Q.front();//u是当前点,这时候nxt[u]已经处理过了,要处理的是u的儿子的nxt,也就是nxt[tree[u][i]] Q.pop(); REP(i,0,25){//枚举u节点的每一个子节点 if(!tree[u][i]) tree[u][i]=tree[nxt[u]][i];//这就是刚才说的很重要的一步优化, 如果自己没有这个子节点,就把自己next的这个子节点当做自己的子节点。 else{ nxt[tree[u][i]]=tree[nxt[u]][i];//自己儿子的nxt等于自己nxt的儿子,这句话和“自己的nxt是,自己父亲的nxt的和它名字相同的儿子”的意思相同,只是主语从待更新节点变成已就更新节点。 Q.push(tree[u][i]); } } } return ; }
查找
查找的具体实现是根据题目而定,我就拿这道题举个例子:给一大堆匹配串和一个主串,求有多少个匹配串在主串上出现过。
这种题的做法就是现在构建trie树的时候,把每个单词的结尾都记录一下:isend[i]++。最后跑一遍AC自动机,到每一个节点是ans+=isend[i];isend=0;这样听起来很简单,那么怎么遍历AC自动机呢?
循环遍历主串s,令u表示当前点,每当主串s到下一位时,u=tree[u][s[i]-‘a’](就是等于它的儿子)。然后对于每个u,循环它的nxt直到根。每到一个点就ans+=isend。具体看代码:
inline void search(){ int ans=0; int u=1; int l=strlen(t); REP(i,0,l-1){//循环遍历主串 int c=calc(t[i]);//计算这个字符的ACCII码 int k=tree[u][c]; while(k>1){//对于每一个u遍历它的nxt,直到根 if(isend[k]){ ans+=isend[k];//加上isend,记录答案 isend[k]=0; } k=nxt[k]; } u=tree[u][c];//遍历到它的儿子。 } printf("%d ",ans); }
总结
再来回顾一下AC自动机的步骤:构建trie树,构建next数组,查找。其中next有两个原则:1、当这个节点没有字符c这个儿子时,把自己的next的c这个儿子当做自己的儿子
2、自己儿子的nxt等于自己nxt的儿子
附上代码:#include <iostream>
#include <cstdio> #include <algorithm> #include <cstring> #include <cmath> #include <cstdlib> #include <queue> #include <stack> #include <vector> using namespace std; #define MAXN 100010 #define INF 10000009 #define MOD 10000007 #define LL long long #define in(a) a=read() #define REP(i,k,n) for(int i=k;i<=n;i++) #define DREP(i,k,n) for(int i=k;i>=n;i--) #define cl(a) memset(a,0,sizeof(a)) inline int read(){ int x=0,f=1;char ch=getchar(); for(;!isdigit(ch);ch=getchar()) if(ch=='-') f=-1; for(;isdigit(ch);ch=getchar()) x=x*10+ch-'0'; return x*f; } inline void out(int x){ if(x<0) putchar('-'),x=-x; if(x>9) out(x/10); putchar(x%10+'0'); } int T,n; int total=1; int nxt[1000010],tree[500010][26]; char in[55]; int isend[1000010]; char t[1000010]; queue <int> Q; int calc(char c){ return c-'a'; } inline void insert(char *s){ int l=strlen(s); int u=1; REP(i,0,l-1){ int c=calc(s[i]); if(!tree[u][c]) tree[u][c]=++total; u=tree[u][c]; } isend[u]++; return ; } inline void getnxt(){//整个代码用BFS实现 while(!Q.empty()) Q.pop(); REP(i,0,25) tree[0][i]=1;//一个非常重要的细节处理,我们加一个虚拟节点0,并将它的所有边都连到1,方便以后的运算 nxt[1]=0; Q.push(1); while(!Q.empty()){ int u=Q.front();//u是当前点,这时候nxt[u]已经处理过了,要处理的是u的儿子的nxt,也就是nxt[tree[u][i]] Q.pop(); REP(i,0,25){//枚举u节点的每一个子节点 if(!tree[u][i]) tree[u][i]=tree[nxt[u]][i];//这就是刚才说的很重要的一步优化, 如果自己没有这个子节点,就把自己next的这个子节点当做自己的子节点。 else{ nxt[tree[u][i]]=tree[nxt[u]][i];//自己儿子的nxt等于自己nxt的儿子,这句话和“自己的nxt是,自己父亲的nxt的和它名字相同的儿子”的意思相同,只是主语从待更新节点变成已就更新节点。 Q.push(tree[u][i]); } } } return ; } inline void search(){ int ans=0; int u=1; int l=strlen(t); REP(i,0,l-1){//循环遍历主串 int c=calc(t[i]);//计算这个字符的ACCII码 int k=tree[u][c]; while(k>1){//对于每一个u遍历它的nxt,直到根 if(isend[k]){ ans+=isend[k];//加上isend,记录答案 isend[k]=0; } k=nxt[k]; } u=tree[u][c];//遍历到它的儿子。 } printf("%d ",ans); } int main(){ in(T); while(T--){ total=1; cl(nxt); cl(tree); cl(isend); in(n); REP(i,1,n){ scanf("%s",in); insert(in); } scanf("%s",t); getnxt(); search(); } return 0; }
附加:可持久化AC自动机
如果你希望每当你查找到一个字符串,然后要把它删去时,就需要可持久化AC自动机。其实和普通的AC自动机很像,唯一区别是查找的时候去掉了对于每一个u遍历nxt直到根的步骤,然后让每个u都压进栈,遇到end就弹出栈里面此字符串长度的元素。