动态开点线段树
前置芝士
众所周知,普通线段树空间复杂度是 (O(n*4))
所以当n很大的时候,如果正常的去建一颗线段树,开4倍n空间显然会炸内存
怎么办呢?
这个时候,动态开点线段树出现了。
概念
动态开点线段树是一类特殊的线段树,与普通的线段树不同的是,每一个节点的左右儿子不是该点编号的两倍和两倍加一,而是现加出来的。
简单的说,就是建立一棵“残疾”的线段树,上面只有询问过的相关节点。
大概长这样(借的图,自己画的太丑了),理解即可,写出来的可能不长这样
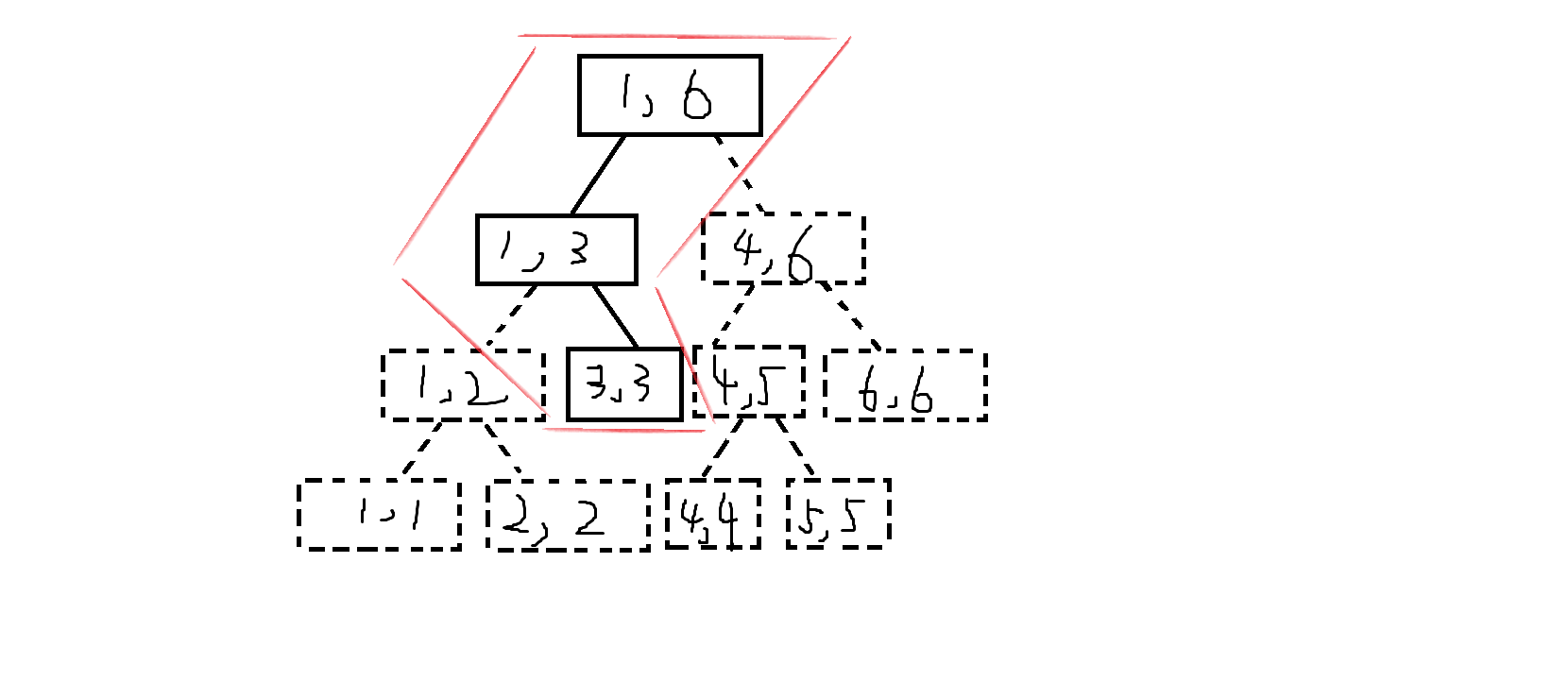
作用
一般有两种:
- 节约空间,所以在需要时再建儿子。
- 运用主席树的时候(此文章不会提及)。
代码
更新
inline void push_up(int o){
sum[o]=sum[ls[o]]+sum[rs[o]];
}
ls[o],rs[o]代表lson和rson,以下都一样
插入
inline void update(int &o,int l,int r,int pos,int val){ //o为当前树的编号 l r为区间 pos为插入位置 val为插入大小
if(!o) o=++cnt;//开点
if(l==r){
sum[o]+=val;
return ;
}
int mid=(l+r)>>1;
if(x<=mid) update(ls[o],l,mid,pos,val);
else update(rs[o],mid+1,r,pos,val);
push_up(o);//更新
}
查询
inline int ask(int o,int l,int r,int L,int R){
if(!o) return 0;//没有这个点,直接返回0
if(L<=l&&r<=R) return sum[o];
int val,mid=(l+r)>>1;
if(L<=mid) val+=ask(ls[o],l,mid,L,R);
if(R>mid) val+=ask(rs[o],mid+1,r,L,R);
return val;
}
和普通线段树一样,可维护的东西很多,在这里就不一一枚举了,读者自行理解。
提示
- 这个参数变量pos前面的取址符&是不能省略的,因为这个编号是不随递归修改的定值
- 时间复杂度 (O(dfrac{q}{logn})~~~~q) 为查询次数,(n) 为值域
例题
P1908 逆序对
题意
就是求一个序列的逆序对个数
思路
相信大家都做过这题,所以就不说思路了,只是把归并排序改为了动态开点线段树
代码
有注释的
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define lson l,mid,tree[rt].l
#define rson mid+1,r,tree[rt].r
#define ls tree[rt].l
#define rs tree[rt].r
const int mac=5e5+10;
const int inf=1e9+5;
struct node
{
int l,r,sum;
}tree[mac*32];
int sz=1;//动态分配的点的最大编号
ll query(int l,int r,int rt,int L,int R)
{
ll ans=0;
if (l>=L && r<=R){
return tree[rt].sum;
}
int mid=(l+r)>>1;
if (mid>=L) ans+=query(lson,L,R);
if (mid<R) ans+=query(rson,L,R);
return ans;
}
void update(int l,int r,int &rt,int pos)
{
if (!rt) rt = ++sz;//如果说这个节点不存在,我们就将节点数+1,当前节点为最大最大节点,和主席树有点类似,而这也是动态开点的核心
if (l==r) {
tree[rt].sum++;
return;
}
int mid=(l+r)>>1;
if (mid>=pos) update(lson,pos);//注意这里传进去的rt是左儿子的编号
else update(rson,pos);
tree[rt].sum=tree[ls].sum+tree[rs].sum;
}
int main()
{
int n;
scanf ("%d",&n);
ll ans=0;
int root=1;
for (int i=1; i<=n; i++){
int x;
scanf ("%d",&x);
ans+=query(1,inf,1,x+1,inf);
update(1,inf,root,x);
}
printf ("%lld
",ans);
return 0;
}
有问题请评论